Correzione della continuità di yate: definizione ed esempio

Un test di indipendenza chi quadrato viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.

Questo test utilizza le seguenti ipotesi nulle e alternative:

• H ₀ : (ipotesi nulla) Le due variabili sono indipendenti.
• H ₁ : (ipotesi alternativa) Le due variabili non sono indipendenti. (cioè sono associati)

Usiamo la seguente formula per calcolare la statistica del test Chi-quadrato x ² per questo test:

^X2 = Σ(O _i -E _i ) ² / E _i

Oro:

• Σ: è un simbolo di fantasia che significa “somma”
• O: valore osservato
• E: valore atteso

Questo test presuppone che le probabilità discrete delle frequenze in una tabella di contingenza possano essere approssimate dalla distribuzione Chi-quadrato, che è una distribuzione continua.

Tuttavia, questa ipotesi tende ad essere leggermente errata e le statistiche dei test risultanti tendono ad essere distorte al rialzo.

Per correggere questo errore, possiamo applicare la correzione di continuità di Yate , che applica la seguente correzione alla formula ^X2 :

X ² = Σ(|O _i -E _i | – 0,5) ² / E _i

Generalmente utilizziamo questa correzione solo quando almeno una cella nella tabella di contingenza ha una frequenza prevista inferiore a 5.

Esempio: applicazione della correzione di continuità di Yate

Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 40 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:

Ecco come eseguire un test di indipendenza chi quadrato con la correzione di continuità di Yate:

Valori osservati:

Valori attesi:

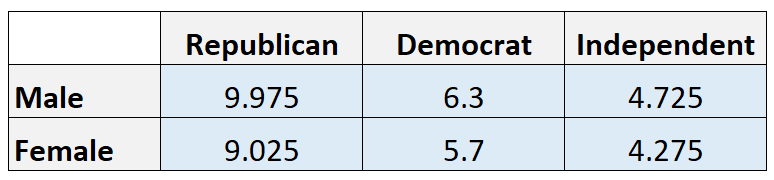
Nota: calcoliamo il valore atteso in ciascuna cella moltiplicando il totale della riga per il totale della colonna e quindi dividendo per il totale generale. Ad esempio, il numero atteso di uomini repubblicani è (21*19)/40 = 9.975.

_{Statistica del test} ^{Chi –} _quadrato :

• (|8-9,975| – 0,5) ² / 9,975 = 0,218
• (|9-6,3| – 0,5) ² / 6,3 = 0,768
• (|4-4,725| – 0,5) ² / 4,725 = 0,011
• (|11-9,025| – 0,5) ² / 9,025 = 0,241
• (|3-5,7| – 0,5) ² / 5,7 = 0,849
• (|5-4,275| – 0,5) ² / 4,275 = 0,012

^Quindi ,

Valore P: secondo il calcolatore chi quadrato/valore P , il valore p che corrisponde a una statistica test chi quadrato con 2 gradi di libertà è 0,3501 .

Poiché questo valore p non è inferiore a 0,05, non riusciremo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che esista un’associazione tra le preferenze di genere e quelle dei partiti politici.