Come eseguire un test di cramer-von mises in r (con esempi)

Il test di Cramer-Von Mises viene utilizzato per determinare se un campione proviene o meno da una distribuzione normale .

Questo tipo di test è utile per determinare se un determinato set di dati proviene o meno da una distribuzione normale, che è un presupposto comunemente utilizzato in molti test statistici, tra cui regressione , ANOVA , test t e molti altri. ‘altri.

Possiamo eseguire facilmente un test di Cramer-Von Mises utilizzando la funzione cvm.test() dal pacchetto goftest in R.

L’esempio seguente mostra come utilizzare questa funzione nella pratica.

Esempio 1: test di Cramer-Von Mises su dati normali

Il codice seguente mostra come eseguire un test di Cramer-Von Mises su un set di dati con dimensione del campione n=100:

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 0.078666, p-value = 0.7007

Il valore p del test risulta essere 0,7007 .

Poiché questo valore non è inferiore a 0,05, possiamo supporre che i dati del campione provengano da una popolazione distribuita normalmente.

Questo risultato non dovrebbe sorprendere poiché abbiamo generato i dati di esempio utilizzando la funzione rnorm() , che genera valori casuali da una distribuzione normale standard .

Correlato: Una guida a dnorm, pnorm, qnorm e rnorm in R

Possiamo anche produrre un istogramma per verificare visivamente che i dati del campione siano distribuiti normalmente:

 hist(data, col=' steelblue ') 

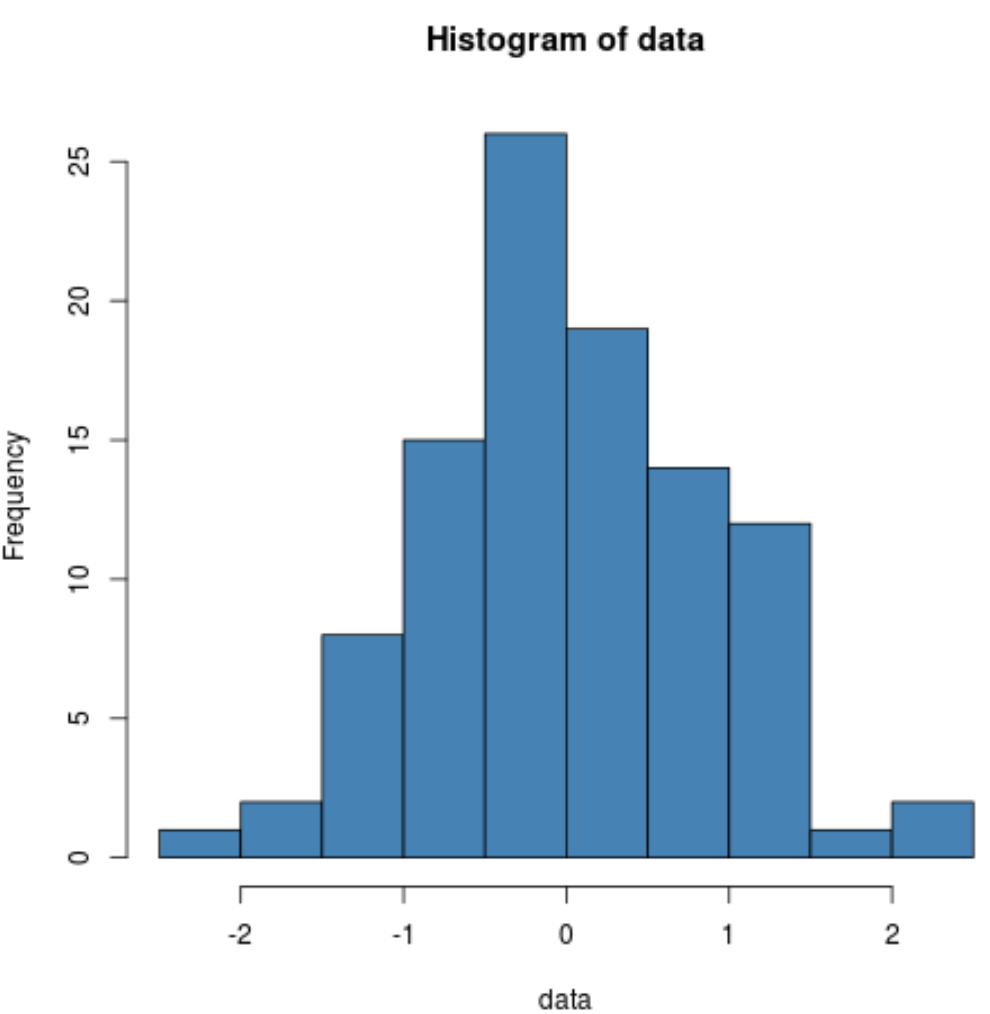
Possiamo vedere che la distribuzione è piuttosto a campana con un picco al centro della distribuzione, tipico dei dati distribuiti normalmente.

Esempio 2: test di Cramer-Von Mises su dati non normali

Il codice seguente mostra come eseguire un test di Cramer-Von Mises su un set di dati con una dimensione campionaria pari a 100 in cui i valori sono generati casualmente da una distribuzione di Poisson :

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 27.96, p-value < 2.2e-16

Il valore p del test risulta essere estremamente basso.

Poiché questo valore è inferiore a 0,05, abbiamo prove sufficienti per affermare che i dati del campione non provengono da una popolazione distribuita normalmente.

Questo risultato non dovrebbe sorprendere poiché abbiamo generato i dati campione utilizzando la funzione rpois() , che genera valori casuali da una distribuzione di Poisson.

Correlati: una guida a dpois, ppois, qpois e rpois in R

Possiamo anche produrre un istogramma per vedere visivamente che i dati del campione non sono distribuiti normalmente:

 hist(data, col=' coral2 ') 

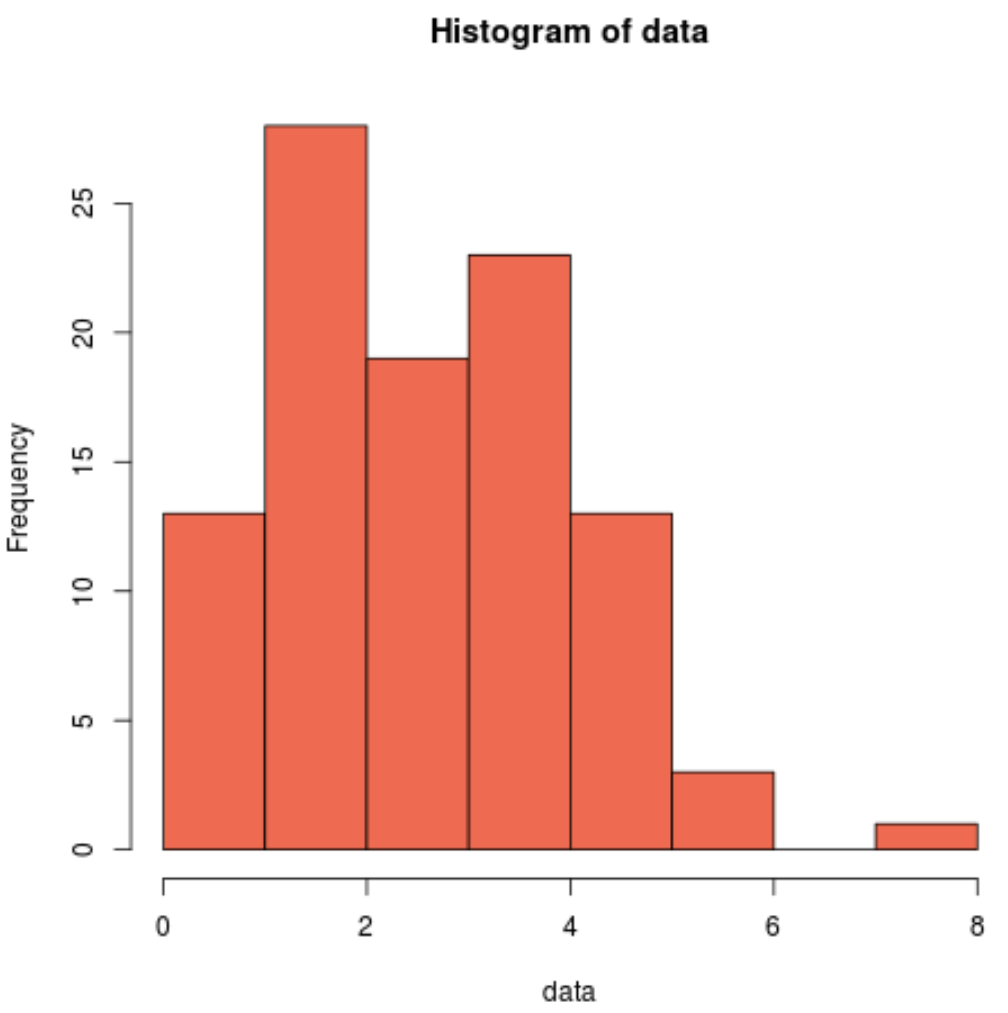
Possiamo vedere che la distribuzione è distorta a destra e non ha la tipica “forma a campana” associata ad una distribuzione normale.

Pertanto, il nostro istogramma corrisponde ai risultati del test di Cramer-Von Mises e conferma che i dati del nostro campione non provengono da una distribuzione normale.

Cosa fare con i dati non normali

Se un dato set di dati non è distribuito normalmente, spesso possiamo eseguire una delle seguenti trasformazioni per renderlo più normale:

1. Trasformazione del log: trasforma la variabile di risposta da y a log(y) .

2. Trasformazione della radice quadrata: trasforma la variabile di risposta da y a √y .

3. Trasformazione della radice del cubo: trasforma la variabile di risposta da y a y ^1/3 .

Eseguendo queste trasformazioni, la variabile di risposta generalmente si avvicina alla distribuzione normale.

Fare riferimento a questo tutorial per vedere come eseguire queste trasformazioni nella pratica.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altri test di normalità in R:

Come eseguire un test di Shapiro-Wilk in R
Come eseguire un test di Anderson-Darling in R
Come eseguire un test di Kolmogorov-Smirnov in R