Come calcolare asimmetria e curtosi in sas

In statistica, l’asimmetria e la curtosi sono due modi per misurare la forma di una distribuzione.

L’asimmetria misura l’asimmetria di una distribuzione.

• Un’asimmetria negativa indica che la coda si trova sul lato sinistro della distribuzione.
• Un’inclinazione positiva indica che la coda si trova sul lato destro della distribuzione.
• Un valore pari a zero indica che non c’è asimmetria nella distribuzione, il che significa che la distribuzione è perfettamente simmetrica.

La curtosi misura se una distribuzione è pesante o leggera rispetto a una distribuzione normale .

• La curtosi di una distribuzione normale è 0.
• Se una data distribuzione ha una curtosi inferiore a 0, si dice che sia playkurtica , nel senso che tende a produrre meno valori anomali e meno estremi rispetto alla distribuzione normale.
• Se una data distribuzione ha una curtosi maggiore di 0, si dice che sia leptokurtica , nel senso che tende a produrre più valori anomali rispetto alla distribuzione normale.

Per calcolare l’asimmetria e la curtosi delle variabili in SAS, è possibile utilizzare le istruzioni SKEWNESS e KURTOSIS in PROC MEANS .

L’esempio seguente mostra come utilizzare queste istruzioni nella pratica.

Esempio: calcolo dell’asimmetria e della curtosi in SAS

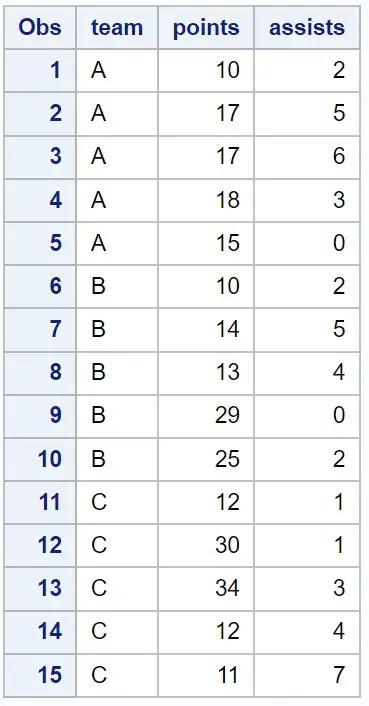
Supponiamo di avere il seguente set di dati in SAS che contiene informazioni su vari giocatori di basket:

 /*create dataset*/
data my_data;
    input team $points assists;
    datalines ;
At 10 2
At 17 5
At 17 6
At 18 3
At 15 0
B 10 2
B 14 5
B 13 4
B 29 0
B 25 2
C 12 1
C 30 1
C 34 3
C 12 4
C 11 7
;
run ;

/*view dataset*/
proc print data =my_data; 

Possiamo utilizzare PROC MEANS con le istruzioni SKEWNESS e KURTOSIS per calcolare l’asimmetria e la curtosi di ciascuna variabile numerica nel set di dati:

 /*calculate skewness and kurtosis for each numeric variable*/
proc means data =my_data SKEWNESS KURTOSIS ;
run ; 

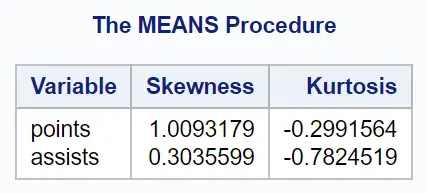
La tabella di output mostra i valori di asimmetria e curtosi per ciascuna variabile numerica nel set di dati:

(1) punti

• La variabile punti ha un’asimmetria di 1.009 . Poiché questo valore è maggiore di 0, significa che la coda si trova sul lato destro della distribuzione.
• La variabile punti ha una curtosi di -0.299 . Poiché questo valore è inferiore a 0, significa che la distribuzione ha leggermente meno valori anomali e valori meno estremi rispetto alla distribuzione normale.

(2) aiuto

• La variabile assist ha un’asimmetria di 0,304 . Poiché questo valore è maggiore di 0, significa che la coda si trova sul lato destro della distribuzione.
• La variabile di supporto ha una curtosi di -0.782 . Poiché questo valore è inferiore a 0, significa che la distribuzione presenta meno valori anomali e valori estremi rispetto alla distribuzione normale.

Per visualizzare la distribuzione dei valori per ciascuna variabile numerica nel set di dati, è possibile utilizzare PROC UNIVARIATE per creare istogrammi per le variabili punto e assistite:

 /*create histograms for points and assists variables*/
proc univariate data =my_data;
    var points assists;
    histogram points assists;
run ;

Ciò produce il seguente istogramma per la variabile points :

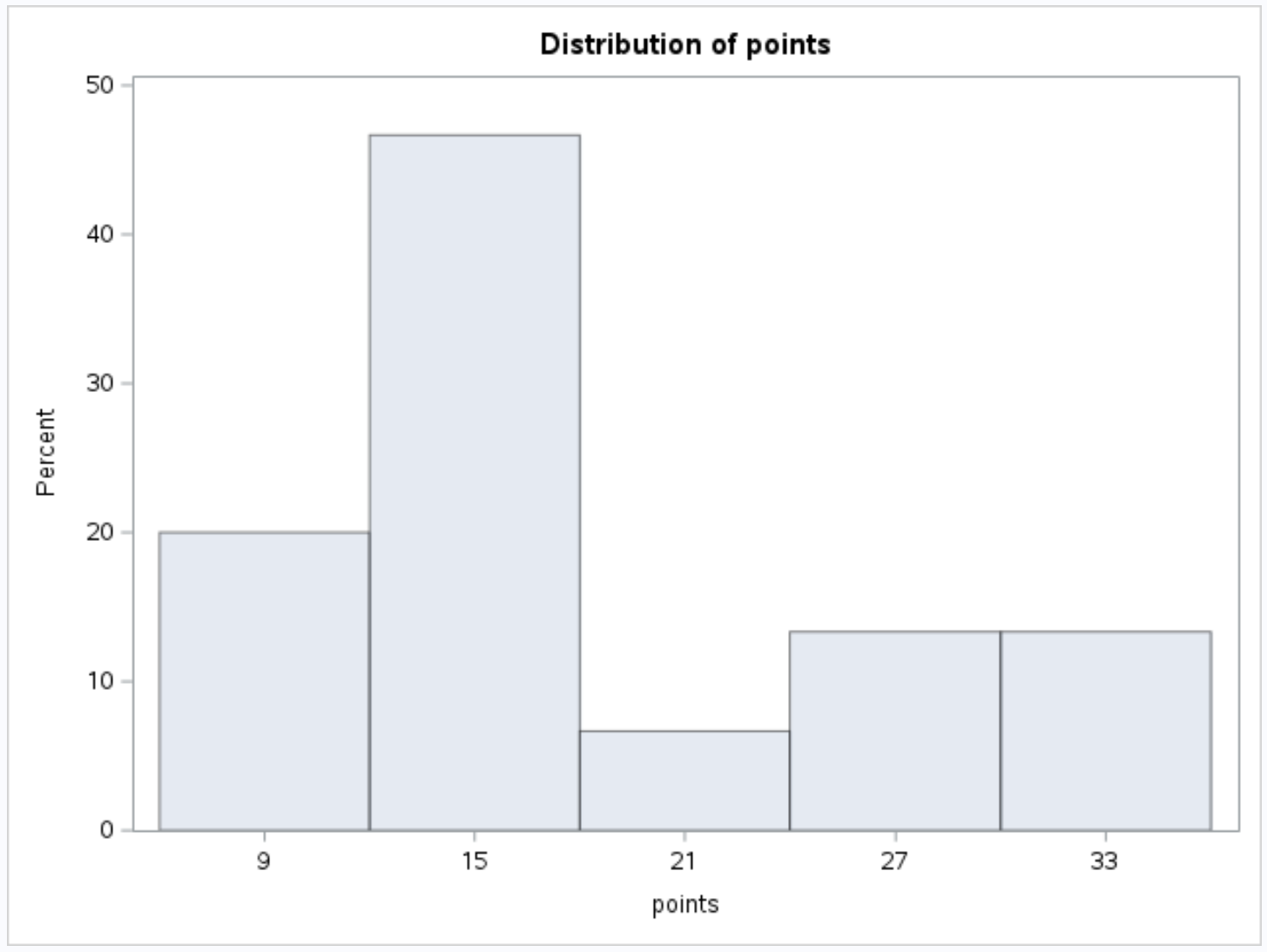
E il seguente istogramma per la variabile di assistenza :

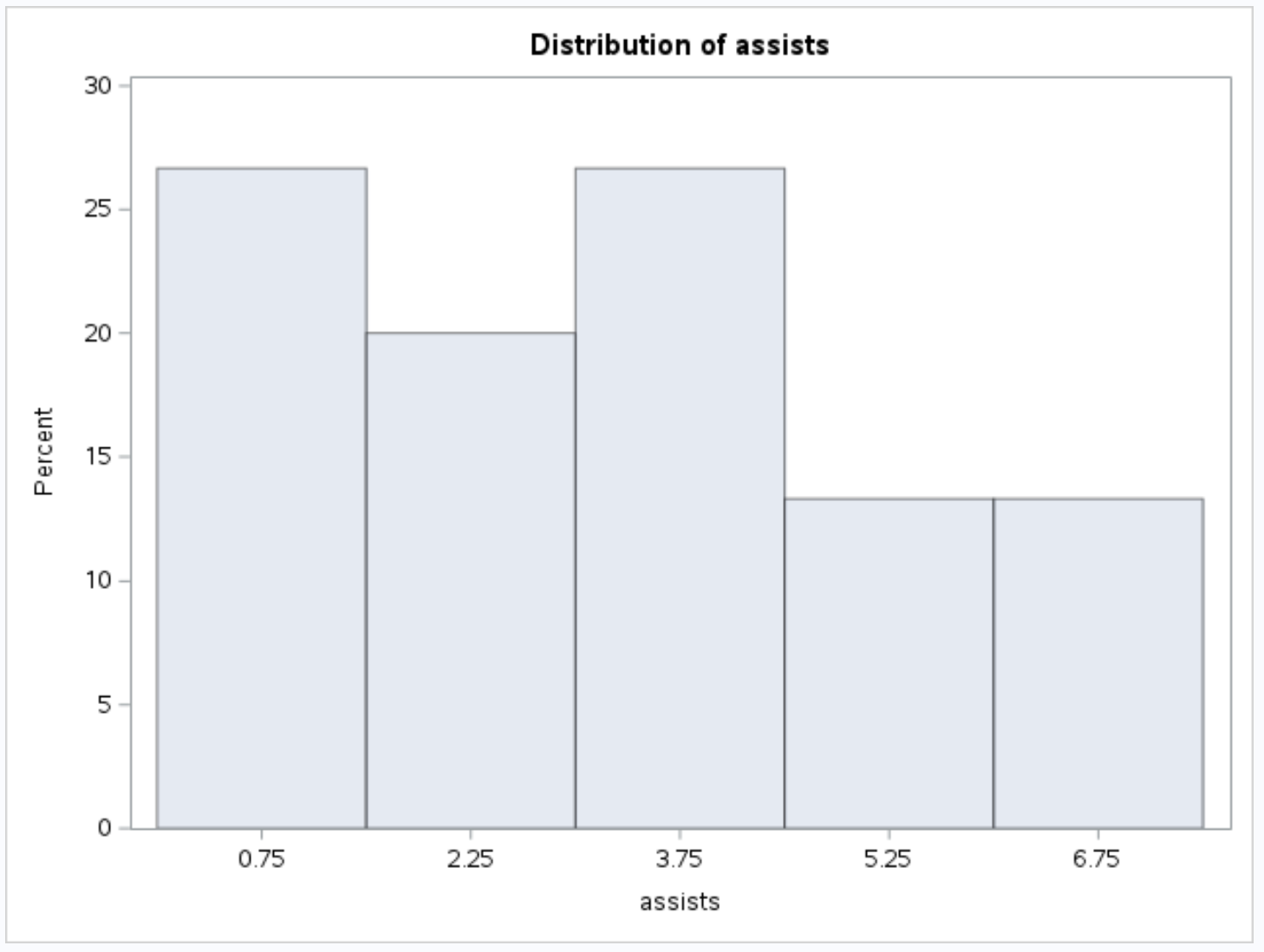
Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SAS:

Come calcolare le statistiche descrittive in SAS
Come creare tabelle di frequenza in SAS
Come calcolare i percentili in SAS
Come creare tabelle pivot in SAS