Come calcolare asimmetria e curtosi in r

In statistica, l’asimmetria e la curtosi sono due modi per misurare la forma di una distribuzione.

L’asimmetria è una misura dell’asimmetria di una distribuzione. Questo valore può essere positivo o negativo.

• Un’asimmetria negativa indica che la coda si trova sul lato sinistro della distribuzione, che si estende verso valori più negativi.
• Un’inclinazione positiva indica che la coda si trova sul lato destro della distribuzione, che si estende verso valori più positivi.
• Un valore pari a zero indica che non c’è asimmetria nella distribuzione, il che significa che la distribuzione è perfettamente simmetrica.

La curtosi misura se una distribuzione è pesante o leggera rispetto a una distribuzione normale .

• La curtosi di una distribuzione normale è 3.
• Se una data distribuzione ha una curtosi inferiore a 3, si dice che sia playkurtica , nel senso che tende a produrre meno valori anomali e meno estremi rispetto alla distribuzione normale.
• Se una data distribuzione ha una curtosi maggiore di 3, si dice che sia leptokurtica , nel senso che tende a produrre più valori anomali rispetto alla distribuzione normale.

Nota: alcune formule (definizione di Fisher) sottraggono 3 dalla curtosi per facilitare il confronto con la distribuzione normale. Utilizzando questa definizione, una distribuzione avrebbe una curtosi maggiore di una distribuzione normale se avesse un valore di curtosi maggiore di 0.

Questo tutorial spiega come calcolare sia l’asimmetria che la curtosi di un dato set di dati in R.

Esempio: Asimmetria e appiattimento in R

Supponiamo di avere il seguente set di dati:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Possiamo visualizzare rapidamente la distribuzione dei valori in questo set di dati creando un istogramma:

 hist(data, col=' steelblue ') 

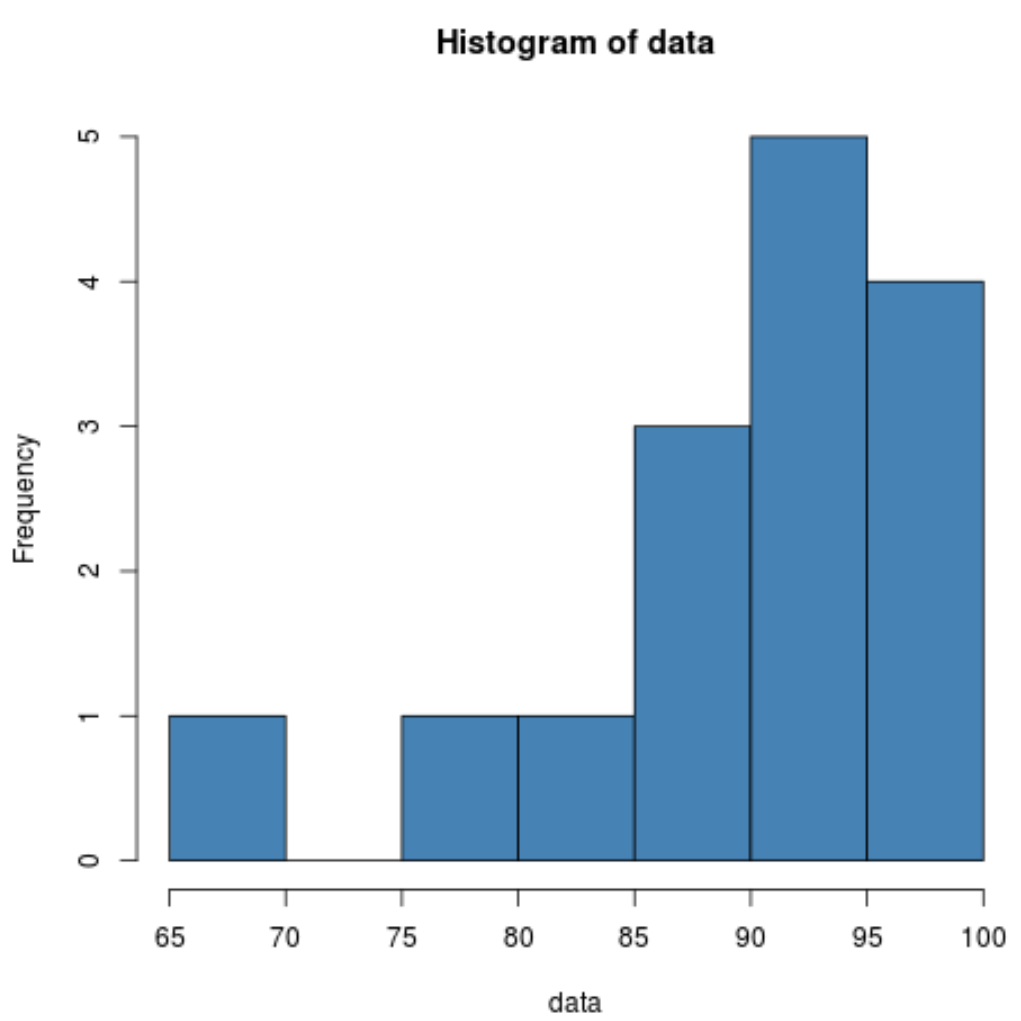
L’istogramma ci mostra che la distribuzione sembra essere sbilanciata a sinistra. Cioè, una porzione maggiore dei valori si concentra sul lato destro della distribuzione.

Per calcolare l’asimmetria e la curtosi di questo set di dati, possiamo utilizzare le funzioni skewness() e kurtosis() dalla libreria moment in R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

L’asimmetria risulta essere -1.391777 e la curtosi risulta essere 4.177865 .

Poiché l’asimmetria è negativa, ciò indica che la distribuzione è lasciata asimmetrica. Ciò conferma quanto visto nell’istogramma.

Poiché la curtosi è maggiore di 3, ciò indica che la distribuzione ha più valori nelle code rispetto ad una distribuzione normale.

La libreria dei momenti offre anche la funzione jarque.test() , che esegue un test di bontà di adattamento che determina se i dati del campione presentano o meno asimmetria e curtosi coerenti con una distribuzione normale. Le ipotesi nulla e alternativa di questo test sono le seguenti:

Ipotesi nulla : il set di dati presenta asimmetria e curtosi che corrispondono a una distribuzione normale.

Ipotesi alternativa : il set di dati presenta disallineamento e curtosi che non corrispondono a una distribuzione normale.

Il codice seguente mostra come eseguire questo test:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

Il valore p del test risulta essere 0,05756 . Poiché questo valore non è inferiore a α = 0,05, non possiamo rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che questo set di dati presenta asimmetria e curtosi diverse dalla distribuzione normale.

Puoi trovare la documentazione completa della Libreria Moments qui .

Bonus: calcolatore di asimmetria e curtosi

È inoltre possibile calcolare l’asimmetria per un determinato set di dati utilizzando il calcolatore statistico di asimmetria e curtosi , che calcola automaticamente l’asimmetria e la curtosi per un determinato set di dati.