Cosa sono le curve di densità? (spiegazione ed esempi)

Una curva di densità è una curva su un grafico che rappresenta la distribuzione dei valori in un insieme di dati. Ciò è utile per tre motivi:

1. Una curva di densità ci dà una buona idea della “forma” di una distribuzione, compreso se una distribuzione ha o meno uno o più “picchi” di valori di frequenza e se la distribuzione è o meno sbilanciata verso sinistra o destra. GIUSTO. .

2. Una curva di densità ci consente di vedere visivamente dove si relazionano la media e la mediana di una distribuzione.

3. Una curva di densità ci consente di vedere visivamente quale percentuale di osservazioni in un set di dati rientra tra valori diversi.

La curva di densità più conosciuta è la curva a campana che rappresenta la distribuzione normale .

Per comprendere meglio le curve di densità, considerare il seguente esempio.

Esempio: creazione e interpretazione di una curva di densità

Supponiamo di avere il seguente set di dati che mostra l’altezza di 20 piante diverse (in pollici) in un determinato campo:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Se creassimo un semplice istogramma per visualizzare le frequenze relative di ciascun valore, sarebbe simile a questo:

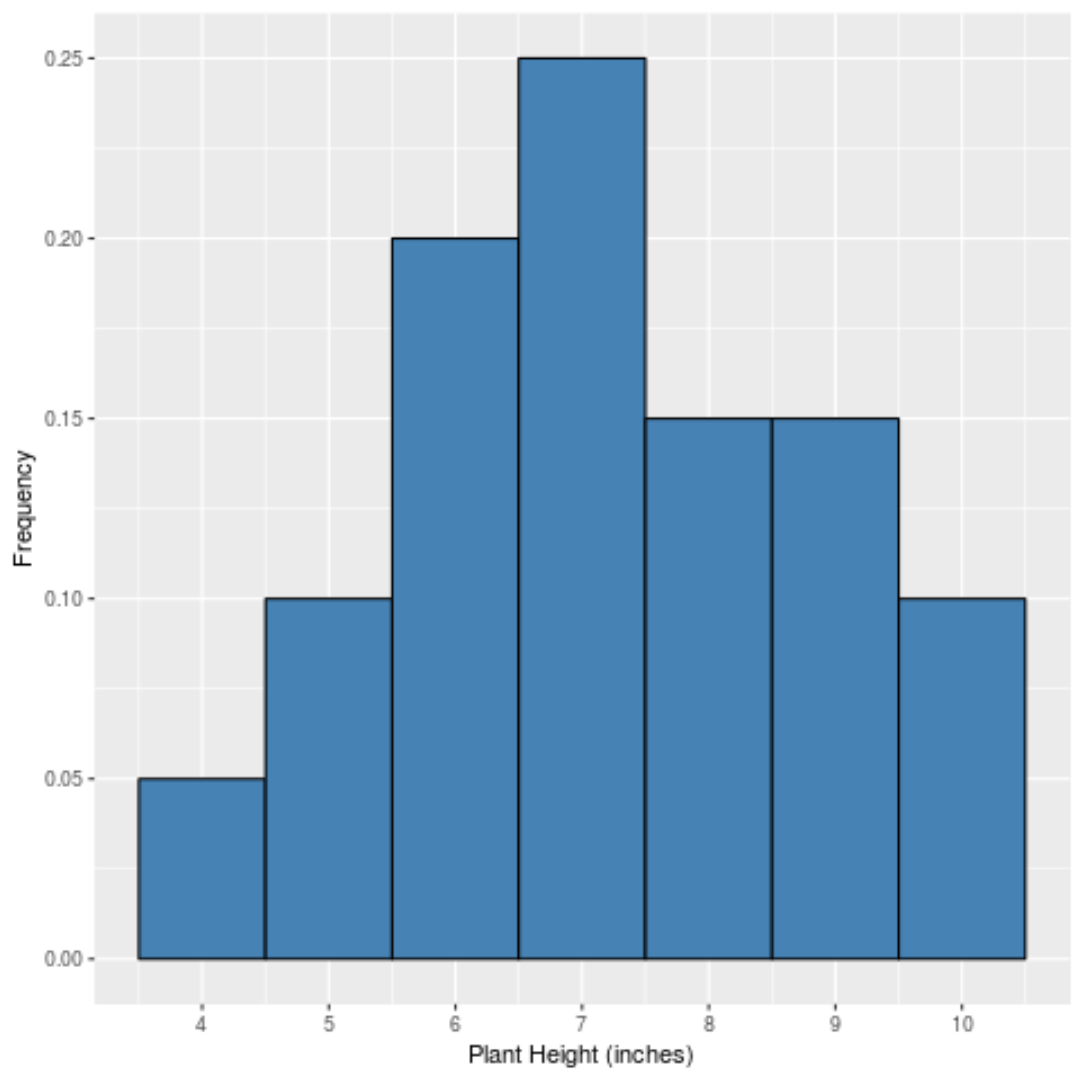
L’asse x mostra il valore dei dati e l’asse y mostra la frequenza relativa (ad esempio, il valore “7” appare 5 volte su 20 valori totali nel set di dati, quindi ha una frequenza relativa del 25% o 0,25 .

E se creassimo una curva di densità per catturare la “forma” di questa distribuzione, sarebbe simile a questa:

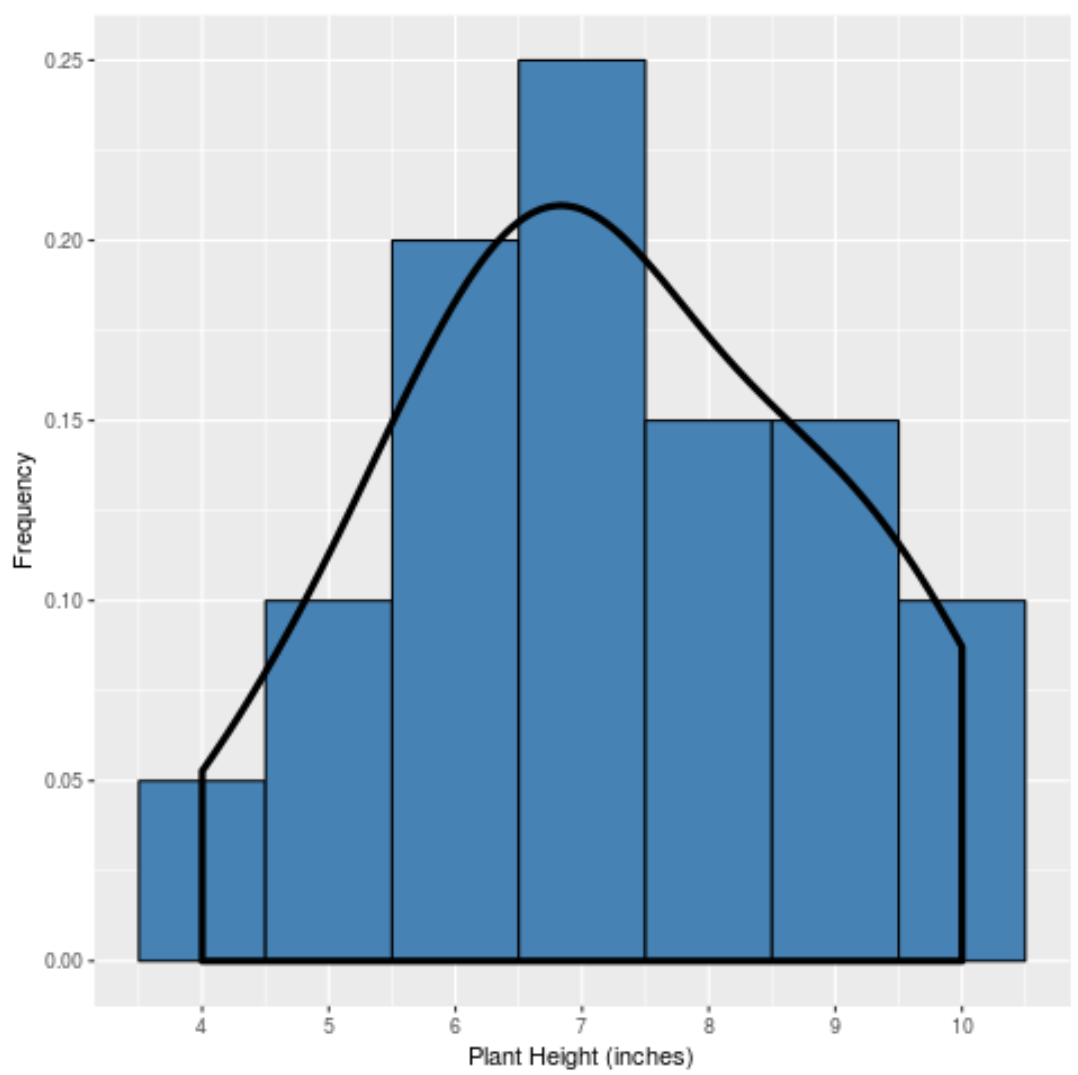
La curva è più alta vicino al centro della distribuzione perché è lì che si trovano la maggior parte dei valori. È anche più basso vicino alle estremità della distribuzione perché meno piante assumono questi valori (ad esempio altezza 4 pollici o 10 pollici).

Come interpretare le curve di densità

Le curve di densità sono disponibili in tutte le forme e dimensioni e ci consentono di ottenere una rapida comprensione visiva della distribuzione dei valori in un dato set di dati. Sono particolarmente utili per aiutarci a visualizzare:

1. Asimmetria

L’asimmetria è un modo per descrivere la simmetria di una distribuzione. Le curve di densità ci consentono di vedere rapidamente se un grafico è inclinato a sinistra, a destra o non ha inclinazione:

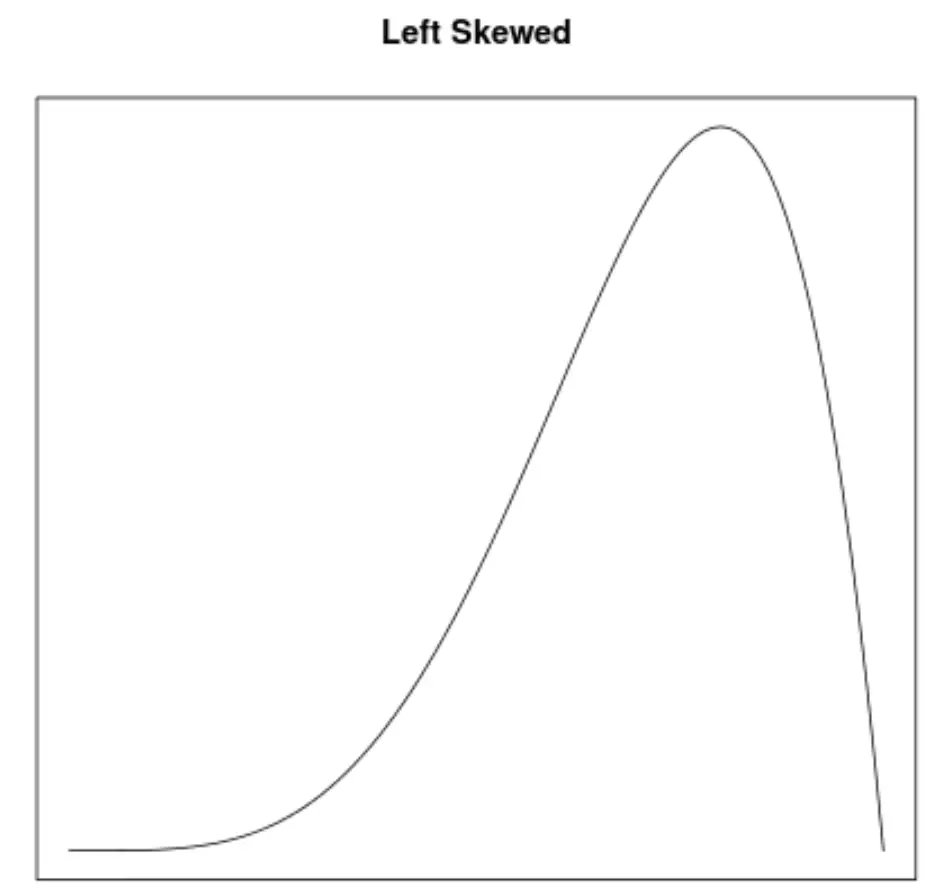
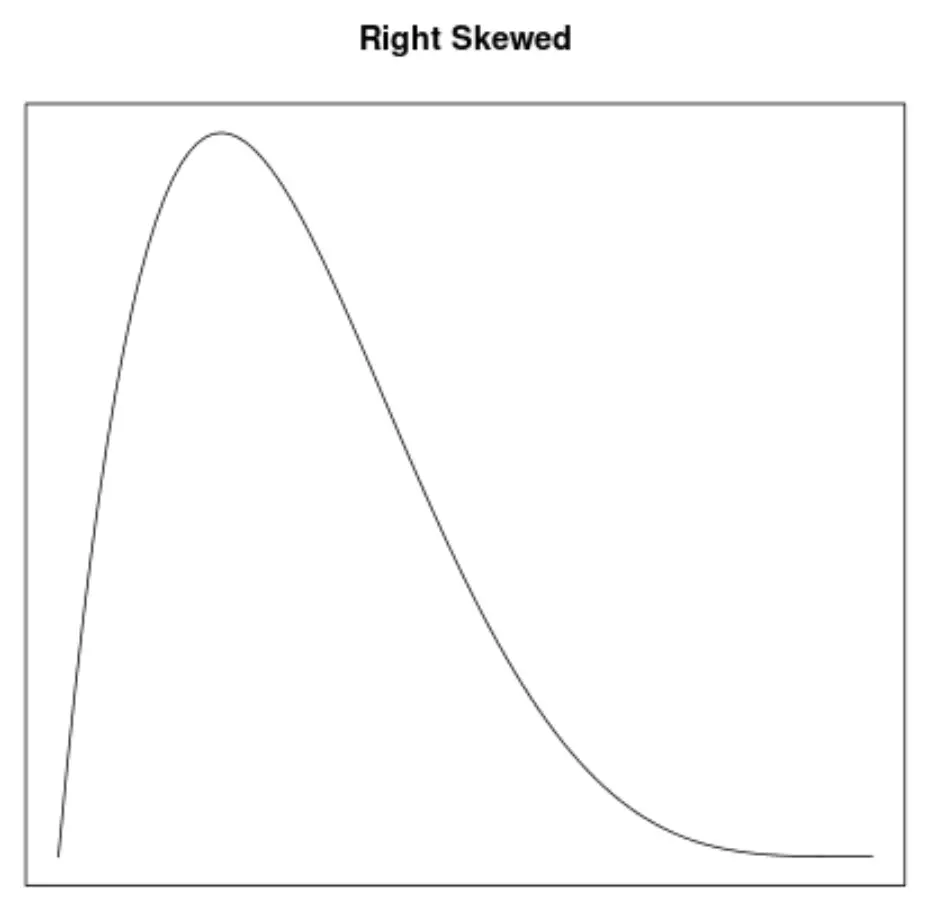
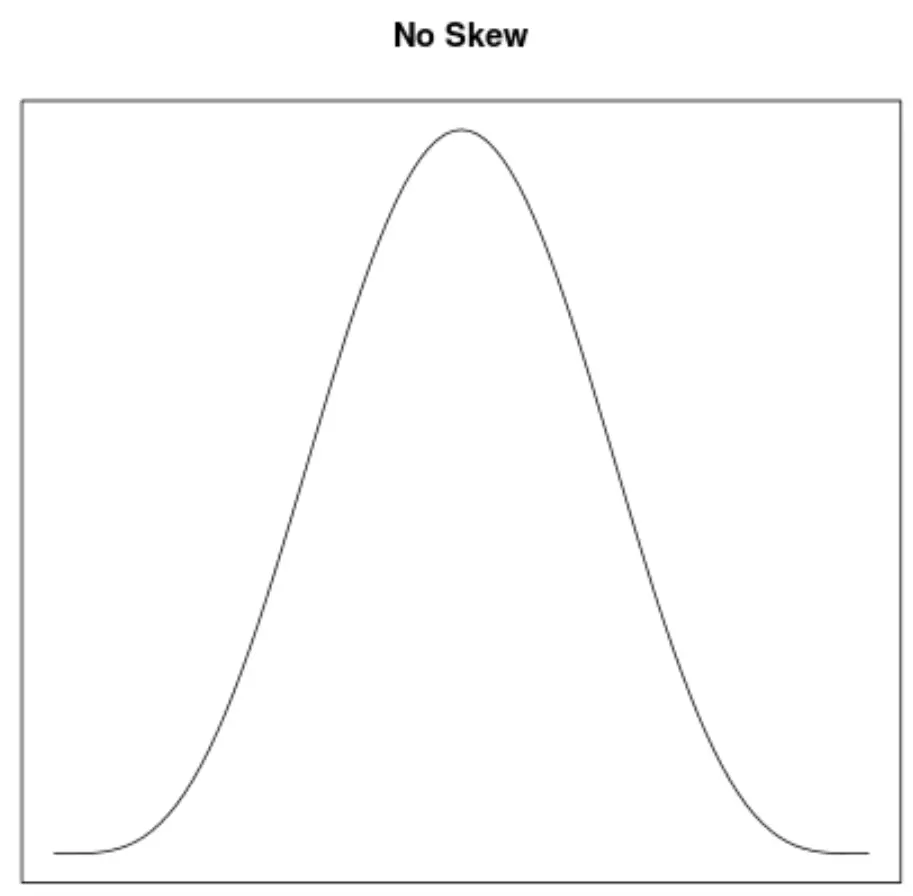
2. La posizione della media e della mediana

In base all’asimmetria di una curva di densità, possiamo dire rapidamente se la media o la mediana è maggiore in una data distribuzione. Particolarmente:

• Se una curva di densità rimane asimmetrica , la media è inferiore alla mediana.
• Se una curva di densità è inclinata a destra , la media è maggiore della mediana.
• Se una curva di densità non ha asimmetria , allora la media è uguale alla mediana.

3. Numero di picchi

Le curve di densità ci permettono anche di vedere rapidamente quanti “picchi” ci sono in una data distribuzione. In ciascuno degli esempi precedenti, le distribuzioni avevano un solo picco, quindi descriveremmo queste distribuzioni come unimodali .

Tuttavia, alcune distribuzioni possono avere due picchi che chiamiamo distribuzioni bimodali . E in rari casi possiamo avere anche distribuzioni multimodali con due o più picchi.

Creando semplicemente una curva di densità per un dato set di dati, possiamo vedere rapidamente quanti picchi sono presenti nella distribuzione.

Proprietà delle curve di densità

Le curve di densità hanno le seguenti proprietà:

• La somma dell’area sotto la curva corrisponde sempre al 100%.
• La curva non andrà mai sotto l’asse x.

Tieni a mente questi due fatti quando crei o interpreti le curve di densità per diverse distribuzioni.

Risorse addizionali

Introduzione agli istogrammi di frequenza relativi
Come creare una curva a campana in Excel
Come creare una curva a campana in Python