Decili

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

In questo articolo spieghiamo cosa sono i decili e come si calcolano. Troverai anche diversi esempi risolti passo passo di calcolo dei decili e, inoltre, potrai calcolare i decili di qualsiasi campione statistico con un calcolatore online.

Cosa sono i decili?

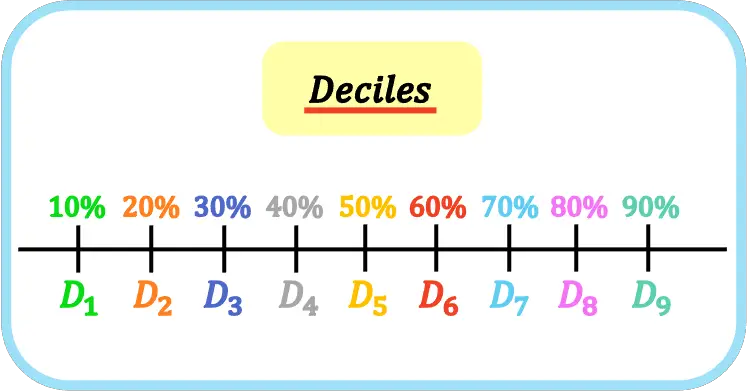
In statistica i decili sono i nove valori che dividono un insieme di dati ordinati in dieci parti uguali. In modo che il primo, il secondo, il terzo,… decile rappresentino il 10%, 20%, 30%,… del campione o della popolazione.

Ad esempio, il valore del quarto decile è superiore al 40% dei dati, ma inferiore al resto dei dati.

I decili sono rappresentati dalla lettera maiuscola D e dall’indice del decile, ovvero il primo decile è D ₁ , il secondo decile è D ₂ , il terzo decile è D ₃ , ecc.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare i decili per qualsiasi set di dati.

Va notato che i decili sono una misura della posizione non centrale allo stesso modo dei quartili, dei quintili e dei percentili. Puoi verificare il significato di ciascuno di questi tipi di quantili sul nostro sito web.

Inoltre, il quinto decile è equivalente alla mediana e al secondo quartile, poiché dividono l’intero set di dati in due parti uguali.

Come calcolare i decili

Per calcolare la posizione decile di una serie di dati statistici, moltiplicare il numero decile per la somma del numero totale di dati più uno e dividere il risultato per dieci.

La formula del decile è quindi:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Nota: questa formula ci dice la posizione del decile, non il valore del decile. Il decile sarà il dato situato nella posizione ottenuta dalla formula.

Tuttavia, a volte il risultato di questa formula ci darà un numero decimale, dobbiamo quindi distinguere due casi a seconda che il risultato sia un numero decimale o meno:

Se il risultato della formula è un numero senza parte decimale , il decile è il dato situato nella posizione prevista dalla formula sopra.
Se il risultato della formula è un numero con parte decimale , il valore decile viene calcolato utilizzando la seguente formula:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Dove x _i e x _i+1 sono i numeri delle posizioni tra le quali si trova il numero ottenuto dalla prima formula, e d è la parte decimale del numero ottenuto dalla prima formula.

Ora potresti pensare che ottenere i decili di un campione statistico sia complesso, ma in pratica è abbastanza semplice. Se leggi i due esempi seguenti, sicuramente lo capirai molto meglio.

Nota : la comunità scientifica non è del tutto d’accordo su come calcolare i decili, quindi puoi trovare libri di statistica che lo spiegano in modo leggermente diverso.

Esempio di calcolo del decile

Come hai visto sopra, il calcolo dei decili dipende dal fatto che il numero che ci fornisce la prima formula sia decimale o meno, ecco perché di seguito abbiamo preparato due esempi risolti, uno per ogni caso. In ogni caso, ricorda che se hai domande sulla composizione dei decili, puoi farle nei commenti.

Esempio 1

Dati i seguenti dati, dal più piccolo al più grande, trova il primo, il terzo e l’ottavo decile del campione.

I dati in questo esercizio sono già ordinati, quindi non è necessario modificare l’ordine, altrimenti dovremmo prima ordinare i dati dal più piccolo al più grande.

Come spiegato in precedenza, la formula che permette di trovare le posizioni dei decili è la seguente:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

La dimensione del campione per questo esercizio è di 29 osservazioni, quindi per calcolare la posizione del primo decile devi sostituire 29 per n e 1 per k :

$\cfrac{1\cdot (29+1)}{10}=3\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_1=85$

Il risultato della formula è 3, quindi il primo decile sarà nella terza posizione dell’elenco ordinato e questo valore corrisponde a 85.

Ora applichiamo nuovamente la stessa procedura ma con il terzo decile. Usiamo la formula sostituendo la k con un 3:

$\cfrac{3\cdot (29+1)}{10}=9\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_3=97$

Il terzo decile sarà quindi l’elemento in nona posizione, cioè 97.

Infine, eseguiamo lo stesso procedimento ma inseriamo 8 nella formula per determinare l’ottavo decile:

$\cfrac{8\cdot (29+1)}{10}=24\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_8=131$

L’ottavo decile sarà il numero nella posizione 24 dell’elenco di dati ordinato, quindi l’ottavo decile è 131.

Esempio 2

Dai dati nella tabella seguente, calcola i decili 4, 7 e 9.

Come nell’esempio precedente, per ottenere le posizioni dei decili è necessario utilizzare la seguente formula:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

In questo caso la dimensione del campione è 42, quindi per trovare la posizione del quarto decile è necessario sostituire il parametro n con 42 e il k con 4:

$\cfrac{4\cdot (42+1)}{10}=17,2$

Ma questa volta abbiamo ottenuto un numero decimale dalla formula, quindi dobbiamo applicare la seguente formula per calcolare il decile esatto:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Il numero ottenuto dalla prima formula è 17,2, quindi il quarto decile è compreso tra il diciassettesimo e il diciottesimo indicati, che sono rispettivamente 109 e 112. Pertanto x _i è 109, x _{i+ 1} è 112 e d è la parte decimale. del numero ottenuto, cioè 0,2.

$D_4=109+0,2\cdot (112-109)=109,6$

Ripetiamo lo stesso procedimento per trovare il settimo decile. Per prima cosa calcoliamo la posizione del decile:

$\cfrac{7\cdot (42+1)}{10}=30,1$

Dalla formula abbiamo ottenuto il numero 30.1, il che significa che il decile sarà compreso tra le posizioni 30 e 31, i cui valori sono 154 e 159. Il calcolo del decile esatto è quindi:

$D_7=154+0,1\cdot (159-154)=154,5$

Infine applichiamo nuovamente lo stesso metodo per ottenere il nono decile. Determiniamo la posizione del decile:

$\cfrac{9\cdot (42+1)}{10}=38,7$

Il numero ottenuto è decimale ed è compreso tra 38 e 39, le cui posizioni corrispondono ai valori 189 e 196. Pertanto il calcolo del decile 9 è:

$D_9=189+0,7\cdot (196-189)=193,9$

Calcolatore dei decili

Inserisci un set di dati statistici nella calcolatrice qui sotto per calcolare i decili. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Decili nei dati raggruppati

Per calcolare i decili quando i dati vengono raggruppati in intervalli , dobbiamo prima trovare l’intervallo o il contenitore in cui rientra il decile utilizzando la seguente formula:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,3,4,5,6,7,8,9$

Il decile si troverà quindi nell’intervallo la cui frequenza assoluta è immediatamente maggiore del numero ottenuto nell’espressione precedente.

E una volta che conosciamo già l’intervallo a cui appartiene il decile, dobbiamo applicare la seguente formula per trovare il valore esatto del decile:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4,5,6,7,8,9$

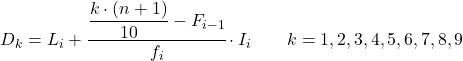
Oro:

L _i è il limite inferiore dell’intervallo in cui si trova il decile.
n è il numero totale di dati statistici.
F _i-1 è la frequenza assoluta cumulativa dell’intervallo precedente.
f _i è la frequenza assoluta dell’intervallo in cui si trova il decile.
I _i è la larghezza dell’intervallo decile.

Per farti vedere come si fa, di seguito hai un esercizio completato in cui vengono calcolati i decili 3, 5 e 8 dei seguenti dati raggruppati per intervalli.

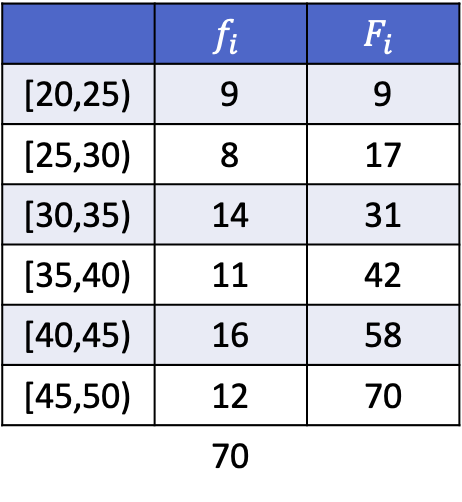
Poiché i dati sono raggruppati, il calcolo di ciascun decile consiste in due passaggi: innanzitutto, trovare l’intervallo in cui cade il decile, quindi calcolare il valore esatto del decile. Troviamo quindi l’intervallo del terzo decile:

$\cfrac{k\cdot (n+1)}{10}$

$\cfrac{3\cdot (70+1)}{10} =21,3 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [30,35)$

L’intervallo decile sarà quello la cui frequenza cumulativa assoluta è immediatamente maggiore di 21,3, e in questo caso è l’intervallo [30,35) la cui frequenza cumulativa assoluta è 31. Ora che conosciamo l’intervallo decile, applichiamo la seguente formula per trovare il valore esatto del decile:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i$

$D_3=30+ \cfrac{\displaystyle\frac{3\cdot (70+1)}{10}-17}{14}\cdot 5=31,54$

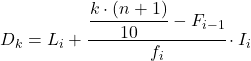
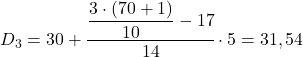
Dobbiamo ora riapplicare il metodo per ottenere il quinto decile. Per prima cosa determiniamo l’intervallo in cui si trova:

$\cfrac{5\cdot (70+1)}{10} =35,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [35,40)$

Il risultato 35 significa che è nell’intervallo [35,40) ma non perché c’è un 35 nell’espressione dell’intervallo, ma perché la sua frequenza assoluta accumulata (42) è la più immediatamente alta. E una volta individuato l’intervallo, applichiamo la seconda formula del processo:

$D_5=35+ \cfrac{\displaystyle\frac{5\cdot (70+1)}{10}-31}{11}\cdot 5=37,05$

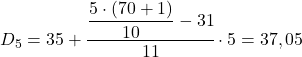
Infine troviamo l’ottavo decile. Per fare ciò, calcoliamo prima il suo intervallo:

$\cfrac{8\cdot (70+1)}{10} =56,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [40,45)$

La frequenza assoluta cumulativa immediatamente superiore a 56,8 è 58, quindi l’intervallo dell’ottavo decile è [40,45). È quindi sufficiente determinare il valore esatto del decile:

$D_8=40+ \cfrac{\displaystyle\frac{8\cdot (70+1)}{10}-42}{16}\cdot 5=44,63$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più