Deviazione quasi standard

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la deviazione quasi standard nelle statistiche e come viene calcolata. Troverai quindi la formula della deviazione quasi standard, un esercizio risolto e, inoltre, un calcolatore online per calcolare la deviazione quasi standard di qualsiasi set di dati.

Cos’è la deviazione quasi standard?

In statistica, la deviazione quasi standard è una misura di dispersione che indica la variabilità del campione. Nello specifico, la deviazione quasi standard è uguale alla radice quadrata della somma dei quadrati delle deviazioni divisa per il numero totale di punti dati meno uno.

Il simbolo della deviazione quasi standard è σ _n-1 os _n-1 .

La deviazione quasi standard può anche essere chiamata deviazione quasi standard e talvolta è anche chiamata deviazione standard del campione, perché di solito viene calcolata utilizzando i valori di un campione statistico. Di seguito entreremo nei dettagli sulla differenza tra deviazione quasi standard e deviazione standard.

Formula della deviazione quasi standard

La deviazione quasi standard è uguale alla radice quadrata della somma dei quadrati delle deviazioni della serie di dati divisa per il numero totale di osservazioni meno uno. Pertanto, la formula per calcolare la deviazione quasi standard è:

Oro:

$\sigma_{n-1}$

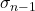
Questa è la deviazione quasi standard.
$x_i$

è il valore dei dati

$i$

.
$n$

è il numero totale di dati.
$\overline{x}$

è la media del set di dati.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la deviazione quasi standard per qualsiasi set di dati.

Esempio di calcolo della deviazione quasi standard

Considerando la definizione di deviazione quasi standard, di seguito puoi vedere un semplice esempio di come calcolare la deviazione quasi standard di un set di dati.

Il budget di un’azienda per il reparto di ricerca e sviluppo è molto volatile, perché dipende dal profitto economico che l’azienda ha ottenuto nell’anno precedente. Pertanto, il budget per questa sezione negli ultimi cinque anni è stato: 3, 6, 2, 9, 4 milioni di euro. Calcola la deviazione quasi standard di questa serie di dati.

La prima cosa che dobbiamo fare per determinare la deviazione quasi standard è calcolare la media aritmetica del campione. Per fare ciò, sommiamo tutti i dati e li dividiamo per il numero totale di osservazioni, che è cinque:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Successivamente, applichiamo la formula della deviazione quasi standard:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

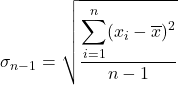
Sostituiamo i dati nella formula:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

E infine calcoliamo la deviazione quasi standard:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

In breve, la deviazione quasi standard del campione di dati è 2,77 milioni.

➤ Vedi: Quasivarianza

Calcolatore della deviazione quasi standard

Inserisci un set di dati statistici nel calcolatore online di seguito per calcolare la sua deviazione quasi standard. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Deviazione quasi standard e deviazione standard

Infine, vedremo qual è la differenza tra deviazione quasi standard e deviazione standard, poiché sono due misure statistiche diverse che hanno un nome molto simile e vengono calcolate in modo molto simile.

La differenza tra la deviazione quasi standard e la deviazione standard è il denominatore della formula. Per calcolare la deviazione quasi standard, dividere per n-1, ma la deviazione standard si calcola dividendo per n.

Pertanto, la deviazione quasi standard e la deviazione standard sono matematicamente correlate, poiché la deviazione quasi standard è equivalente alla deviazione standard moltiplicata per la radice quadrata di n (numero totale di punti dati) su n-1.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

Dall’equazione precedente possiamo dedurre che, per lo stesso insieme di dati, il valore della deviazione quasi standard sarà sempre maggiore del valore della deviazione standard.

Inoltre, la formula della deviazione quasi standard viene spesso utilizzata per calcolare la deviazione standard di un campione perché elimina le distorsioni. La deviazione quasi standard è quindi un buon stimatore della deviazione standard della popolazione. Questo è il motivo per cui, quando si fa un’inferenza statistica da un campione, è abbastanza comune dire che viene calcolata la deviazione standard quando in realtà viene calcolata la deviazione quasi standard.

➤ Vedi: Proprietà della deviazione standard

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più