Deviazione standard del campione (o deviazione standard del campione)

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la deviazione standard campionaria nelle statistiche. Allo stesso modo, imparerai come calcolare la deviazione standard del campione, un esercizio risolto e qual è la differenza tra la deviazione standard del campione e la deviazione standard della popolazione. Infine, puoi calcolare qualsiasi deviazione standard del campione con un calcolatore online.

Qual è la deviazione standard del campione?

La deviazione standard campionaria (o deviazione standard campionaria ) è una misura di dispersione che indica la variabilità di un campione. Più precisamente, la deviazione standard del campione è uguale alla radice quadrata della somma dei quadrati delle deviazioni divisa per la dimensione del campione meno uno.

Il simbolo della deviazione standard del campione è la lettera minuscola s .

La deviazione standard del campione è talvolta chiamata deviazione quasi standard (o deviazione quasi standard) per distinguerla dalla deviazione standard della popolazione. Di seguito vedremo come la deviazione standard del campione differisce dalla deviazione standard della popolazione.

Esempio di formula di deviazione standard

La deviazione standard del campione è uguale alla radice quadrata della somma dei quadrati delle deviazioni dei dati del campione divisa per la dimensione del campione meno uno. Pertanto, la formula per calcolare la deviazione standard del campione è:

formula per la deviazione standard del campione o la deviazione standard del campione.png

Oro:

$s$

è la deviazione standard del campione (o deviazione standard del campione).
$x_i$

è il valore dei dati

$i$

.
$n$

è la dimensione del campione
$\overline{x}$

è la media del campione.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la deviazione standard di qualsiasi campione di dati.

Esempio di calcolo della deviazione standard del campione

Ora che conosciamo la definizione di deviazione standard campionaria (o deviazione standard campionaria) e qual è la sua formula, risolveremo un semplice esempio per finire di capire come viene calcolata.

Un’azienda calzaturiera sta conducendo una ricerca di mercato per decidere se lanciare un nuovo modello di scarpe. Dato che esistono molti modelli diversi e vuoi solo fare una rapida analisi preliminare, decidi di guardare solo il prezzo di un campione dei cinque principali marchi di scarpe concorrenti (i prezzi sono mostrati di seguito). Qual è la deviazione standard di questo set di dati?

€98 €70 €125 €89 €75

Per calcolare la deviazione standard del campione, dobbiamo prima calcolare la media campionaria :

$\overline{x}=\cfrac{98+70+125+89+75}{5}=91,4$

Una volta calcolata la media campionaria, applichiamo la formula della deviazione standard campionaria:

$\displaystyle s=\sqrt{\frac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n-1}}$

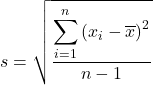
Sostituiamo i dati del campione nella formula:

$\displaystyle s=\sqrt{\frac{\displaystyle (98-91,4)^2+(70-91,4)^2+(125-91,4)^2+(89-91,4)^2+(75-91,4)^2}{5-1}}$

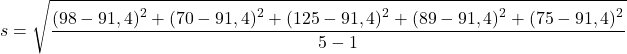
Non resta quindi che risolvere le operazioni per calcolare la deviazione standard campionaria:

$\begin{aligned}\displaystyle s&=\sqrt{\frac{6,6^2+(-21,4)^2+33,6^2+(-2,4)^2+(-16,4)^2}{4}}\\[2ex]\displaystyle s&=\sqrt{\frac{43,56+457,96+1128,96+5,76+268,96}{4}}\\[2ex]s&=\sqrt{\frac{1905,2}{4}}\\[2ex]s&=\sqrt{476,3}\\[2ex]s&=21,82 \end{aligned}$

La differenza campionaria del campione analizzato è quindi pari a €21,82.

➤ Vedi: Variazioni campionarie

Deviazione standard del campione e deviazione standard della popolazione

Successivamente, vedremo quali sono le differenze tra la deviazione standard del campione e la deviazione standard della popolazione, perché questi sono due concetti statistici correlati su cui dobbiamo essere chiari.

In estadística, la deviazione standard della popolazione è la deviazione standard che si ottiene calcolando con tutti gli elementi della popolazione, sebbene la deviazione standard sia la deviazione standard che si ottiene eseguendo il calcolo con un solo esempio di dati della popolazione .

Matematicamente, la differenza tra la deviazione standard del campione e la deviazione standard della popolazione è il denominatore della formula utilizzata per il suo calcolo. Per calcolare la deviazione standard del campione è necessario dividerla per n-1, mentre la deviazione standard della popolazione si calcola dividendo per n.

Inoltre, per differenziare la deviazione standard del campione dalla deviazione standard della popolazione, queste sono rappresentate da simboli diversi. Il simbolo della deviazione standard del campione è la lettera s, mentre il simbolo della deviazione standard della popolazione è la lettera greca σ.

In generale non tutti gli elementi di una popolazione sono noti, lo studio statistico viene quindi effettuato su un campione della popolazione. Pertanto, la deviazione standard del campione viene utilizzata per effettuare una stima puntuale del valore della deviazione standard dell’intera popolazione.

➤ Vedi: Deviazione standard della popolazione

Esempio di calcolo della deviazione standard

Inserisci i dati di un campione nel seguente calcolatore online per calcolare la sua deviazione standard del campione (o deviazione standard del campione). I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più