La relazione tra media e deviazione standard (con esempio)
La media rappresenta il valore medio in un insieme di dati.
Viene calcolato come segue:
Media campionaria = Σx i / n
Oro:
- Σ: Un simbolo che significa “somma”
- x i : l’ iesima osservazione in un set di dati
- n: il numero totale di osservazioni nel set di dati
La deviazione standard rappresenta la distribuzione dei valori in un set di dati rispetto alla media.
Viene calcolato come segue:
Deviazione standard del campione = √ Σ(x i – x bar ) 2 / (n-1)
Oro:
- Σ: Un simbolo che significa “somma”
- x i : l’i -esimo valore del campione
- x bar : Il campione significa
- n: la dimensione del campione
Nota la relazione tra la media e la deviazione standard: la media viene utilizzata nella formula per calcolare la deviazione standard .
Infatti, non possiamo calcolare la deviazione standard di un campione se non conosciamo la media campionaria.
L’esempio seguente mostra come calcolare nella pratica la media campionaria e la deviazione standard campionaria per un set di dati.
Esempio: calcolo della media e della deviazione standard per un set di dati
Supponiamo di avere il seguente set di dati che mostra i punti segnati da 10 diversi giocatori di basket:
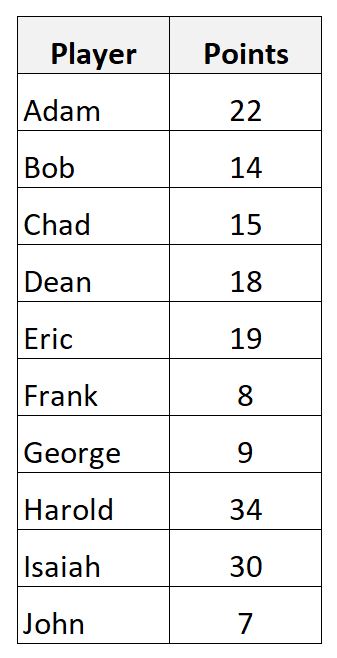Possiamo calcolare la media campionaria dei punti ottenuti utilizzando la seguente formula:
- Media campionaria = Σx i / n
- Media del campione = (22+14+15+18+19+8+9+34+30+7) / 10
- Media campionaria = 17,6
La media campionaria dei punti segnati è 17,6 . Questo rappresenta il numero medio di punti segnati tra tutti i giocatori.
Una volta che conosciamo la media campionaria, possiamo inserirla nella formula per calcolare la deviazione standard del campione:
- Deviazione standard del campione = √ Σ(x i – x bar ) 2 / (n-1)
- Deviazione standard del campione = √ ((22-17,6) 2 + (14-17,6) 2 + (15-17,6) 2 + (18-17,6) 2 + (19-17,6) 6) 2 + (8-17,6) 2 + (9 -17,6) 2 + (34-17,6) 2 + (30-17,6) 2 + (7-17,6) 2 ) / (10-1)
- Deviazione standard del campione = 9,08
La deviazione standard del campione è 9,08 . Questo rappresenta la distanza media tra ciascun valore del punto e la media del punto campione.
È utile conoscere sia la media che la deviazione standard di un set di dati perché ogni metrica ci dice qualcosa di diverso.
La media ci dà un’idea di dove si trova il valore “centrale” di un set di dati.
La deviazione standard ci dà un’idea della distribuzione dei valori attorno alla media in un insieme di dati. Quanto più alto è il valore della deviazione standard, tanto più dispersi sono i valori in un campione.
Conoscendo questi due valori, possiamo imparare molto sulla distribuzione dei valori in un set di dati.
Risorse addizionali
Le seguenti esercitazioni forniscono informazioni aggiuntive sulla media e sulla deviazione standard:
Perché la media è importante nelle statistiche?
Perché la deviazione standard è importante nelle statistiche?
Come calcolare la media e la deviazione standard in Excel
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più