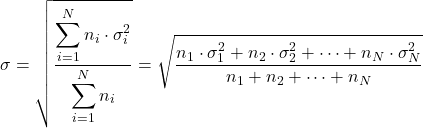Deviazione standard (o deviazione standard)

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la deviazione standard, chiamata anche deviazione standard. Imparerai come calcolare la deviazione standard, un esempio pratico passo passo e un calcolatore online per trovare la deviazione standard di qualsiasi campione di dati.

Qual è la deviazione standard (o deviazione standard)?

La deviazione standard , detta anche deviazione standard , è una misura della dispersione statistica. In altre parole, la deviazione standard è un valore che indica la dispersione di un insieme di dati statistici.

Pertanto, la deviazione standard (o deviazione standard) viene utilizzata per quantificare la dispersione di una popolazione o di un campione statistico. Maggiore è la deviazione standard di una serie di dati, maggiore è la dispersione dei dati. E l’interpretazione può essere fatta anche nella direzione opposta, se la deviazione standard è bassa significa che in generale il dato è molto vicino alla sua media.

Quando si calcola la deviazione standard o tipica su una popolazione, il simbolo della deviazione standard è la lettera greca sigma (σ). Ma quando si tratta della deviazione standard campionaria, la lettera s viene utilizzata per rappresentare la misurazione statistica.

In alcuni libri di statistica e probabilità, la deviazione standard è anche chiamata deviazione standard.

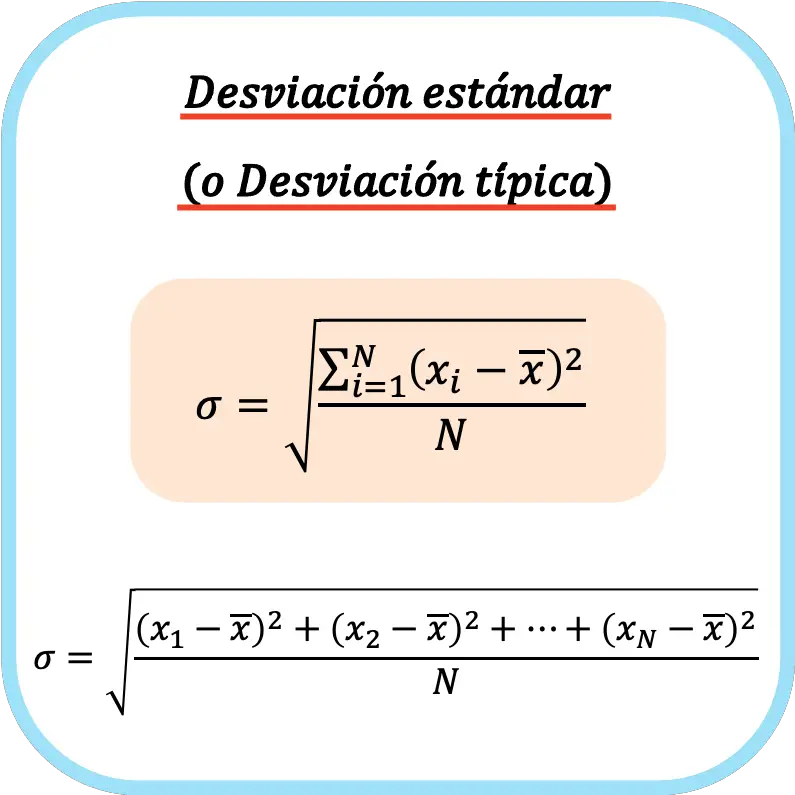
Formula della deviazione standard (o deviazione standard).

La deviazione standard (o deviazione standard) è uguale alla radice quadrata della somma dei quadrati delle deviazioni della serie di dati divisa per il numero totale di osservazioni.

La formula per calcolare la deviazione standard (o deviazione standard) è quindi:

deviazione standard, deviazione standard

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la deviazione standard di qualsiasi set di dati.

In conclusione, per trovare la deviazione standard di un set di dati, è necessario calcolare tutte le deviazioni (definite come la differenza tra un punto dati e la media aritmetica), aumentare le deviazioni a due, sommarle tutte, quindi dividere per totale. numero di dati e infine ricavare la radice quadrata.

Esempio di deviazione standard (o deviazione standard)

Considerando la definizione di deviazione standard (o deviazione tipica), di seguito è riportato un esempio passo passo in modo da poter vedere come viene calcolata la deviazione standard di una serie di dati.

Calcola la deviazione standard dei seguenti valori: 3, 6, 2, 9, 4.

La prima cosa che dobbiamo fare è determinare la media campionaria. Per fare ciò, sommiamo tutti i dati e li dividiamo per il numero totale di osservazioni, che è cinque:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Usiamo ora la formula della deviazione standard:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Sostituiamo i dati nella formula:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

E infine calcoliamo la deviazione standard:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Calcolatore della deviazione standard (o deviazione standard).

Inserisci una serie di dati statistici nel seguente calcolatore online per calcolare la sua deviazione standard (o deviazione standard). I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Deviazione standard (o tipica) per i dati raggruppati

Per calcolare la deviazione standard (o deviazione standard) dei dati raggruppati in intervalli , è necessario seguire i seguenti passaggi:

Trova la media dei dati raggruppati.
Calcolare le deviazioni dei dati raggruppati.
Quadra ogni spazio vuoto.
Moltiplicare ciascun risultato precedente per la frequenza del suo intervallo.
Aggiungi la somma di tutti i valori ottenuti nel passaggio precedente.
Dividere per il numero totale di osservazioni.
Prendi la radice quadrata del valore precedente. Il numero risultante è la deviazione standard dei dati raggruppati.

In conclusione, la formula per calcolare la deviazione standard dei dati raggruppati in intervalli è:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

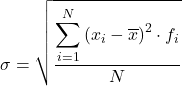
Sebbene venga normalmente utilizzata la formula precedente, è possibile utilizzare anche la seguente espressione algebrica poiché si ottiene lo stesso risultato:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

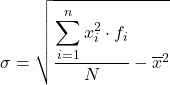
Per vedere come si fa, di seguito è riportato un esercizio passo passo sulla deviazione standard dei dati raggruppati in intervalli. Più precisamente verrà calcolata la deviazione standard dei seguenti dati statistici:

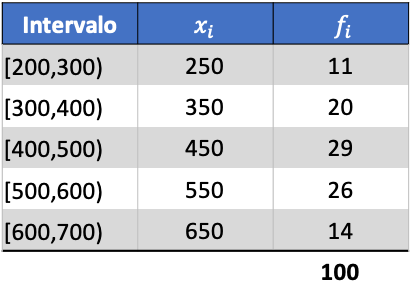
esempio di dati raggruppati in intervalli

Per prima cosa moltiplichiamo il punteggio della classe di ciascun intervallo per la sua frequenza per calcolare la media aritmetica:

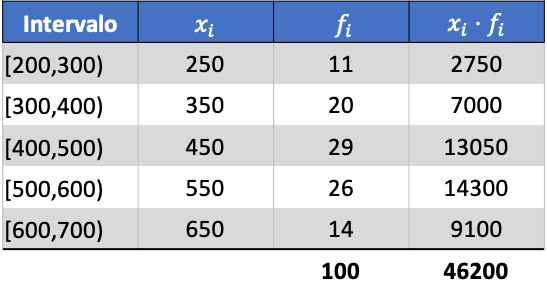
Quindi la media dei dati raggruppati sarà:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

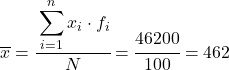
Ora che conosciamo il valore della media, dobbiamo aggiungere le seguenti tre colonne alla tabella dei dati:

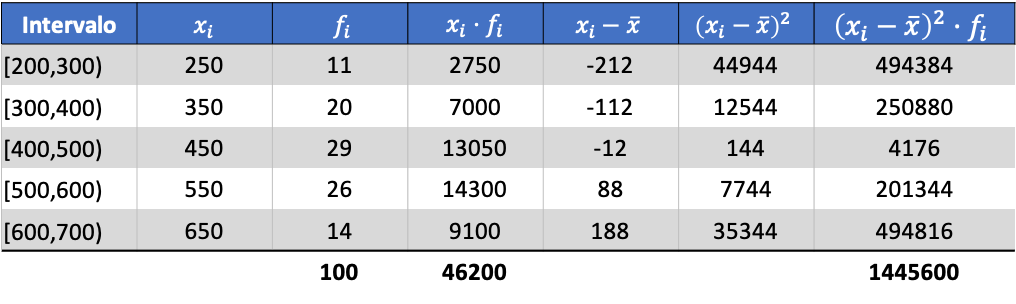
esercizio risolto di deviazione standard o deviazione standard per dati raggruppati

Quindi la deviazione standard dei dati raggruppati sarà il risultato della radice quadrata del totale dell’ultima colonna divisa per il numero totale di osservazioni:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

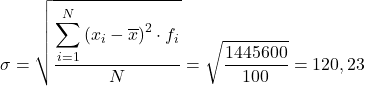
Deviazione e varianza standard (o tipica).

La relazione tra deviazione standard (o deviazione tipica) e varianza è che la deviazione standard è la radice quadrata della varianza.

Quindi, se conosciamo il valore della varianza di un set di dati, possiamo facilmente calcolare la deviazione standard prendendo la radice quadrata. Oppure, al contrario, se conosciamo la deviazione standard, possiamo trovare la varianza elevando al quadrato il valore.

$Var(X)=\sigma^2$

Infatti, la varianza può essere rappresentata semplicemente utilizzando il simbolo della deviazione standard quadrata. Pertanto, il simbolo della varianza della popolazione è sigma quadrato (σ ² ) e il simbolo della varianza campionaria è s quadrato (s ² ).

Inoltre, i concetti di deviazione standard e varianza hanno un’interpretazione simile, poiché entrambi mostrano la dispersione di una serie di dati statistici.

Proprietà della deviazione standard (o deviazione standard)

La deviazione standard ha le seguenti proprietà:

La deviazione standard di un campione di dati non può essere negativa.

$\sigma \ge 0$

La deviazione standard sarà zero se tutti i dati sono uguali.

$\sigma =0$

Se a tutti i dati viene aggiunto un termine costante, il valore della deviazione standard non cambia.

$\sigma (X+k)=\sigma (X)$

Se tutti i dati vengono moltiplicati per un numero, la deviazione standard verrà moltiplicata per il valore assoluto di tale numero.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

La deviazione standard della somma di due variabili casuali è uguale alla radice quadrata della somma delle varianze delle variabili più il doppio della covarianza tra le due variabili.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Se conosciamo le deviazioni standard delle diverse distribuzioni (σ _i ) e il loro numero di dati (n _i ), possiamo calcolare la deviazione standard totale applicando la seguente formula:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più