Come interpretare una deviazione standard pari a zero
In statistica, la deviazione standard viene utilizzata per misurare la distribuzione dei valori in un campione.
Possiamo utilizzare la seguente formula per calcolare la deviazione standard di un dato campione:
√ Σ(x i – x bar ) 2 / (n-1)
Oro:
- Σ: Un simbolo che significa “somma”
- x i : l’i -esimo valore del campione
- x bar : Il campione significa
- n: la dimensione del campione
Più alto è il valore della deviazione standard, più i valori sono dispersi in un campione .
Più basso è il valore della deviazione standard, più i valori sono raggruppati insieme.
Se la deviazione standard di un campione è zero, significa che tutti i valori nel campione sono esattamente gli stessi.
In altre parole, non vi è alcun divario tra i valori.
L’esempio seguente mostra come interpretare nella pratica una deviazione standard pari a zero.
Esempio: come interpretare una deviazione standard pari a zero
Supponiamo di raccogliere un semplice campione casuale di 10 lucertole e di misurare la loro lunghezza (in pollici):
Lunghezze : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7
La lunghezza media delle lucertole nel campione è di 7 pollici.
Sapendo questo, possiamo calcolare la/e deviazione/i standard campionaria/e per questo set di dati:
- s = √ Σ(x i – x bar ) 2 / (n-1)
- s = √ ((7 – 7) 2 + (7 – 7) 2 + (7 – 7) 2 + … + (7 – 7) 2 / (10-1)
- s = √ 0 2 + 0 2 + 0 2 + … + 0 2 / 9
- s = 0
La deviazione standard del campione risulta essere 0 .
Poiché ogni lucertola ha esattamente la stessa lunghezza, la distribuzione dei valori nel set di dati è esattamente zero.
La deviazione standard sarà mai pari a zero nel mondo reale?
È del tutto possibile che un set di dati del mondo reale abbia una deviazione standard pari a zero, ma è raro.
Lo scenario più probabile in cui potresti riscontrare una deviazione standard pari a zero sarebbe quando raccogli piccoli campioni per eventi rari.
Ad esempio, supponiamo di raccogliere dati sul numero di incidenti stradali in un periodo di una settimana in una determinata città.
È del tutto possibile che raccogliate i seguenti dati:
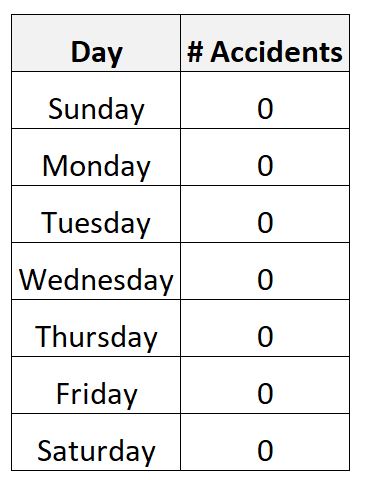
In questo scenario, il numero medio di incidenti giornalieri sarebbe pari a zero e anche la deviazione standard sarebbe pari a zero.
O forse raccogli i seguenti dati sul numero di vendite mensili di un prodotto costoso per un’azienda in un periodo di 6 mesi:
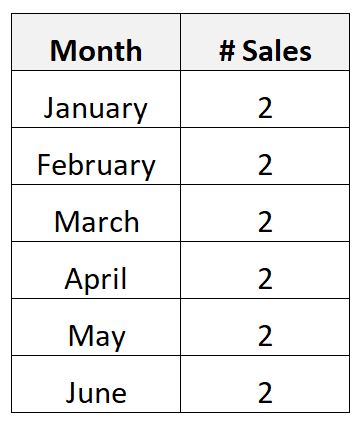
Poiché il prodotto è così costoso, si scopre che l’azienda ne vende esattamente solo due al mese.
In questo scenario, il numero medio di prodotti mensili venduti è due e la deviazione standard dei prodotti mensili venduti è zero.
Ogni volta che incontri una deviazione standard pari a zero in un set di dati reale, sappi solo che significa che ogni valore nel set di dati è esattamente lo stesso.
Risorse addizionali
Le seguenti esercitazioni forniscono informazioni aggiuntive sulla deviazione standard nelle statistiche:
Perché la deviazione standard è importante?
Deviazione standard ed errore standard: qual è la differenza?
Deviazione standard e intervallo interquartile: qual è la differenza?
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più