Deviazione standard relativa
Questo articolo spiega come calcolare la deviazione standard relativa. Scoprirai cos’è la deviazione standard relativa, qual è la sua formula e un esercizio risolto passo dopo passo.
Qual è la deviazione standard relativa?
La deviazione standard relativa è una misura statistica che indica la dispersione di un set di dati rispetto alla sua media. La deviazione standard relativa viene calcolata dividendo la deviazione standard dei dati per la sua media.
La deviazione standard relativa è espressa in percentuale e il suo valore sarà sempre positivo.
L’interpretazione della deviazione standard relativa viene utilizzata per mostrare la dispersione di un campione di dati. Maggiore è il valore della deviazione standard relativa, maggiore è la dispersione dei dati. E quanto più piccola è la deviazione standard relativa, tanto più i dati si avvicinano alla loro media.
Generalmente, l’acronimo RSD viene utilizzato come simbolo per la deviazione standard relativa.
Formula della deviazione standard relativa
La deviazione standard relativa è uguale alla deviazione standard divisa per la media moltiplicata per 100. Pertanto, per calcolare la deviazione standard relativa, è necessario prima determinare la deviazione standard e la media aritmetica, quindi dividere le due misurazioni statistiche e infine moltiplicare per 100.
In altre parole, la formula per la deviazione standard relativa è:
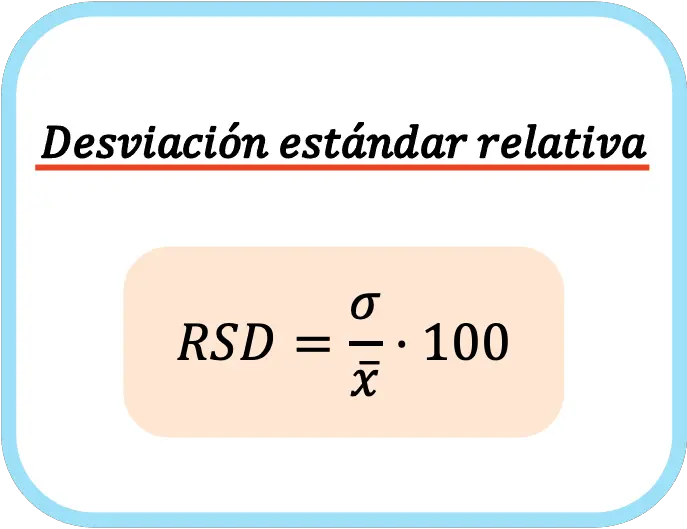
Quando si calcola la deviazione standard relativa, questa viene moltiplicata per cento per esprimere il valore in percentuale.
Esempio di calcolo della deviazione standard relativa
Dopo aver esaminato la definizione di deviazione standard relativa e la sua formula, di seguito puoi vedere un esempio concreto di come viene calcolata la deviazione standard relativa.
- Calcolare la deviazione standard relativa del seguente set di dati statistici:
4, 1, 3, 9, 12, 2, 5, 8, 3, 6
Per prima cosa dobbiamo trovare la deviazione standard dei dati:
In secondo luogo, calcoliamo la media aritmetica dei dati:
Una volta che conosciamo la deviazione standard e la media aritmetica delle serie di dati, utilizziamo la formula della deviazione standard relativa.
Infine, sostituiamo i valori calcolati nella formula e calcoliamo la deviazione standard relativa:
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più