Come calcolare la deviazione standard relativa in excel

La deviazione standard relativa è una misura della deviazione standard del campione dalla media campionaria per un dato set di dati.

Viene calcolato come segue:

Deviazione standard relativa = s/ x * 100%

Oro:

• s: deviazione standard campionaria
• x : media campionaria

Questa metrica ci dà un’idea di quanto strettamente le osservazioni siano raggruppate attorno alla media.

Ad esempio, supponiamo che la deviazione standard di un set di dati sia 4. Se la media è 400, la deviazione standard relativa è 4/400 * 100% = 1%. Ciò significa che le osservazioni sono strettamente raggruppate attorno alla media.

Tuttavia, un set di dati con una deviazione standard di 40 e una media di 400 avrà una deviazione standard relativa del 10%. Ciò significa che le osservazioni sono molto più distribuite attorno alla media rispetto al set di dati precedente.

Questo tutorial fornisce un esempio di calcolo della deviazione standard relativa in Excel.

Esempio: deviazione standard relativa in Excel

Supponiamo di avere il seguente set di dati in Excel:

Le seguenti formule mostrano come calcolare la media del campione, la deviazione standard del campione e la deviazione standard relativa del campione del set di dati:

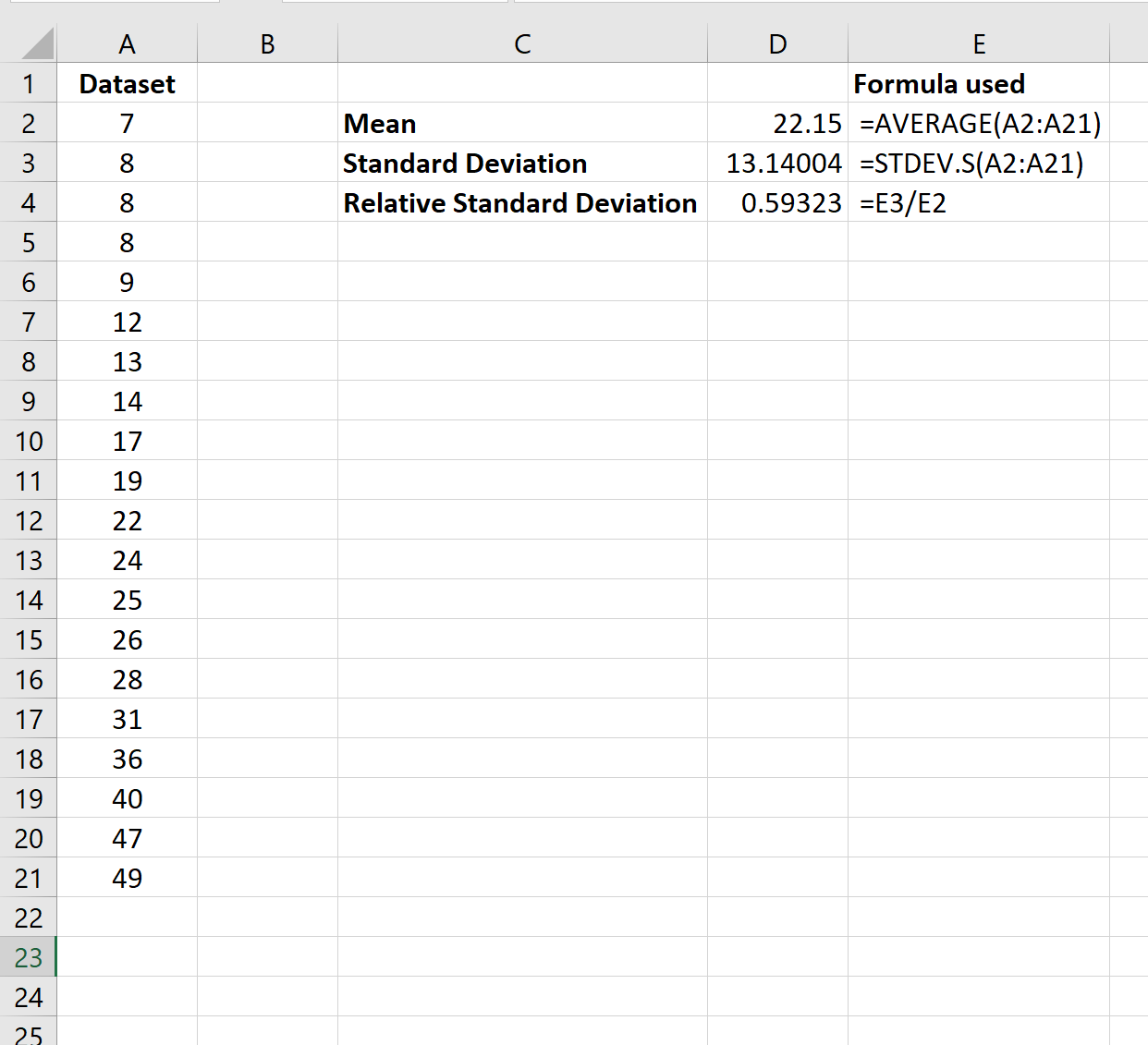
La deviazione standard relativa risulta essere 0,59 .

Questo ci dice che la deviazione standard del set di dati è pari al 59% della dimensione media del set di dati. Questo numero è piuttosto grande, indicando che i valori sono abbastanza distribuiti attorno alla media campionaria.

Se disponiamo di più set di dati, possiamo utilizzare la stessa formula per calcolare la deviazione standard relativa (RSD) per ciascun set di dati e confrontare le RSD tra i set di dati:

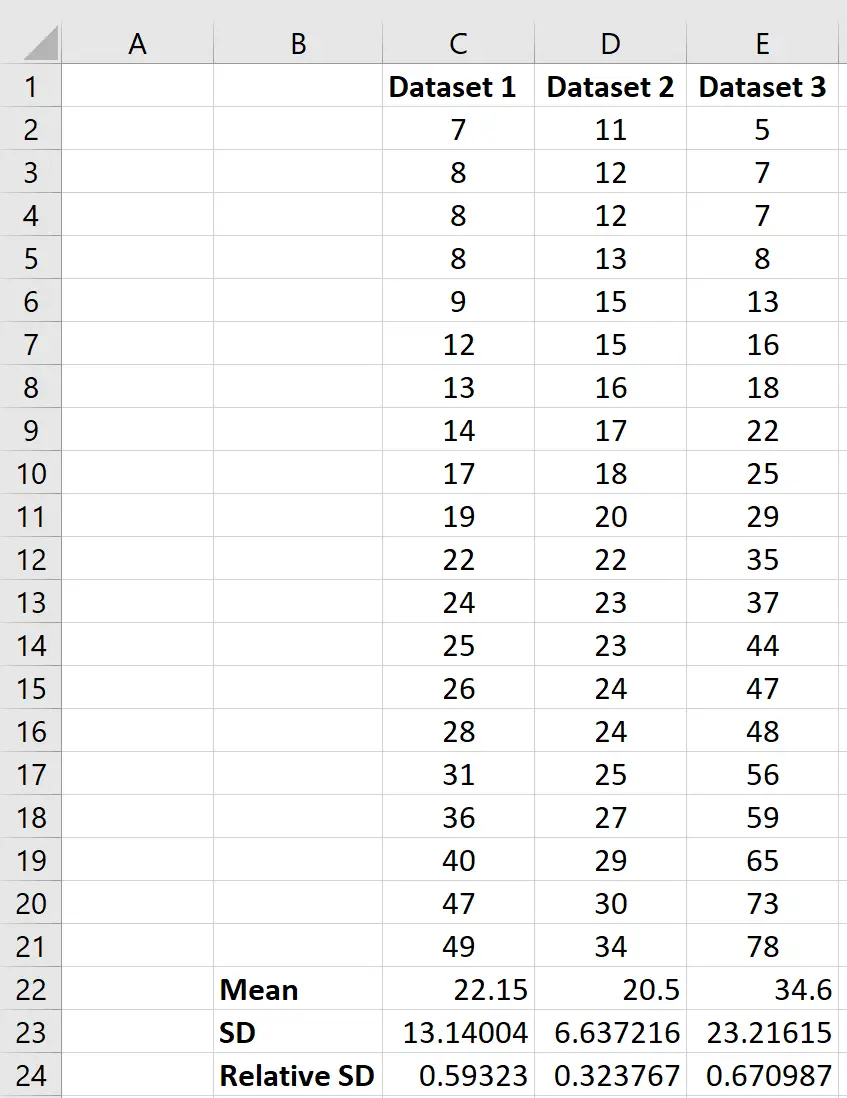
Possiamo vedere che il set di dati 3 ha la deviazione standard relativa più grande, indicando che i valori in questo set di dati sono i più dispersi dalla media del set di dati.

Al contrario, possiamo vedere che il set di dati 2 ha la deviazione standard relativa più piccola, indicando che i valori in questo set di dati sono meno distanti dalla media di questo particolare set di dati.

Puoi trovare altri tutorial su Excel qui .