Deviazione standard ed errore standard: qual è la differenza?

Due termini che gli studenti spesso confondono in statistica sono deviazione standard ed errore standard .

La deviazione standard misura la distribuzione dei valori in un set di dati.

L’ errore standard è la deviazione standard della media di campioni ripetuti di una popolazione.

Vediamo un esempio per illustrare chiaramente questa idea.

Esempio: deviazione standard rispetto all’errore standard

Supponiamo di misurare il peso di 10 tartarughe diverse.

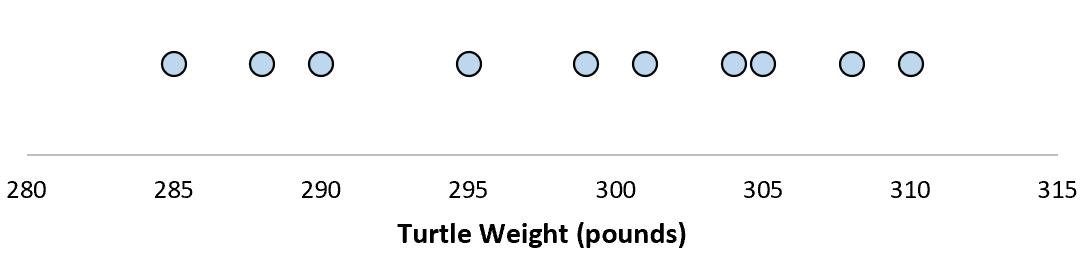
Per questo campione di 10 tartarughe, possiamo calcolare la media campionaria e la deviazione standard campionaria:

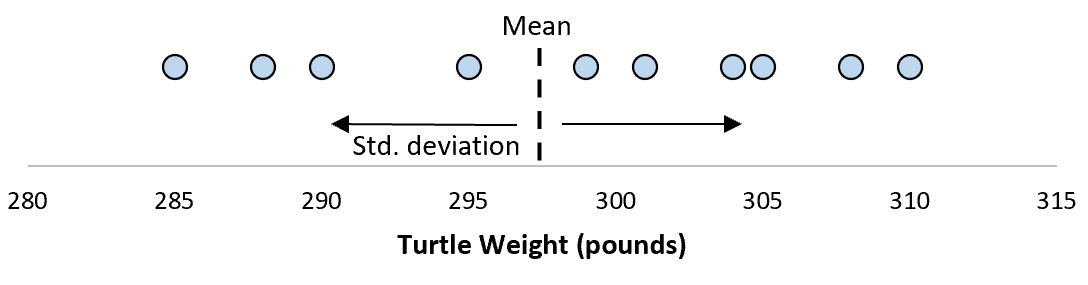
Supponiamo che la deviazione standard sia 8,68. Questo ci dà un’idea della distribuzione del peso di queste tartarughe.

Ma supponiamo di raccogliere un altro semplice campione casuale di 10 tartarughe e di effettuare anche le loro misurazioni.

È più che probabile che questo campione di 10 tartarughe avrà una media e una deviazione standard leggermente diverse, anche se provengono dalla stessa popolazione:

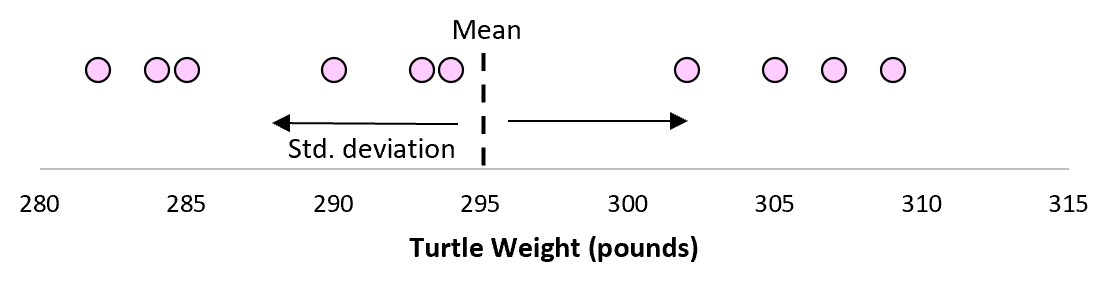
Ora, se immaginiamo di prendere campioni ripetuti dalla stessa popolazione e di registrare la media campionaria e la deviazione standard campionaria per ciascun campione:

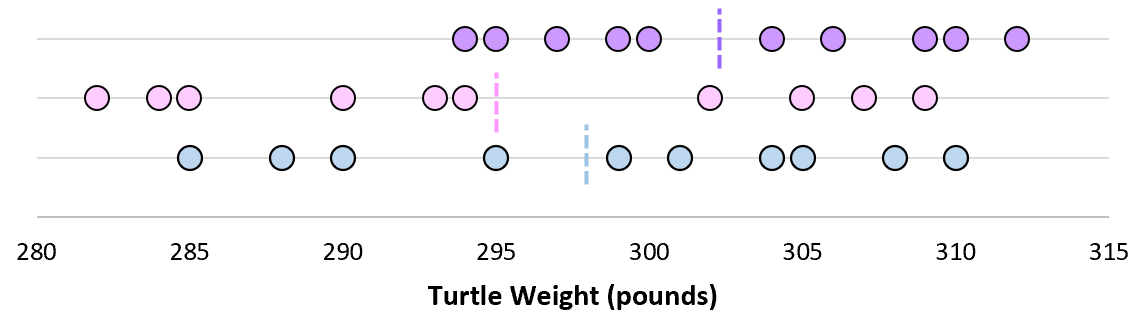
Immaginiamo ora di tracciare ciascuna media campionaria sulla stessa riga:

La deviazione standard di queste medie è chiamata errore standard.

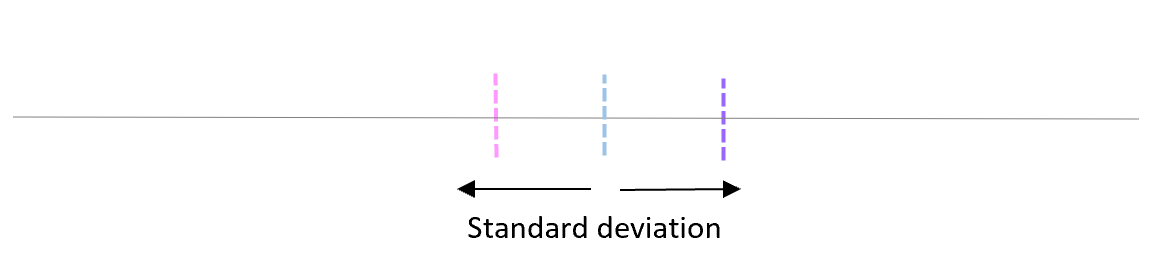
La formula per calcolare effettivamente l’errore standard è:

Errore standard = s/ √ n

Oro:

• s: deviazione standard campionaria
• n: dimensione del campione

Qual è lo scopo di utilizzare l’errore standard?

Quando calcoliamo la media di un dato campione, in realtà non stiamo cercando di conoscere la media di quel particolare campione, ma piuttosto la media della popolazione più ampia da cui proviene il campione.

Tuttavia, utilizziamo campioni perché è molto più semplice raccogliere dati per essi che per un’intera popolazione.

E, naturalmente, la media campionaria varia da campione a campione, quindi utilizziamo l’ errore standard della media come modo per misurare la precisione della nostra stima della media.

Noterai nella formula per il calcolo dell’errore standard che all’aumentare della dimensione del campione (n), l’errore standard diminuisce:

Errore standard = s/ √ n

Ciò dovrebbe avere senso, perché campioni più grandi riducono la variabilità e aumentano la possibilità che la nostra media campionaria sia più vicina alla media reale della popolazione.

Quando utilizzare la deviazione standard rispetto all’errore standard

Se vogliamo semplicemente misurare la distribuzione dei valori in un set di dati, possiamo utilizzare la deviazione standard .

Tuttavia, se vogliamo quantificare l’incertezza attorno a una stima della media, possiamo utilizzare l’ errore standard della media .

A seconda del tuo scenario specifico e di ciò che stai cercando di ottenere, puoi scegliere di utilizzare la deviazione standard o l’errore standard.