Come calcolare dfbetas in r

In statistica, spesso vogliamo sapere quale influenza hanno le diverse osservazioni sui modelli di regressione.

Un modo per calcolare l’influenza delle osservazioni è utilizzare una metrica nota come DFBETAS , che ci indica l’effetto standardizzato su ciascun coefficiente della rimozione di ogni singola osservazione.

Questa metrica ci dà un’idea dell’influenza di ciascuna osservazione su ciascuna stima di coefficiente in un dato modello di regressione.

Questo tutorial mostra un esempio passo passo di come calcolare e visualizzare DFBETAS per ogni osservazione in un modello in R.

Passaggio 1: creare un modello di regressione

Innanzitutto, creeremo un modello di regressione lineare multipla utilizzando il set di dati mtcars integrato in R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Passaggio 2: calcolare DFBETAS per ciascuna osservazione

Successivamente, utilizzeremo la funzione integrata dfbetas() per calcolare i valori DFBETAS per ciascuna osservazione nel modello:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Per ogni osservazione, possiamo vedere la differenza nella stima del coefficiente per l’origine, la variabile disp e la variabile hp che si verifica quando rimuoviamo quella particolare osservazione.

In generale, si considera che un’osservazione abbia una forte influenza sulla stima di un dato coefficiente se ha un valore DBETAS maggiore di una soglia pari a 2/√ n dove n è il numero di osservazioni.

In questo esempio, la soglia sarebbe 0,3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Passaggio 3: visualizzare i DFBETAS

Infine, possiamo creare grafici per visualizzare il valore DFBETAS per ciascuna osservazione e per ciascun predittore nel modello:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

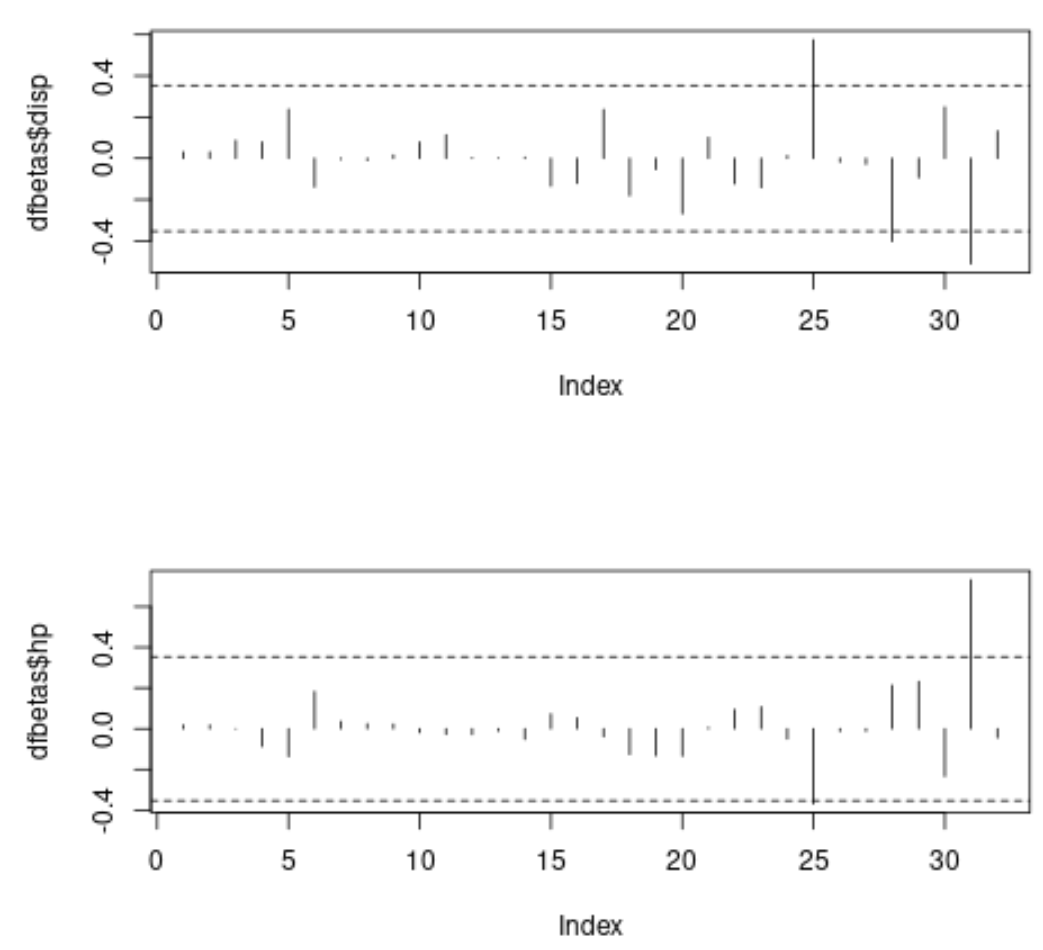
In ogni grafico, l’asse x mostra l’indice di ogni osservazione nel set di dati e il valore y mostra il DFBETAS corrispondente per ogni osservazione e ogni predittore.

Nel primo grafico possiamo vedere che tre osservazioni superano il valore di soglia assoluto di 0,3535534 e nel secondo grafico possiamo vedere che due osservazioni superano il valore di soglia assoluto.

Potremmo scegliere di studiare queste osservazioni più da vicino per determinare se hanno un’influenza eccessiva sulla stima dei coefficienti del modello.

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come calcolare le statistiche sulla leva finanziaria in R
Come calcolare DFFIT in R