Come interpretare i grafici diagnostici in r

I modelli di regressione lineare vengono utilizzati per descrivere la relazione tra una o più variabili predittive e una variabile di risposta.

Tuttavia, una volta adattato un modello di regressione, è una buona idea produrre anche grafici diagnostici per analizzare i residui del modello e garantire che un modello lineare sia appropriato da utilizzare per i dati particolari con cui stiamo lavorando.

Questo tutorial spiega come creare e interpretare grafici diagnostici per un determinato modello di regressione in R.

Esempio: creare e interpretare grafici diagnostici in R

Supponiamo di adattare un semplice modello di regressione lineare utilizzando le “ore studiate” per prevedere il “voto dell’esame” degli studenti in una determinata classe:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Possiamo utilizzare il comando plot() per produrre quattro grafici diagnostici per questo modello di regressione:

 #produce diagnostic plots for regression model
plot(model)

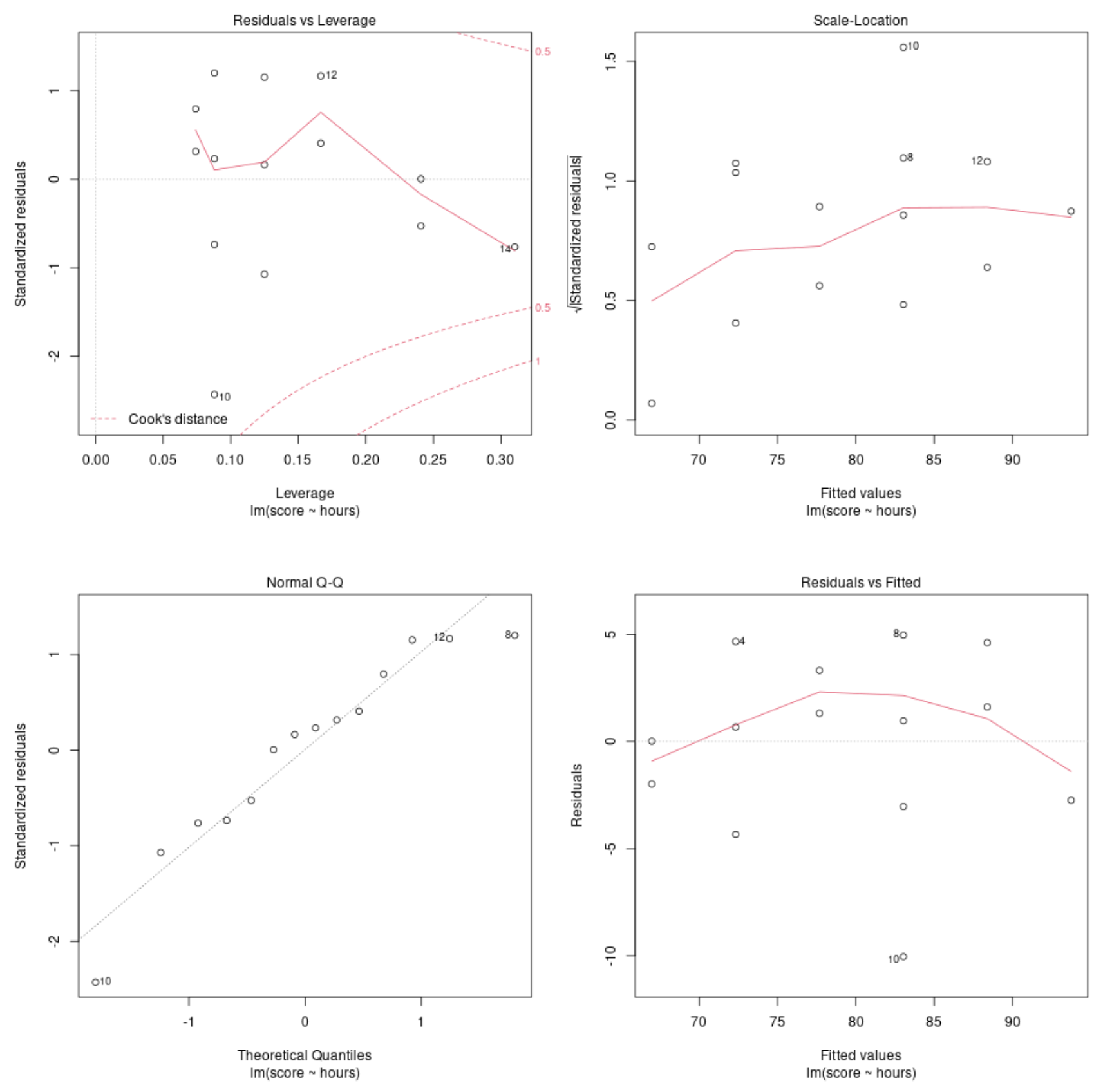
Grafico diagnostico n. 1: residui vs. Grafico della leva finanziaria

Questo grafico viene utilizzato per identificare le osservazioni influenti. Se qualche punto su questo grafico non rientra nella distanza di Cook (le linee tratteggiate), allora questa è un’osservazione influente.

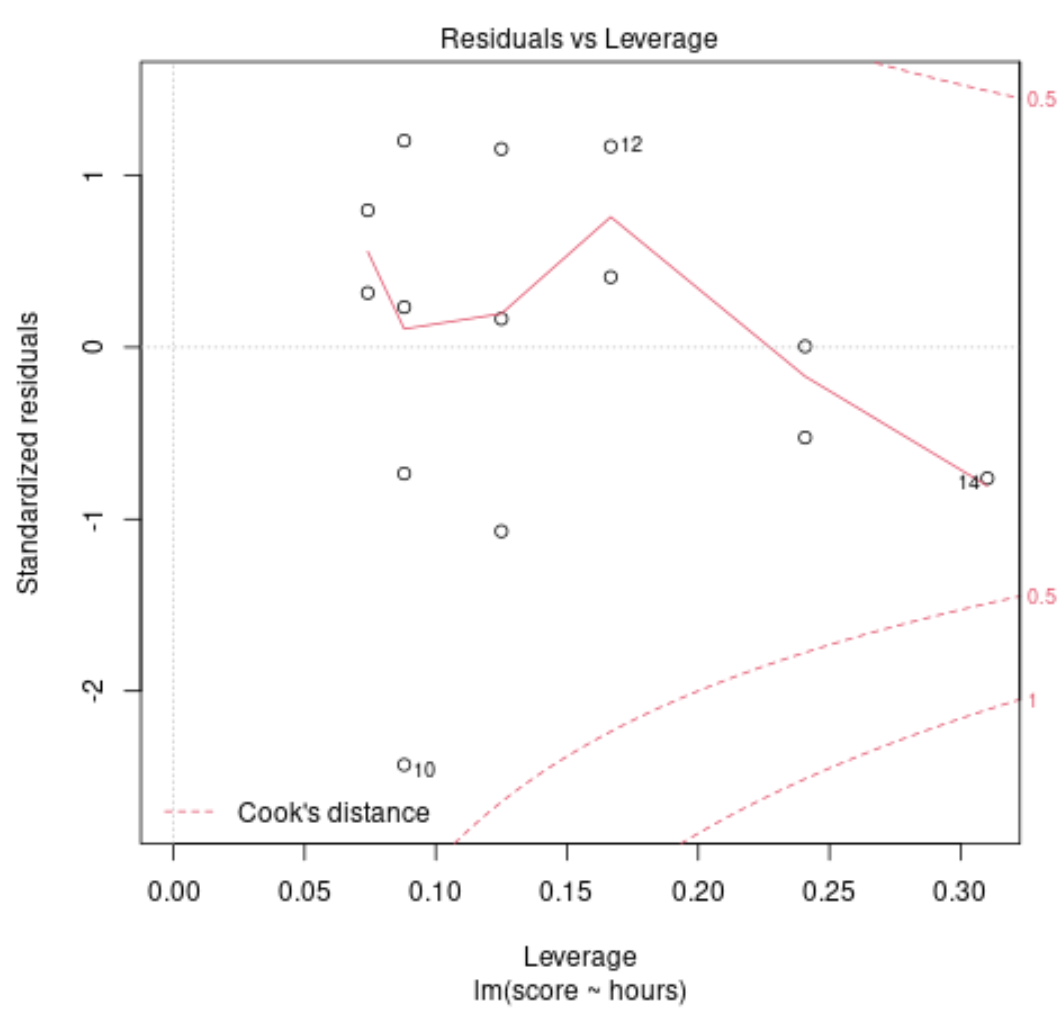
Nel nostro esempio, possiamo vedere che l’osservazione n. 10 è la più vicina al limite della distanza di Cook, ma non cade al di fuori della linea tratteggiata. Ciò significa che non ci sono punti eccessivamente influenti nel nostro set di dati.

Grafico diagnostico n. 2: diagramma di scala e posizione

Questo grafico viene utilizzato per verificare l’ipotesi di uguaglianza della varianza (detta anche “omoschedasticità”) tra i residui del nostro modello di regressione. Se la linea rossa è approssimativamente orizzontale sul grafico, probabilmente è soddisfatta l’ipotesi di uguale varianza.

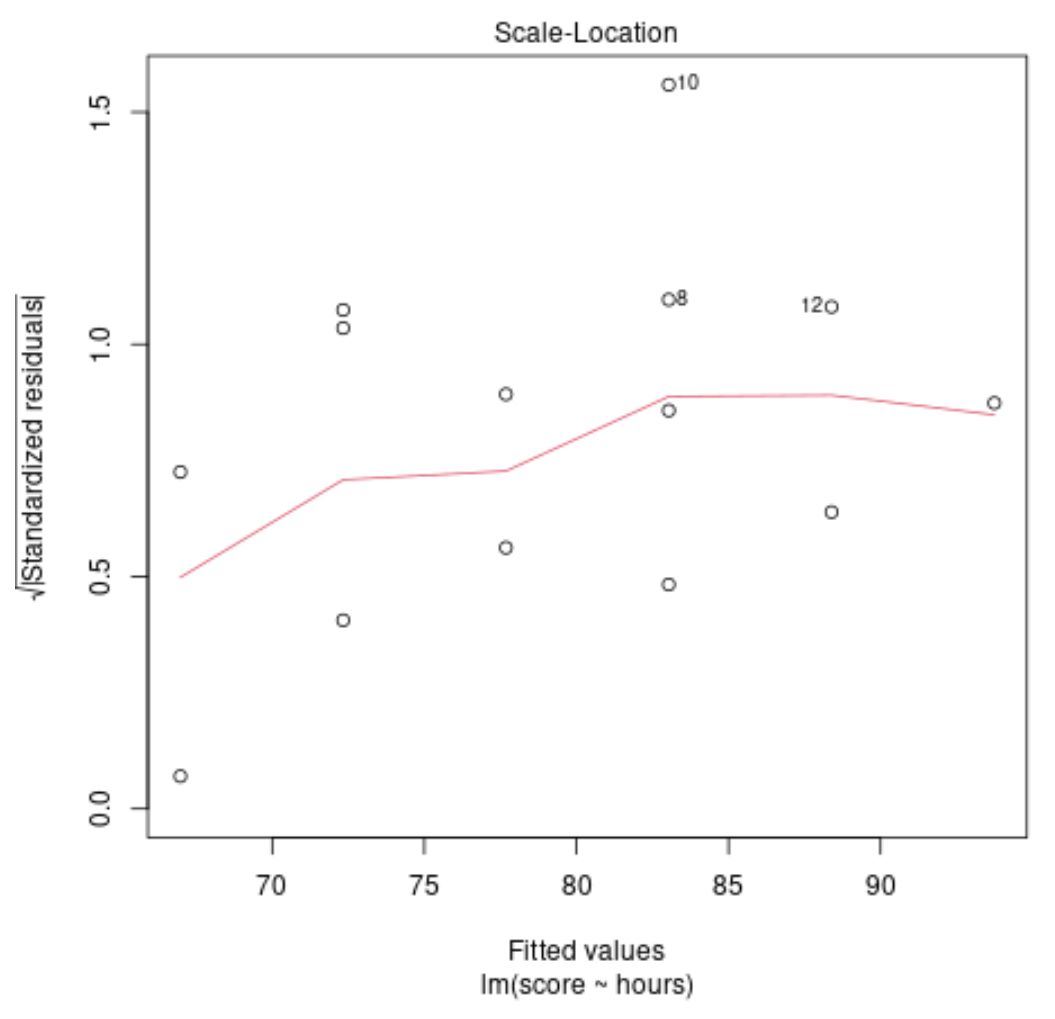
Nel nostro esempio, possiamo vedere che la linea rossa non è esattamente orizzontale sulla trama, ma non devia troppo in nessun punto. Probabilmente affermiamo che in questo caso l’ipotesi di eguale varianza non è violata.

Correlato: Comprensione dell’eteroschedasticità nell’analisi di regressione

Traccia diagnostica n. 3: traccia QQ normale

Questo grafico viene utilizzato per determinare se i residui del modello di regressione sono distribuiti normalmente. Se i punti su questo grafico si trovano approssimativamente lungo una linea diagonale retta, allora possiamo supporre che i residui siano distribuiti normalmente.

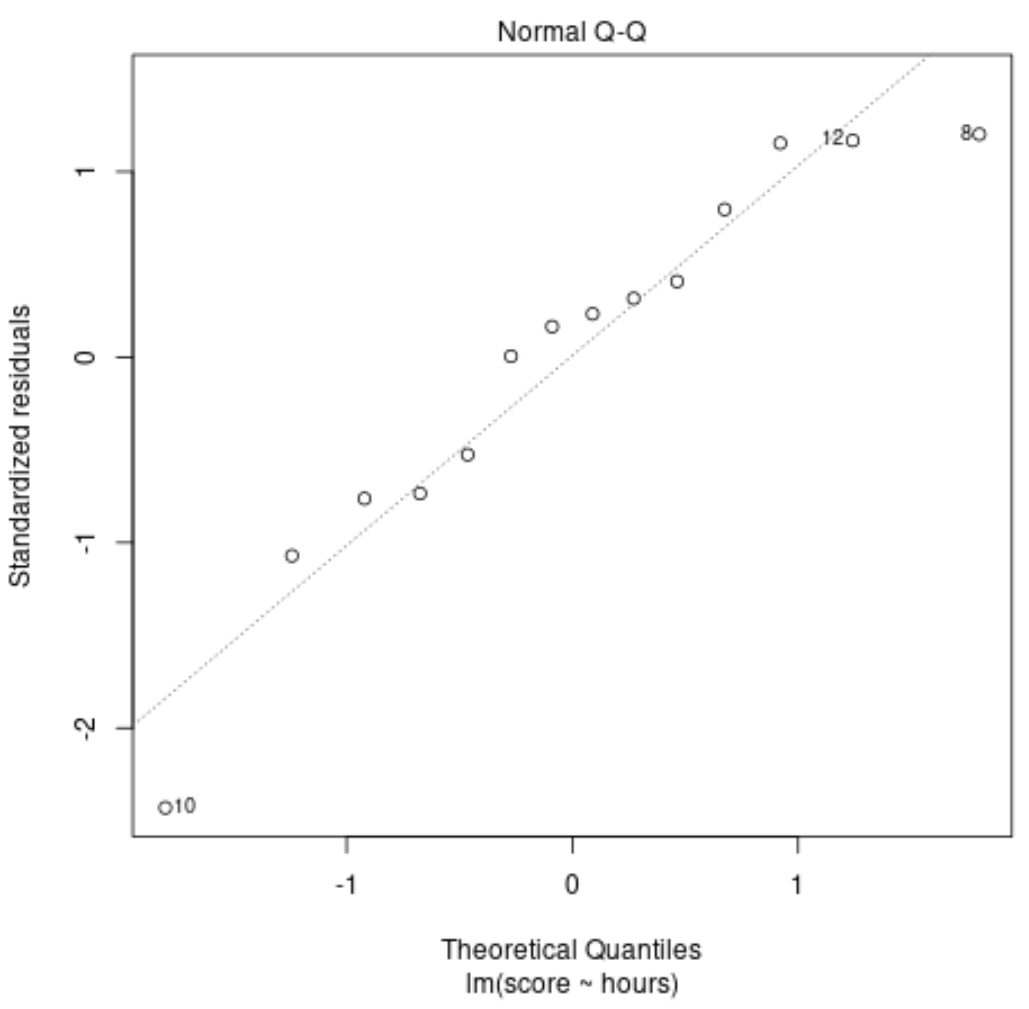
Nel nostro esempio possiamo vedere che i punti si trovano all’incirca lungo la retta diagonale. Le osservazioni n. 10 e n. 8 si discostano leggermente dalla linea alle estremità, ma non abbastanza per dichiarare che i residui non sono distribuiti normalmente.

Trama diagnostica n. 4: Residui vs. Trama modificata

Questo grafico viene utilizzato per determinare se i residui presentano modelli non lineari. Se la linea rossa al centro del grafico è approssimativamente orizzontale, possiamo supporre che i residui seguano uno schema lineare.

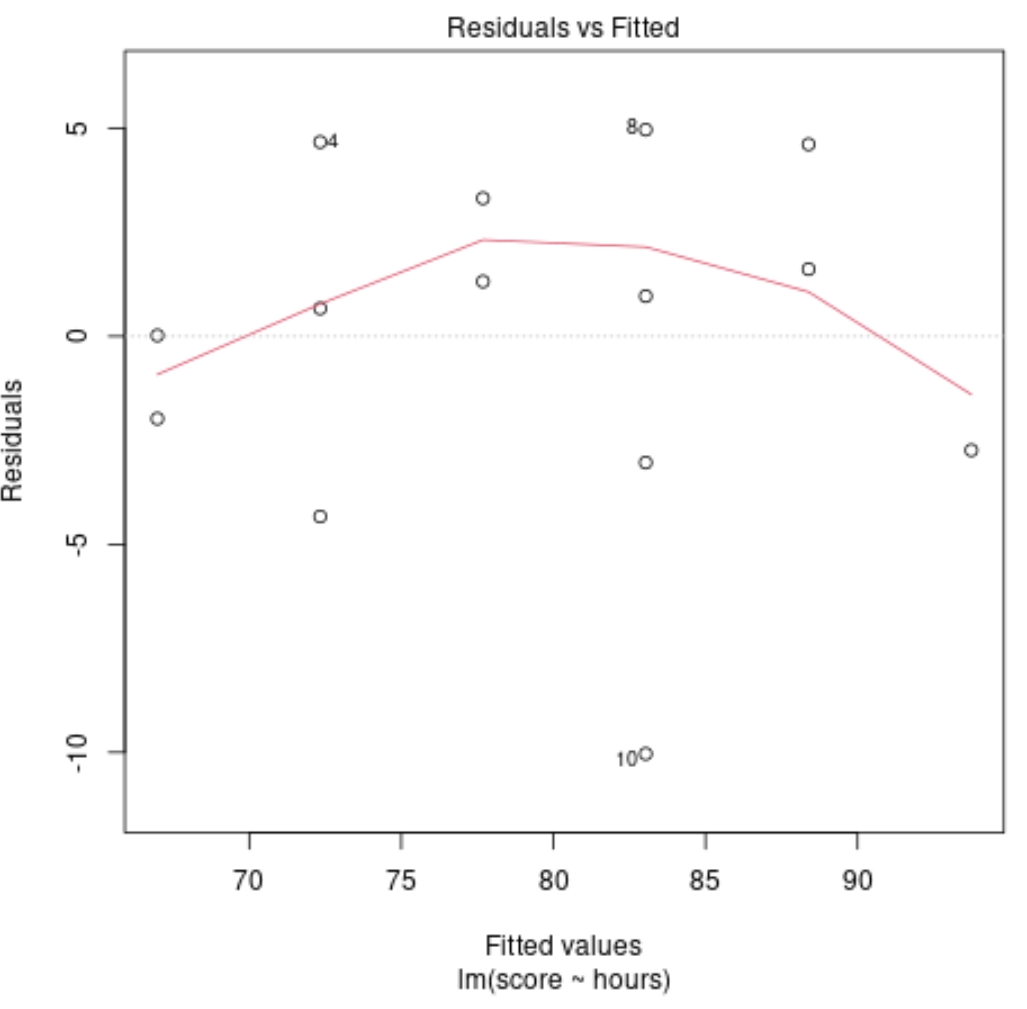
Nel nostro esempio possiamo vedere che la linea rossa si discosta da una linea orizzontale perfetta ma non in modo significativo. Probabilmente stiamo affermando che i residui seguono uno schema approssimativamente lineare e che un modello di regressione lineare è appropriato per questo set di dati.

Risorse addizionali

Le quattro ipotesi della regressione lineare
Cosa sono i residui in statistica?
Come creare una trama residua in R
Come interpretare un grafico di scala e posizione