La differenza meno significativa di fisher: definizione + esempio

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Le ipotesi utilizzate in un’ANOVA sono le seguenti:

H ₀ : Le medie sono uguali per ciascun gruppo.

H _A : Almeno uno dei modi è diverso dagli altri.

Se il valore p dell’ANOVA è inferiore a un certo livello di significatività (come α = 0,05), possiamo rifiutare l’ipotesi nulla e concludere che almeno una delle medie del gruppo è diversa dalle altre.

Ma per sapere esattamente quali gruppi sono diversi tra loro, dobbiamo fare un test post-hoc.

Un test post hoc comunemente utilizzato è il test delle differenze meno significative di Fisher .

Per eseguire questo test, calcoliamo prima la seguente statistica del test:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

Oro:

• t _.025 , _DFw : Il valore t-critico della tabella di distribuzione t con α = .025 e DF _w corrisponde ai gradi di libertà all’interno dei gruppi della tabella ANOVA.
• MS _W : quadrati medi all’interno dei gruppi nella tabella ANOVA.
• n ₁ , n ₂ : le dimensioni del campione di ciascun gruppo

Possiamo quindi confrontare la differenza media tra ciascun gruppo con questa statistica del test. Se il valore assoluto della differenza media tra due gruppi è maggiore della statistica test, possiamo dichiarare che esiste una differenza statisticamente significativa tra le medie del gruppo.

L’esempio seguente mostra come eseguire nella pratica il test della differenza meno significativa di Fisher.

Esempio: test della differenza di minima significatività di Fisher

Supponiamo che un professore voglia sapere se tre diverse tecniche di studio portano o meno a punteggi diversi nei test tra gli studenti. Per verificarlo, assegna in modo casuale 10 studenti a utilizzare ciascuna tecnica di studio e registra i risultati degli esami.

Nella tabella seguente sono riportati i risultati degli esami di ciascuno studente in base alla tecnica di studio utilizzata:

Il professore esegue un’ANOVA unidirezionale e ottiene i seguenti risultati:

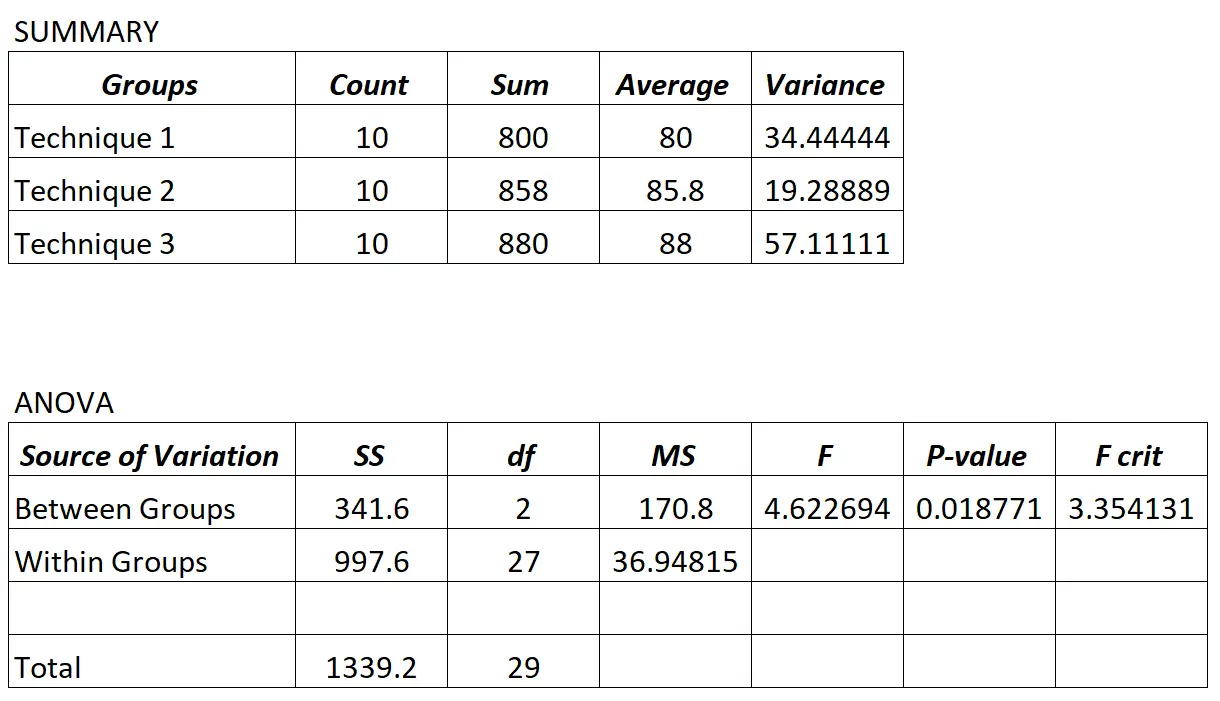
Poiché il valore p nella tabella ANOVA (0,018771) è inferiore a 0,05, possiamo concludere che tutti i punteggi medi degli esami tra i tre gruppi non sono uguali.

Quindi, possiamo eseguire il test delle differenze meno significative di Fisher per determinare quali medie di gruppo sono diverse.

Utilizzando i valori del risultato ANOVA, possiamo calcolare la statistica del test di Fisher come segue:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• LSD = 2,052 * √ 7,3896
• LSD = 5.578

Possiamo quindi calcolare la differenza media assoluta tra ciascun gruppo:

• Tecnica 1 contro Tecnica 2: |80 – 85.8| = 5,8
• Tecnica 1 contro Tecnica 3: |80 – 88| = 8
• Tecnica 2 contro Tecnica 3: |85.8 – 88| = 2,2

Le differenze medie assolute tra la tecnica 1 e la tecnica 2 e tra la tecnica 1 e la tecnica 3 sono maggiori delle statistiche del test di Fisher. Possiamo quindi concludere che queste tecniche portano a punteggi medi degli esami statisticamente significativi.

Possiamo anche concludere che non vi è alcuna differenza significativa nei punteggi medi degli esami tra la tecnica 2 e la tecnica 3.