Dimensione dell’effetto: cos’è e perché è importante
“La significatività statistica è la cosa meno interessante dei risultati. È necessario descrivere i risultati in termini di misure di grandezza: non solo un trattamento influisce sulle persone, ma quanto le influenza. -Gene V. Vetro
Nelle statistiche, utilizziamo spesso i valori p per determinare se esiste una differenza statisticamente significativa tra due gruppi.
Ad esempio, supponiamo di voler sapere se due diverse tecniche di studio portano a punteggi diversi nei test. Quindi, abbiamo un gruppo di 20 studenti che utilizza una tecnica di studio per prepararsi per un test mentre un altro gruppo di 20 studenti utilizza una tecnica di studio diversa. Quindi diamo a ogni studente lo stesso test.
Dopo aver eseguito un test t su due campioni per determinare una differenza nelle medie, troviamo che il valore p per il test è 0,001. Se utilizziamo un livello di significatività pari a 0,05, ciò significa che esiste una differenza statisticamente significativa tra i risultati medi dei due gruppi. Quindi, la tecnica di studio ha un impatto sui risultati del test.
Tuttavia, sebbene il valore p ci dica che lo studio della tecnica ha un impatto sui punteggi dei test, non ci dice l’ entità di tale impatto. Per capirlo, dobbiamo conoscere la dimensione dell’effetto .
Qual è la dimensione dell’effetto?
Una dimensione dell’effetto è un modo per quantificare la differenza tra due gruppi.
Mentre un valore p può dirci se esiste o meno una differenza statisticamente significativa tra due gruppi, una dimensione dell’effetto può dirci quanto è realmente grande quella differenza. In pratica, le dimensioni degli effetti sono molto più interessanti e utili da conoscere rispetto ai valori p.
Esistono tre modi per misurare la dimensione dell’effetto, a seconda del tipo di analisi che stai eseguendo:
1. Differenza media standardizzata
Quando si desidera studiare la differenza media tra due gruppi, il modo appropriato per calcolare la dimensione dell’effetto è utilizzare una differenza media standardizzata . La formula più popolare da utilizzare è nota come d di Cohen, che viene calcolata come segue:
D di Cohen = ( x1 – x2 )/ s
dove x 1 e x 2 sono le medie campionarie rispettivamente del gruppo 1 e del gruppo 2 e s è la deviazione standard della popolazione da cui sono stati estratti i due gruppi.
Utilizzando questa formula, la dimensione dell’effetto è facile da interpretare:
- Un d pari a 1 indica che le medie dei due gruppi differiscono di una deviazione standard.
- Un d pari a 2 significa che le medie del gruppo differiscono di due deviazioni standard.
- Un d pari a 2,5 indica che le due medie differiscono di 2,5 deviazioni standard e così via.
Un altro modo di interpretare la dimensione dell’effetto è: una dimensione dell’effetto di 0,3 significa che il punteggio della persona media nel Gruppo 2 è di 0,3 deviazioni standard superiore alla media della persona del gruppo 1 e quindi supera i punteggi del 62% di quelli del gruppo 1 . .
La tabella seguente mostra le diverse dimensioni degli effetti e i relativi percentili:
| Dimensione dell’effetto | Percentuale del gruppo 2 che sarebbe inferiore alla media delle persone del gruppo 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0.4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99,9% |
Maggiore è la dimensione dell’effetto, maggiore è la differenza tra l’individuo medio in ciascun gruppo.
In generale, un d pari o inferiore a 0,2 è considerato una dimensione dell’effetto piccola, un d pari a circa 0,5 è considerato una dimensione dell’effetto media e un d pari o superiore a 0,8 è considerato una dimensione dell’effetto grande.
Quindi, se le medie dei due gruppi non differiscono di almeno 0,2 deviazioni standard, la differenza è insignificante, anche se il valore p è statisticamente significativo.
2. Coefficiente di correlazione
Quando si desidera studiare la relazione quantitativa tra due variabili, il modo più comune per calcolare la dimensione dell’effetto è utilizzare il coefficiente di correlazione di Pearson . È una misura dell’associazione lineare tra due variabili X e Y. Ha un valore compreso tra -1 e 1 dove:
- -1 indica una correlazione lineare perfettamente negativa tra due variabili
- 0 indica alcuna correlazione lineare tra due variabili
- 1 indica una correlazione lineare perfettamente positiva tra due variabili
La formula per calcolare il coefficiente di correlazione di Pearson è piuttosto complessa, ma chi è interessato può trovarla qui .
Quanto più il coefficiente di correlazione si allontana da zero, tanto più forte è la relazione lineare tra due variabili. Questo può essere visto anche creando un semplice grafico a dispersione dei valori delle variabili X e Y.
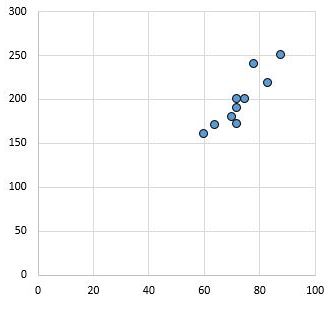
Ad esempio, il seguente grafico a dispersione mostra i valori di due variabili con un coefficiente di correlazione r = 0,94.
Questo valore è lontano da zero, indicando che esiste una forte relazione positiva tra le due variabili.
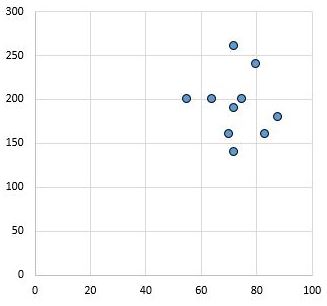
Al contrario, il seguente grafico a dispersione mostra i valori di due variabili che hanno un coefficiente di correlazione r = 0,03. Questo valore è vicino allo zero, indicando che non esiste praticamente alcuna relazione tra le due variabili.
In generale, la dimensione dell’effetto è considerata piccola se il valore del coefficiente di correlazione di Pearson r è circa 0,1, media se r è circa 0,3 e grande se r è pari o superiore a 0,5.
3. Rapporto di probabilità
Quando si desidera studiare le probabilità di successo in un gruppo di trattamento rispetto alle probabilità di successo in un gruppo di controllo, il modo più comune per calcolare la dimensione dell’effetto è utilizzare l’ odds ratio .
Supponiamo ad esempio di avere la seguente tabella:
| Dimensione dell’effetto | #Successo | #Scacchi |
|---|---|---|
| Gruppo di trattamento | HA | B |
| Gruppo di controllo | VS | D |
Il rapporto odd verrebbe calcolato come segue:
Rapporto di probabilità = (AD) / (BC)
Più l’odds ratio si allontana da 1, maggiore è la probabilità che il trattamento produca un effetto reale.
I vantaggi dell’utilizzo delle dimensioni degli effetti rispetto ai valori P
Le dimensioni degli effetti presentano diversi vantaggi rispetto ai valori p:
1. La dimensione dell’effetto ci aiuta a farci un’idea migliore di quanto sia grande la differenza tra due gruppi o di quanto sia forte l’associazione tra due gruppi. Un valore p può solo dirci se esiste o meno una differenza significativa o un’associazione significativa.
2. A differenza dei valori p, le dimensioni degli effetti possono essere utilizzate per confrontare quantitativamente i risultati di diversi studi condotti in contesti diversi. Per questo motivo, nelle meta-analisi vengono spesso utilizzate le dimensioni degli effetti.
3. I valori P possono essere influenzati da campioni di grandi dimensioni. Maggiore è la dimensione del campione, maggiore è il potere statistico di un test di ipotesi, consentendogli di rilevare anche piccoli effetti. Ciò può portare a valori p bassi, nonostante le dimensioni ridotte degli effetti che potrebbero non avere alcun significato pratico.
Un semplice esempio può illustrarlo chiaramente: supponiamo di voler sapere se due tecniche di studio portano a punteggi diversi nei test. Abbiamo un gruppo di 20 studenti che utilizzano una tecnica di studio mentre un altro gruppo di 20 studenti che utilizza una tecnica di studio diversa. Quindi diamo a ogni studente lo stesso test.
Il punteggio medio del gruppo 1 è 90,65 e il punteggio medio del gruppo 2 è 90,75 . La deviazione standard per il campione 1 è 2,77 e la deviazione standard per il campione 2 è 2,78 .
Quando eseguiamo un t-test indipendente a due campioni, risulta che la statistica del test è -0,113 e il valore p corrispondente è 0,91 . La differenza tra i punteggi medi dei test non è statisticamente significativa.
Tuttavia, considera se le dimensioni dei due campioni fossero entrambe 200 , ma le medie e le deviazioni standard rimanessero esattamente le stesse.
In questo caso, un test t indipendente a due campioni rivelerebbe che la statistica del test è -1,97 e il valore p corrispondente è appena inferiore a 0,05 . La differenza tra i punteggi medi dei test è statisticamente significativa.
Il motivo di fondo per cui campioni di grandi dimensioni possono portare a conclusioni statisticamente significative è dovuto alla formula utilizzata per calcolare le statistiche del t- test:
statistica del test t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Si noti che quando n 1 e n 2 sono piccoli, il denominatore intero della statistica t -test è piccolo. E quando dividi per un numero piccolo, ottieni un numero grande. Ciò significa che la statistica del test t sarà ampia e il valore p corrispondente sarà piccolo, portando così a risultati statisticamente significativi.
Qual è considerata una buona dimensione dell’effetto?
Una domanda che spesso gli studenti pongono è: quale è considerata una buona dimensione dell’effetto?
La risposta è breve: la dimensione dell’effetto non può essere “buona” o “cattiva” poiché misura semplicemente l’entità della differenza tra due gruppi o la forza dell’associazione tra due gruppi.
Tuttavia, possiamo utilizzare le seguenti regole empiriche per quantificare se l’entità di un effetto è piccola, media o grande:
D di Cohen:
- Un d pari o inferiore a 0,2 è considerato una dimensione dell’effetto piccola.
- Un d pari a 0,5 è considerato una dimensione dell’effetto media.
- Un d pari o superiore a 0,8 è considerato un effetto di grande dimensione.
Coefficiente di correlazione di Pearson
- Un valore assoluto di r attorno a 0,1 è considerato una dimensione dell’effetto piccola.
- Un valore assoluto di r intorno a 0,3 è considerato una dimensione dell’effetto media.
- Un valore assoluto di r maggiore di 0,5 è considerato un effetto di grande dimensione.
Tuttavia, la definizione di correlazione “forte” può variare da un campo all’altro. Fare riferimento a questo articolo per comprendere meglio cosa è considerata una forte correlazione tra diversi settori.