Una guida completa: il disegno fattoriale 2×4

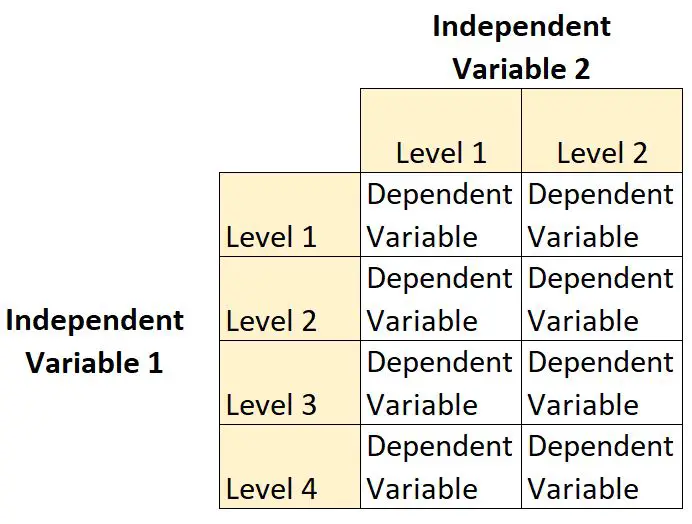
Un disegno fattoriale 2 × 4 è un tipo di disegno sperimentale che consente ai ricercatori di comprendere gli effetti di due variabili indipendenti su una singola variabile dipendente.

In questo tipo di progettazione, una variabile indipendente ha due livelli e l’altra variabile indipendente ha quattro livelli.

Ad esempio, supponiamo che un botanico voglia comprendere gli effetti della luce solare (nessuna, bassa, media o alta) e della frequenza di irrigazione (giornaliera o settimanale) sulla crescita di una determinata specie di piante.

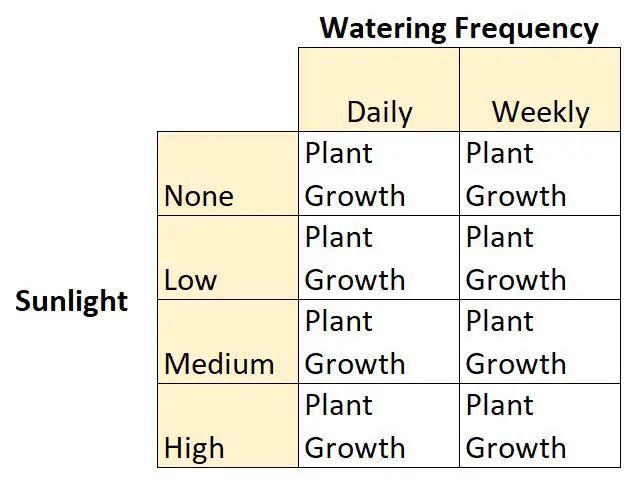
Questo è un esempio di disegno fattoriale 2 × 4 perché sono presenti due variabili indipendenti, una con due livelli e una con quattro livelli:

• Variabile indipendente n. 1: luce solare
  • Livelli: Nessuno, Basso, Medio, Alto
• Variabile indipendente n. 2: frequenza di irrigazione
  • Livelli: giornaliero, settimanale

E c’è una variabile dipendente: la crescita delle piante.

Lo scopo di un disegno fattoriale 2 × 4

Un disegno fattoriale 2×4 consente di analizzare i seguenti effetti:

Effetti principali: sono gli effetti che una singola variabile indipendente ha sulla variabile dipendente.

Ad esempio, nel nostro scenario precedente, potremmo analizzare i seguenti effetti principali:

• Principale effetto della luce solare sulla crescita delle piante.
  • Crescita media di tutte le piante che non hanno ricevuto luce solare.
  • Crescita media di tutte le piante che hanno ricevuto poca luce solare.
  • Crescita media di tutte le piante che hanno ricevuto luce solare media.
  • Crescita media di tutte le piante che hanno ricevuto un’elevata luce solare.
• Effetto principale della frequenza di irrigazione sulla crescita delle piante.
  • Crescita media di tutte le piante irrigate quotidianamente.
  • Crescita media di tutte le piante annaffiate ogni settimana.

Effetti di interazione: si verificano quando l’effetto di una variabile indipendente sulla variabile dipendente dipende dal livello dell’altra variabile indipendente.

Ad esempio, nel nostro scenario precedente, potremmo analizzare i seguenti effetti di interazione:

• L’effetto della luce solare sulla crescita delle piante dipende dalla frequenza dell’irrigazione?
• L’effetto della frequenza dell’irrigazione sulla crescita delle piante dipende dalla luce solare?

Come analizzare un disegno fattoriale 2×4

Possiamo eseguire un’ANOVA a due vie per verificare formalmente se le variabili indipendenti hanno o meno una relazione statisticamente significativa con la variabile dipendente.

Ad esempio, il codice seguente mostra come eseguire un’ANOVA bidirezionale per il nostro ipotetico scenario di fabbrica in R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ecco come interpretare il risultato ANOVA:

Effetto principale n. 1 (luce solare) : il valore p associato alla luce solare è <2e-16 . Poiché questo numero è inferiore a 0,05, significa che l’esposizione alla luce solare ha un effetto statisticamente significativo sulla crescita delle piante.

Effetto principale n. 2 (Acqua) : il valore p associato all’acqua è 0,016 . Poiché questo valore è inferiore a 0,05, significa che anche la frequenza di irrigazione ha un effetto statisticamente significativo sulla crescita delle piante.

Effetto di interazione : il valore p per l’interazione tra luce solare e acqua è 0,000061 . Poiché questo valore è inferiore a 0,05, significa che esiste un effetto di interazione tra la luce solare e l’acqua.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulla progettazione e sull’analisi sperimentale:

Una guida completa: il disegno fattoriale 2×2
Una guida completa: il disegno fattoriale 2×3
Che cos’è un’ANOVA fattoriale?