Distribuzione beta

Di Benjamin anderson Agosto 4, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è la distribuzione beta e a cosa serve. Allo stesso modo, potrai vedere il grafico della distribuzione beta e le proprietà di questo tipo di distribuzione di probabilità.

Qual è la distribuzione beta?

La distribuzione beta è una distribuzione di probabilità definita sull’intervallo (0,1) e parametrizzata da due parametri positivi: α e β. In altre parole, i valori della distribuzione beta dipendono dai parametri α e β.

Pertanto, la caratteristica principale della distribuzione beta è che la sua forma può essere controllata dai parametri α e β. Inoltre, la distribuzione beta viene utilizzata per definire variabili casuali il cui valore è compreso tra 0 e 1.

Esistono diverse notazioni per indicare che una variabile casuale continua è governata da una distribuzione beta, le più comuni sono:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

Nelle statistiche, la distribuzione beta ha applicazioni molto diverse. Ad esempio, la distribuzione beta viene utilizzata per studiare le variazioni percentuali in diversi campioni. Allo stesso modo, nella gestione dei progetti, la distribuzione beta viene utilizzata per eseguire l’analisi Pert.

Grafico della distribuzione beta

Considerando la definizione di distribuzione beta, di seguito sono tracciate la funzione di densità e la funzione di distribuzione di probabilità della distribuzione beta.

Di seguito puoi vedere come varia il grafico della funzione di densità della distribuzione beta a seconda dei parametri α e β.

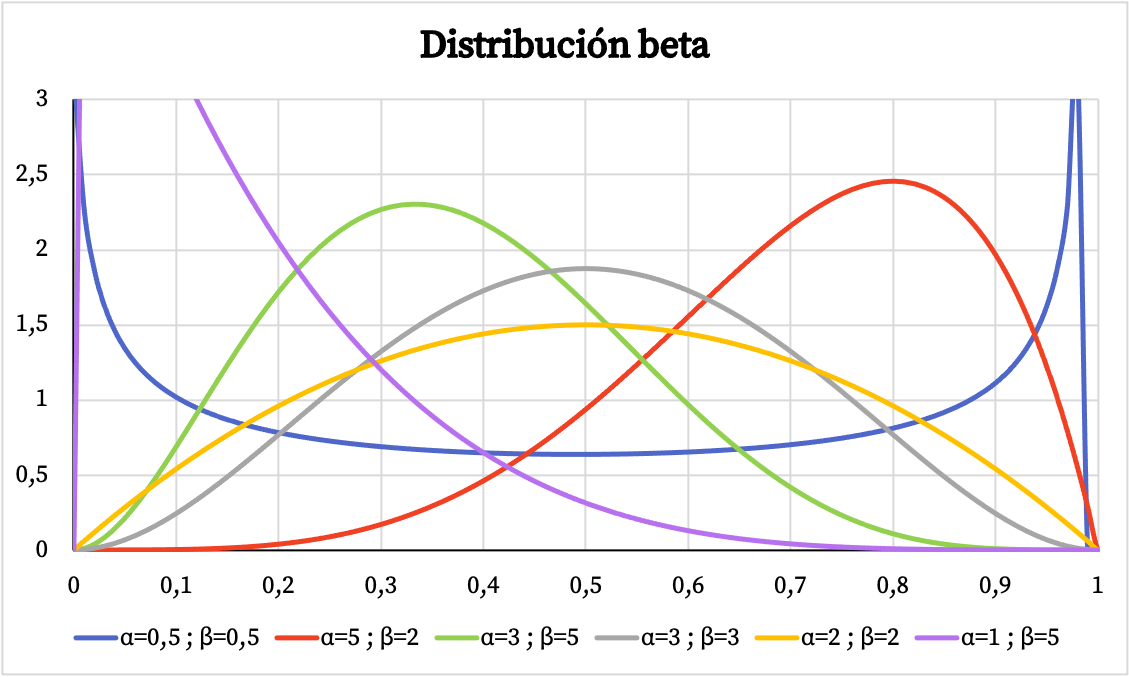
Allo stesso modo, qui sotto potete vedere la rappresentazione grafica della probabilità cumulativa della distribuzione beta in base ai parametri α e β.

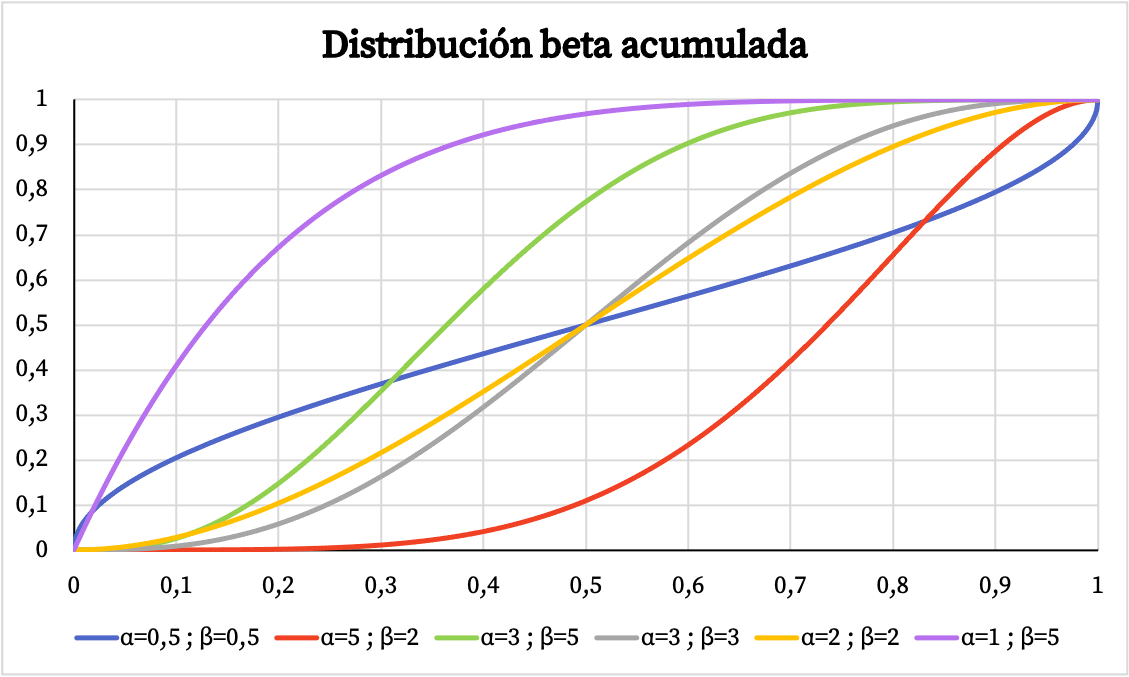
grafico di distribuzione beta cumulativa

Caratteristiche della distribuzione beta

In questa sezione vedremo quali sono le caratteristiche più importanti della distribuzione beta.

I parametri α e β della distribuzione beta sono numeri reali e positivi.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Il dominio della distribuzione beta varia da 0 a 1, i due estremi non sono inclusi.</li> </ul> <p class=$ $x\in (0,1)$

La media della distribuzione beta è uguale ad alfa diviso per la somma alfa più beta.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

La varianza della distribuzione beta può essere calcolata utilizzando la seguente formula:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Per valori di alfa e beta maggiori di 1 la modalità di distribuzione beta può essere facilmente trovata con la seguente espressione:

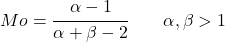
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”225″ style=”vertical-align: -16px;”></p> </p> <ul> <li> La funzione di densità della distribuzione beta è la seguente:</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Dove B(α,β) è la funzione beta, che è definita come:

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

La funzione di probabilità cumulativa della distribuzione beta è:

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Dove B(x;α,β) è la funzione beta incompleta, definita come:

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Se X è una variabile definita da una distribuzione beta, allora 1-X è una variabile definita da una distribuzione beta i cui parametri alfa e beta sono rispettivamente i parametri beta e alfa della distribuzione beta originale.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Se i parametri alfa e beta della distribuzione beta sono entrambi uguali a 1, allora la distribuzione è equivalente a una distribuzione uniforme dei parametri 0 e 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Qual è la distribuzione beta?

Grafico della distribuzione beta

Caratteristiche della distribuzione beta

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento