Distribuzione binomiale

Di Benjamin anderson Agosto 3, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è la distribuzione binomiale nelle statistiche e a cosa serve. Troverai quindi la definizione di distribuzione binomiale, esempi di distribuzioni binomiali e le proprietà di questo tipo di distribuzione di probabilità. Inoltre, potrai calcolare qualsiasi probabilità della distribuzione binomiale con un calcolatore online.

Qual è la distribuzione binomiale?

La distribuzione binomiale è una distribuzione di probabilità che conta il numero di successi durante l’esecuzione di una serie di esperimenti dicotomici indipendenti con una probabilità di successo costante.

In altre parole, la distribuzione binomiale è una distribuzione che descrive il numero di esiti positivi di una sequenza di prove Bernoulliane.

Ricorda che un test di Bernoulli è un esperimento che ha due possibili esiti: “successo” e “fallimento”. Pertanto, se la probabilità di “successo” è p , la probabilità di “fallimento” è q=1-p .

In generale il numero totale di esperimenti eseguiti è definito con il parametro n , mentre p è la probabilità di successo di ciascun esperimento. Pertanto, una variabile casuale che segue una distribuzione binomiale si scrive come segue:

$X\sim\text{Bin}(n,p)$

Si noti che in una distribuzione binomiale, lo stesso identico esperimento viene ripetuto n volte e gli esperimenti sono indipendenti l’uno dall’altro, quindi la probabilità di successo di ciascun esperimento è la stessa (p) .

La distribuzione binomiale può anche essere chiamata distribuzione binomiale .

Esempi di distribuzione binomiale

Una volta vista la definizione di distribuzione binomiale, vedremo diversi esempi di variabili che seguono questo tipo di distribuzione per comprendere meglio il concetto.

Numero di volte in cui appare testa lanciando una moneta 25 volte.
Numero di tiri effettuati da un giocatore di basket quando tira verso il canestro 60 volte dalla stessa posizione.
Numero di volte in cui otteniamo il numero 6 lanciando un dado 30 volte.
Numero di superamenti su un totale di 50 studenti che hanno sostenuto un esame.
Numero di unità difettose in un campione di 100 prodotti.

Formula di distribuzione binomiale

Dati i parametri x, n, p, la funzione di probabilità della distribuzione binomiale è definita come il numero combinatorio di n in x volte p ^x volte (1-p) ^nx .

Pertanto, la formula per calcolare la probabilità di una distribuzione binomiale è:

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la probabilità di una variabile che segue la distribuzione binomiale.

D’altra parte, la probabilità cumulativa della distribuzione binomiale viene calcolata sommando le probabilità del numero di casi di successo in questione e tutte le probabilità precedenti. Quindi, la formula per calcolare la probabilità cumulativa di una distribuzione binomiale è:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Esercizio risolto sulla distribuzione binomiale

Lanciamo una moneta 10 volte, qual è la probabilità che esca 6 teste?

La variabile in questo problema segue una distribuzione binomiale perché tutti i lanci sono indipendenti l’uno dall’altro e hanno anche la stessa probabilità di successo.

Concretamente la probabilità di successo è del 50%, poiché solo uno dei due possibili risultati è considerato un successo.

$p=\cfrac{1}{2}=0,5$

Pertanto, la distribuzione per questo esercizio è binomiale con un totale di 10 esperimenti e una probabilità di 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Quindi, per determinare la probabilità che esca sei teste, dobbiamo applicare la formula della distribuzione binomiale.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Quindi, la probabilità di ottenere esattamente sei teste lanciando una moneta dieci volte è del 20,51%.

Caratteristiche della distribuzione binomiale

La distribuzione binomiale ha le seguenti caratteristiche:

La distribuzione binomiale è definita con due parametri: n è il numero totale di esperimenti di Bernoulli e, invece, p è la probabilità di successo di ciascun esperimento di Bernoulli.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

La media di una distribuzione binomiale è uguale al prodotto del numero totale di esperimenti moltiplicato per la probabilità di successo di ciascun esperimento. Pertanto, per calcolare la media di una distribuzione binomiale, bisogna moltiplicare n per p .

$E[X]=n\cdot p$

La varianza di una distribuzione binomiale è uguale al numero totale di prove moltiplicato per la probabilità di successo e la probabilità di fallimento.

$Var(X)=n\cdot p\cdot (1-p)$

La formula per la funzione di probabilità della distribuzione binomiale è la seguente:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Allo stesso modo, la formula per la funzione di distribuzione cumulativa della distribuzione binomiale è:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

La somma di due distribuzioni binomiali indipendenti con la stessa probabilità equivale a una distribuzione binomiale con lo stesso valore di probabilità p e n essendo la somma del numero totale di prove delle due distribuzioni.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

La distribuzione di Bernoulli è un caso speciale di distribuzione binomiale in cui n=1 , cioè viene effettuato un solo esperimento.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Se _X 1 , _X ₂ ,…, X _k sono variabili casuali indipendenti tali che

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

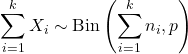
Calcolatore della distribuzione binomiale

Inserisci i valori dei parametri p, n e x della distribuzione binomiale nella seguente calcolatrice per calcolare la probabilità. Devi selezionare la probabilità che vuoi calcolare e inserire i numeri utilizzando il punto come separatore decimale, ad esempio 0,1667.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più