Distribuzione binomiale negativa

Di Benjamin anderson Agosto 3, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è la distribuzione binomiale negativa e a cosa serve. Troverai anche la formula per la distribuzione binomiale negativa, un esempio concreto e le proprietà di questo tipo di distribuzione di probabilità. Infine, potrai calcolare qualsiasi probabilità di distribuzione binomiale negativa con un calcolatore online.

Qual è la distribuzione binomiale negativa?

La distribuzione binomiale negativa è una distribuzione di probabilità che descrive il numero di prove Bernoulliane necessarie per ottenere un dato numero di risultati positivi.

Pertanto, una distribuzione binomiale negativa ha due parametri caratteristici: r è il numero di risultati positivi desiderati e p è la probabilità di successo per ogni esperimento di Bernoulli eseguito.

$X\sim \text{BN}(r,p)$

Ricorda che un test di Bernoulli è un esperimento che ha due possibili esiti: “successo” e “fallimento”. Quindi se la probabilità di “successo” è p , la probabilità di “fallimento” è q=1-p .

Pertanto, una distribuzione binomiale negativa definisce un processo in cui vengono eseguite tutte le prove di Bernoulli necessarie per ottenere risultati positivi. Inoltre, tutti questi studi di Bernoulli sono indipendenti e hanno una probabilità di successo costante.

Ad esempio, una variabile casuale che segue una distribuzione binomiale negativa è il numero di volte in cui è necessario lanciare un dado finché non viene lanciato tre volte il numero 6.

La differenza tra una distribuzione binomiale negativa e una distribuzione binomiale è che la distribuzione binomiale negativa conta il numero di volte necessarie per ottenere un certo numero di risultati positivi, mentre la distribuzione binomiale conta il numero di casi positivi in una serie di test di Bernoulli.

➤ Vedi: Cos’è la distribuzione binomiale?

Formula di distribuzione binomiale negativa

Dati i parametri r, p, x, la probabilità di una distribuzione binomiale negativa viene calcolata moltiplicando il numero combinatorio di x-1 in xr per (1-p) ^xr per p ^r .

Quindi, la formula per calcolare una probabilità di distribuzione binomiale negativa è:

Formula di distribuzione binomiale negativa

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la probabilità di una variabile che segue la distribuzione binomiale negativa.

Esercizio risolto della distribuzione binomiale negativa

Qual è la probabilità che lanciando una moneta otto volte, all’ottavo lancio esca testa una quarta volta?

Per prima cosa dobbiamo calcolare la probabilità che esca testa lanciando una moneta. In questo caso, abbiamo solo un risultato positivo (testa) su due possibili risultati (testa e croce), quindi la probabilità di successo è:

$p=\cfrac{1}{2}=0,5$

Pertanto, la variabile casuale in questo problema segue una distribuzione binomiale negativa dove r=4 e p=0,5. Utilizziamo quindi la formula della distribuzione binomiale negativa per calcolare la probabilità che l’esercizio ci chiede di fare.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

Caratteristiche della distribuzione binomiale negativa

Di seguito sono riportate le caratteristiche più importanti della distribuzione binomiale negativa.

La distribuzione binomiale negativa è definita da due parametri caratteristici: r è il numero di risultati positivi desiderati e p è la probabilità di successo per ogni esperimento di Bernoulli eseguito.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

La varianza di una distribuzione binomiale negativa è uguale a r moltiplicato per (1-p) diviso per p ² .

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

Se il parametro r è maggiore di 1, la modalità di una distribuzione binomiale negativa può essere calcolata con la seguente formula:

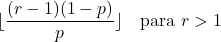
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li> La funzione di massa che permette di determinare una probabilità di distribuzione binomiale negativa è la seguente:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

Il coefficiente di asimmetria di una distribuzione binomiale negativa si calcola con la seguente espressione:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

La curtosi di una distribuzione binomiale negativa può essere trovata con la seguente formula:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

Se il parametro r è uguale a 1, allora abbiamo un caso di distribuzione geometrica .

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Calcolatore della distribuzione binomiale negativa

Inserisci i valori dei parametri r, p, x nella seguente calcolatrice per calcolare la probabilità. È necessario inserire i numeri utilizzando il punto come separatore decimale, ad esempio 0,50.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più