Distribuzione campionaria

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la distribuzione campionaria nelle statistiche e a cosa serve. Troverai quindi il significato di una distribuzione campionaria, un esempio concreto di distribuzione campionaria e, inoltre, le formule per i tipi più comuni di distribuzioni campionarie.

Qual è la distribuzione campionaria?

La distribuzione campionaria , o distribuzione campionaria , è la distribuzione che risulta dalla considerazione di tutti i possibili campioni di una popolazione. In altre parole, la distribuzione campionaria è la distribuzione ottenuta calcolando un parametro di campionamento di tutti i possibili campioni di una popolazione.

Ad esempio, se estraiamo tutti i possibili campioni da una popolazione statistica e calcoliamo la media di ciascun campione, l’insieme delle medie campionarie forma una distribuzione campionaria. Più precisamente, poiché il parametro calcolato è la media aritmetica, si tratta della distribuzione campionaria della media.

In statistica, la distribuzione campionaria viene utilizzata per calcolare la probabilità di avvicinarsi al valore del parametro della popolazione quando si studia un singolo campione. Allo stesso modo, la distribuzione campionaria ci consente di stimare l’errore di campionamento per una data dimensione del campione.

Esempio di distribuzione campionaria

Ora che conosciamo la definizione di distribuzione campionaria, diamo un’occhiata a un semplice esempio per comprendere appieno il concetto.

In una scatola mettiamo tre palline e su ciascuna è scritto un numero da uno a tre, in modo che una pallina abbia il numero 1, un’altra pallina abbia il numero 2 e l’ultima pallina abbia il numero 3. Per un campione di dimensione n = 2, calcola le probabilità della distribuzione campionaria della media se vengono selezionati campioni con sostituzione.

La selezione dei campioni avviene con reinserimento, ovvero la pallina raccolta per selezionare il primo elemento del campione viene rimessa nella scatola e potrà essere nuovamente selezionata durante la seconda estrazione. Pertanto, tutti i possibili campioni della popolazione sono:

1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3

Pertanto, calcoliamo la media aritmetica di ogni possibile campione:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Pertanto, le probabilità di ottenere ciascun valore della media campionaria quando si seleziona un campione casuale dalla popolazione sono le seguenti:

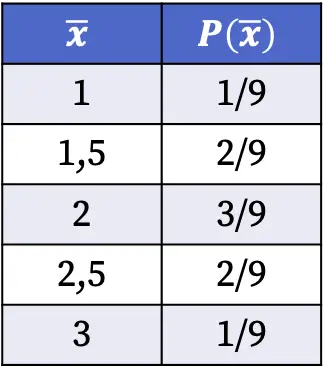
esempio di tabella di distribuzione del campione

Le probabilità della distribuzione campionaria mostrate nella tabella sopra sono state calcolate dividendo il numero di campioni aventi detto valore medio per il numero totale di casi possibili. Ad esempio: la media campionaria è 1,5 in due casi su nove possibili, quindi P(1,5)=2/9.

Tipi di distribuzioni campionarie

Le distribuzioni campionarie (o distribuzioni campionarie) possono essere classificate in base al parametro campionario da cui sono state ottenute. Pertanto, i tipi più comuni di distribuzioni sono i seguenti:

Distribuzione campionaria della media : Questa è la distribuzione campionaria che risulta dal calcolo della media aritmetica di ciascun campione.
Distribuzione campionaria proporzionale : è la distribuzione campionaria ottenuta calcolando la proporzione di tutti i campioni.
Distribuzione campionaria della varianza : Questa è la distribuzione campionaria che forma l’insieme di tutte le varianze nel campione.
Differenza delle medie della distribuzione campionaria : è la distribuzione campionaria che risulta dal calcolo della differenza tra le medie di tutti i possibili campioni provenienti da due popolazioni diverse.
Differenza nelle proporzioni Distribuzione campionaria : è la distribuzione campionaria ottenuta sottraendo tutte le possibili proporzioni campionarie da due popolazioni.

Ciascun tipo di distribuzione campionaria è spiegato più dettagliatamente di seguito.

Distribuzione campionaria della media

Data una popolazione che segue una distribuzione di probabilità normale con media

$\mu$

e deviazione standard

$\sigma$

e vengono estratti campioni di dimensioni

$n$

, la distribuzione campionaria della media sarà definita anche da una distribuzione normale avente le seguenti caratteristiche:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Oro

$\mu_{\overline{x}}$

è la media della distribuzione campionaria della media e

$\sigma_{\overline{x}}$

è la sua deviazione standard. Inoltre,

$\cfrac{\sigma}{\sqrt{n}}$

è l’errore standard della distribuzione campionaria.

Nota: se la popolazione non segue una distribuzione normale ma la dimensione del campione è ampia (n>30), la distribuzione campionaria della media può anche essere approssimata alla distribuzione normale sopra tramite il limite del teorema centrale.

Pertanto, poiché la distribuzione campionaria della media segue una distribuzione normale, la formula per calcolare l’eventuale probabilità relativa alla media campionaria è:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Oro:

$\overline{x}$

è la media del campione.
$\mu$

Questa è la media della popolazione.
$s$

è la deviazione standard della popolazione.
$n$

è la dimensione del campione.
$Z$

è una variabile definita dalla distribuzione normale standard N(0,1).

➤ Vedi: Esercizio risolto sulla distribuzione campionaria della media

Distribuzione campionaria della proporzione

Infatti, quando studiamo una parte di un campione, analizziamo casi di successo. Pertanto, la variabile casuale nello studio segue una distribuzione di probabilità binomiale.

Secondo il teorema del limite centrale, per grandi dimensioni (n>30) possiamo avvicinare una distribuzione binomiale ad una distribuzione normale. Pertanto, la distribuzione campionaria della proporzione approssima una distribuzione normale con i seguenti parametri:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Oro

$p$

è la probabilità di successo e

$q$

è la probabilità di fallimento

$q=1-p$

Nota: una distribuzione binomiale può essere approssimata a una distribuzione normale solo se

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

$nq\ge 5$

Pertanto, poiché la distribuzione campionaria della proporzione può essere approssimata ad una distribuzione normale, la formula per calcolare l’eventuale probabilità relativa alla proporzione di un campione è:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Oro:

$\widehat{p}$

è la proporzione campionaria.
$p$

è la proporzione della popolazione.
$q$

è la probabilità di fallimento della popolazione,

$q=1-p$

.
$n$

è la dimensione del campione.
$Z$

è una variabile definita dalla distribuzione normale standard N(0,1).

➤ Vedi: Esercizio risolto sulla distribuzione campionaria della proporzione

Distribuzione campionaria della varianza

La distribuzione campionaria della varianza è definita dalla distribuzione di probabilità chi-quadrato. Pertanto, la formula per la statistica della distribuzione campionaria della varianza è:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Oro:

$\chi^2$

è la statistica della distribuzione campionaria della varianza, che segue una distribuzione chi-quadrato.
$n$

è la dimensione del campione.
$s^2$

è la varianza campionaria.
$\sigma^2$

è la varianza della popolazione.

➤ Vedi: Esercizio risolto sulla distribuzione campionaria della varianza

Distribuzione campionaria della differenza delle medie

Se la dimensione del campione è sufficientemente grande (n ₁ ≥ 30 e n ₂ ≥ 30), la distribuzione campionaria della differenza media segue una distribuzione normale. Più precisamente, i parametri di detta distribuzione vengono calcolati come segue:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Nota: se entrambe le popolazioni sono distribuzioni normali, la distribuzione campionaria della differenza nelle medie segue una distribuzione normale indipendentemente dalle dimensioni del campione.

Pertanto, poiché la distribuzione campionaria della differenza delle medie è definita da una distribuzione normale, la formula per calcolare la statistica della distribuzione campionaria della differenza delle medie è:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Oro:

$\overline{x_i}$

è la media del campione i.
$\mu_i$

è la media della popolazione i.
$\sigma_i$

è la deviazione standard della popolazione i.
$n_i$

è la dimensione del campione i.
$Z$

è una variabile definita dalla distribuzione normale standard N(0,1).

Si noti che i campioni provenienti da popolazioni diverse possono avere dimensioni campione diverse.

➤ Vedi: Esercizio risolto sulla distribuzione campionaria della differenza delle medie

Distribuzione campionaria delle differenze nelle proporzioni

I campioni selezionati per la differenza nelle proporzioni della distribuzione campionaria sono definiti da distribuzioni binomiali, poiché per scopi pratici una proporzione è un rapporto tra i casi di successo e il numero totale di osservazioni.

Tuttavia, a causa del teorema del limite centrale, le distribuzioni binomiali possono essere approssimate alle normali distribuzioni di probabilità. Pertanto, la distribuzione campionaria della differenza di proporzioni può essere approssimata ad una distribuzione normale con le seguenti caratteristiche:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Nota: la distribuzione campionaria della differenza nelle proporzioni può essere approssimata a una distribuzione normale solo se

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Pertanto, poiché la distribuzione campionaria della differenza di proporzioni può essere approssimata ad una distribuzione normale, la formula per calcolare la statistica della distribuzione campionaria della differenza di proporzioni è la seguente:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Oro:

$\widehat{p_i}$

è la proporzione campionaria i.
$p_i$

è la proporzione della popolazione i.
$q_i$

è la probabilità di fallimento della popolazione i,

$q_i=1-p_i$

.
$n_i$

è la dimensione del campione i.
$Z$

è una variabile definita dalla distribuzione normale standard N(0,1).

➤ Vedi: Esercizio risolto sulla distribuzione campionaria della differenza di proporzioni

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Qual è la distribuzione campionaria?

Esempio di distribuzione campionaria

Tipi di distribuzioni campionarie

Distribuzione campionaria della media

Distribuzione campionaria della proporzione

Distribuzione campionaria della varianza

Distribuzione campionaria della differenza delle medie

Distribuzione campionaria delle differenze nelle proporzioni

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento