Distribuzione campionaria della differenza delle medie

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega qual è la distribuzione campionaria della differenza tra due medie nelle statistiche. Troverai anche la formula per la distribuzione campionaria della differenza delle medie e, inoltre, un esercizio risolto passo passo.

Qual è la distribuzione campionaria della differenza delle medie?

La distribuzione campionaria della differenza nelle medie è la distribuzione che risulta dal calcolo delle differenze tra le medie di tutti i possibili campioni di due popolazioni diverse.

Cioè, per ottenere la distribuzione campionaria della differenza nelle medie, è necessario selezionare tutti i possibili campioni di due popolazioni di studio, quindi calcolare la media di ciascun campione selezionato e, infine, calcolare la differenza tra tutte le medie delle due popolazioni. Pertanto, l’insieme dei valori ottenuti dopo l’applicazione di tutte queste operazioni costituisce la distribuzione campionaria della differenza delle medie.

distribuzione campionaria della differenza delle medie

La differenza delle medie della distribuzione campionaria viene utilizzata per calcolare la probabilità che la differenza tra due medie di campioni selezionati casualmente da due popolazioni diverse sia vicina alla differenza nelle medie della popolazione.

➤ Vedi: Distribuzione campionaria della media

Formula per la distribuzione campionaria della differenza delle medie

Se la dimensione del campione è sufficientemente grande (n ₁ ≥ 30 e n ₂ ≥ 30), la distribuzione campionaria della differenza nelle medie segue una distribuzione normale. Più precisamente, i parametri di detta distribuzione vengono calcolati come segue:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Nota: se entrambe le popolazioni sono distribuzioni normali , la distribuzione campionaria della differenza nelle medie segue una distribuzione normale indipendentemente dalle dimensioni del campione.

Pertanto, poiché la distribuzione campionaria della differenza delle medie è definita da una distribuzione normale, la formula per calcolare la statistica della distribuzione campionaria della differenza delle medie è:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Oro:

$\overline{x_i}$

è la media del campione i.
$\mu_i$

è la media della popolazione i.
$\sigma_i$

è la deviazione standard della popolazione i.
$n_i$

è la dimensione del campione i.
$Z$

è una variabile definita dalla distribuzione normale standard N(0,1).

Si noti che i campioni provenienti da popolazioni diverse possono avere dimensioni campione diverse.

Esempio concreto di distribuzione campionaria della differenza delle medie

Una volta vista la definizione di differenza della distribuzione campionaria delle medie e qual è la sua formula, vedremo un esempio passo passo per completare la comprensione del concetto di differenza della distribuzione campionaria delle medie.

In uno studio statistico vogliamo analizzare la differenza tra l’altezza dei ragazzi e delle ragazze di una certa età. Sappiamo che la distribuzione che definisce la popolazione dei ragazzi di questa età ha una media di 157 cm e una deviazione standard di 9 cm e, invece, la distribuzione che definisce la popolazione delle ragazze di questa età ha una media di 148 cm e una deviazione standard di 7 cm. Se si seleziona un campione di 30 ragazzi di questa età e un campione di 35 ragazze di questa età, qual è la probabilità che l’altezza media del campione di ragazzi sia di 12 cm maggiore dell’altezza media del campione di ragazze?

Per risolvere questo problema, la prima cosa da fare è calcolare la statistica della distribuzione campionaria della differenza delle medie. Applichiamo quindi la formula vista sopra:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

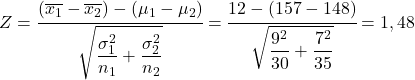
Pertanto, la probabilità che l’altezza media del campione dei ragazzi sia di 12 cm maggiore dell’altezza media delle ragazze è equivalente alla probabilità che la variabile Z sia maggiore di 1,48.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p> </p> <p> Cerchiamo quindi la probabilità di Z>1,48 nella <a href=$ tabella di Z :

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p> </p> <p> In breve, la probabilità che l’altezza media del campione dei ragazzi sia di 12 cm maggiore dell’altezza media delle ragazze è del 6,94%.</p> </div>  <div class=$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Qual è la distribuzione campionaria della differenza delle medie?

Formula per la distribuzione campionaria della differenza delle medie

Esempio concreto di distribuzione campionaria della differenza delle medie

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento