Distribuzione campionaria delle differenze nelle proporzioni
Questo articolo spiega qual è la differenza nella distribuzione del campionamento proporzionale e a cosa serve nelle statistiche. Vengono inoltre presentati la differenza nella formula di distribuzione del campionamento delle proporzioni e un esercizio risolto passo dopo passo.
Qual è la distribuzione campionaria della differenza nelle proporzioni?
La differenza nelle proporzioni della distribuzione di campionamento è la distribuzione che risulta dal calcolo delle differenze tra le proporzioni di campionamento di tutti i possibili campioni di due popolazioni diverse.
Cioè, il processo per ottenere la distribuzione campionaria della differenza nelle proporzioni consiste, in primo luogo, nell’estrarre tutti i possibili campioni da due popolazioni diverse, in secondo luogo, nel determinare la proporzione di ciascun campione estratto e, infine, nel determinare la differenza tra tutti i proporzioni della differenza di proporzioni. due popolazioni. In modo che l’insieme dei risultati ottenuti dopo aver eseguito queste operazioni costituisce la distribuzione campionaria della differenza di proporzioni.

In statistica, la differenza nelle proporzioni della distribuzione campionaria viene utilizzata per calcolare la probabilità che la differenza tra le proporzioni campionarie di due campioni selezionati casualmente sia vicina alla differenza nelle proporzioni della popolazione.
Formula per la distribuzione campionaria della differenza di proporzioni
I campioni selezionati per la differenza nelle proporzioni della distribuzione campionaria sono definiti da distribuzioni binomiali , perché per scopi pratici, una proporzione è un rapporto tra i casi riusciti e il numero totale di osservazioni.
Tuttavia, a causa del teorema del limite centrale, le distribuzioni binomiali possono essere approssimate alle normali distribuzioni di probabilità . Pertanto, la distribuzione campionaria della differenza di proporzioni può essere approssimata ad una distribuzione normale con le seguenti caratteristiche:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
Nota: la distribuzione campionaria della differenza nelle proporzioni può essere approssimata a una distribuzione normale solo se
![]()
,
![]()
,
![]()
,
![]()
,
![]()
E
![]()
.
Pertanto, poiché la distribuzione campionaria della differenza di proporzioni può essere approssimata ad una distribuzione normale, la formula per calcolare la statistica della distribuzione campionaria della differenza di proporzioni è la seguente:

Oro:
-

è la proporzione campionaria i.
-

è la proporzione della popolazione i.
-

è la probabilità di fallimento della popolazione i,

.
-

è la dimensione del campione i.
-

è una variabile definita dalla distribuzione normale standard N(0,1).
Questa formula è simile alla formula di verifica dell’ipotesi per la differenza nelle proporzioni.
Esempio concreto di distribuzione campionaria di differenza di proporzioni
Dopo aver visto la definizione di distribuzione campionaria della differenza di proporzioni e qual è la sua formula, puoi vedere di seguito un esempio risolto passo dopo passo per completare la comprensione del concetto.
- Si desidera analizzare la precisione di due impianti di produzione, uno stabilimento produce in modo tale che solo il 5% delle parti prodotte presenta difetti, mentre la percentuale di parti difettose di un’altra fabbrica è dell’8%. Se prendiamo un campione di 200 pezzi dal primo stabilimento e un altro campione di 280 pezzi dal secondo stabilimento, qual è la probabilità che la percentuale di difetti nel primo impianto di produzione sia maggiore della percentuale di difetti nel secondo stabilimento? produzione?
Per finire di conoscere tutti i dati del problema, calcoleremo prima la proporzione delle parti ben prodotte di ciascuna pianta:
![Rendered by QuickLaTeX.com \begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7c02732cc5fb319bfa5bf7b8ed8d03db_l3.png)
Se il tasso di difetti nella prima fabbrica fosse maggiore del tasso di difetti nella seconda fabbrica, ciò significa che sarebbe vera la seguente equazione:
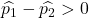
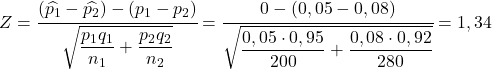
Pertanto, la probabilità che il tasso di difetti della prima fabbrica sia maggiore del tasso di difetti della seconda fabbrica è equivalente alla probabilità che la variabile Z sia maggiore di 1,34:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”></p>
</p>
<p> Infine, non ci resta che cercare la probabilità corrispondente nella <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-41dd897cdff473ff488cde0e3cc140b0_l3.png) tabella della distribuzione normale e avremo già risolto il problema:
tabella della distribuzione normale e avremo già risolto il problema:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”></p>
</p>
<p> In breve, la probabilità che la percentuale di difetti nella prima fabbrica sia maggiore della proporzione di difetti nella seconda fabbrica è del 9,01%. </p>
<div style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d6e503a2089d30be8fd68bbc722bb44_l3.png) ➤ Vedi: Distribuzione campionaria della differenza nelle medie
➤ Vedi: Distribuzione campionaria della differenza nelle medie