Distribuzione campionaria della media
Questo articolo spiega qual è la distribuzione campionaria della media nelle statistiche. Troverai anche la formula della distribuzione media campionaria e un esercizio risolto passo dopo passo.
Qual è la distribuzione campionaria della media?
La distribuzione campionaria della media (o distribuzione campionaria delle medie ) è la distribuzione che risulta dal calcolo della media campionaria di ogni possibile campione di una popolazione. Cioè, l’insieme delle medie campionarie di tutti i possibili campioni di una popolazione costituisce la distribuzione campionaria della media.
O in altre parole, se studiamo tutti i campioni prelevabili da una popolazione e calcoliamo la media di ciascuno dei campioni, l’insieme dei valori calcolati forma una distribuzione campionaria della media campionaria.
In statistica, la distribuzione campionaria della media viene utilizzata per calcolare la probabilità di avvicinarsi al valore della media della popolazione quando si analizza un singolo campione.
Formula per la distribuzione campionaria della media
Data una popolazione che segue una distribuzione di probabilità normale con media
![]()
e deviazione standard
![]()
e vengono estratti campioni di dimensioni
![]()
, la distribuzione campionaria della media sarà definita anche da una distribuzione normale avente le seguenti caratteristiche:
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
Oro
![]()
è la media della distribuzione campionaria della media e
![]()
è la sua deviazione standard. Inoltre,
![]()
è l’errore standard della distribuzione campionaria.
Nota: se la popolazione non segue una distribuzione normale ma la dimensione del campione è ampia (n>30), la distribuzione campionaria della media può anche essere approssimata alla distribuzione normale precedente mediante il teorema del limite centrale.
Pertanto, poiché la distribuzione campionaria della media segue una distribuzione normale, la formula per calcolare l’eventuale probabilità relativa alla media campionaria è:

Oro:
-

è la media del campione.
-

Questa è la media della popolazione.
-

è la deviazione standard della popolazione.
-

è la dimensione del campione.
-

è una variabile definita dalla distribuzione normale standard N(0,1).
Esempio reale della distribuzione campionaria della media
Dopo aver visto la definizione di distribuzione campionaria della media e quali sono le formule ad essa associate, risolviamo un esempio per comprendere meglio il concetto.
- Il peso degli studenti universitari segue una distribuzione normale con una media di 68 kg e una deviazione standard di 9 kg. Determinato:
- Qual è la probabilità che la media di un campione casuale di 25 studenti sia inferiore a 66 kg?
- Se si prelevano 300 campioni con una dimensione di 25 studenti ciascuno, quante medie di campioni avranno un valore inferiore a 66 kg?
Prima di tutto dobbiamo calcolare il valore della statistica corrispondente, per questo applichiamo la formula che abbiamo visto sopra:
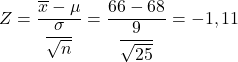
La probabilità che cerchiamo è quindi quella corrispondente al valore Z=-1.11 della coda sinistra della distribuzione normale standard, facilmente ricavabile dalla tabella delle probabilità Z. Utilizziamo quindi la tabella Z per determinare la probabilità che il problema ci chieda:
![]()
Ora che conosciamo la probabilità che la media di un campione casuale sia inferiore a 66 kg, per conoscere la media del numero di campioni inferiore a 66 kg prendendo 300 campioni uguali, dobbiamo moltiplicare la probabilità calcolata per il numero totale di campioni prelevati:
![]()
Pertanto, circa 40 dei campioni estratti avranno un peso medio inferiore a 66 kg.