Come calcolare le distribuzioni campionarie in excel

Una distribuzione campionaria è una distribuzione di probabilità di una certa statistica basata su molti campioni casuali di una singola popolazione .

Questo tutorial spiega come eseguire le seguenti operazioni con le distribuzioni di campionamento in Excel:

• Generare una distribuzione campionaria.
• Visualizzare la distribuzione campionaria.
• Calcolare la media e la deviazione standard della distribuzione campionaria.
• Calcolare le probabilità relative alla distribuzione campionaria.

Generare una distribuzione campionaria in Excel

Supponiamo di voler generare una distribuzione campionaria composta da 1.000 campioni in cui ciascuna dimensione campionaria è 20 e proviene da una distribuzione normale con una media di 5,3 e una deviazione standard di 9 .

Possiamo farlo facilmente digitando la seguente formula nella cella A2 del nostro foglio di calcolo:

 = NORM . INV ( RAND (), 5.3, 9)

Possiamo quindi passare con il mouse sull’angolo in basso a destra della cella finché non appare un piccolo + e trascinare la formula verso destra di 20 celle e verso il basso di 1000 celle:

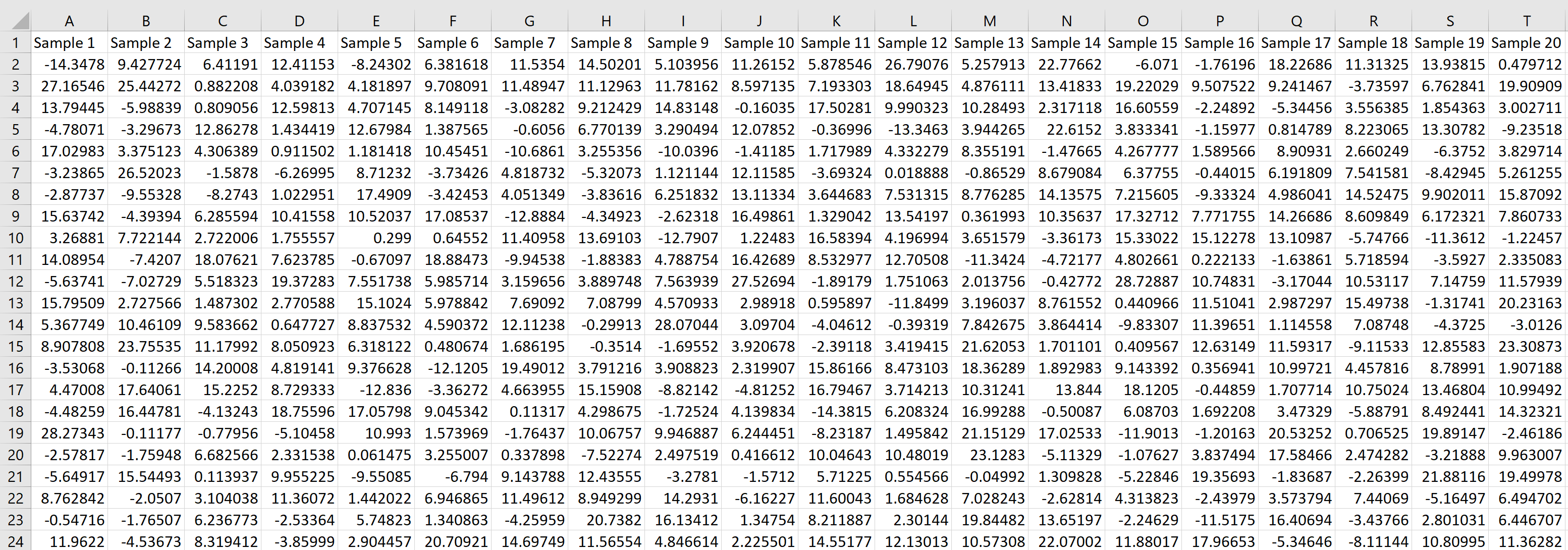
Ogni riga rappresenta un campione di dimensione 20 in cui ciascun valore proviene da una distribuzione normale con una media di 5,3 e una deviazione standard di 9.

Trova la media e la deviazione standard

Per trovare la media e la deviazione standard di questa distribuzione campionaria delle medie campionarie, possiamo prima trovare la media di ciascun campione digitando la seguente formula nella cella U2 del nostro foglio di lavoro:

 = AVERAGE (A2:T2)

Possiamo quindi passare il mouse sull’angolo in basso a destra della cella finché non appare un piccolo + e fare doppio clic per copiare questa formula in tutte le altre celle nella colonna U:

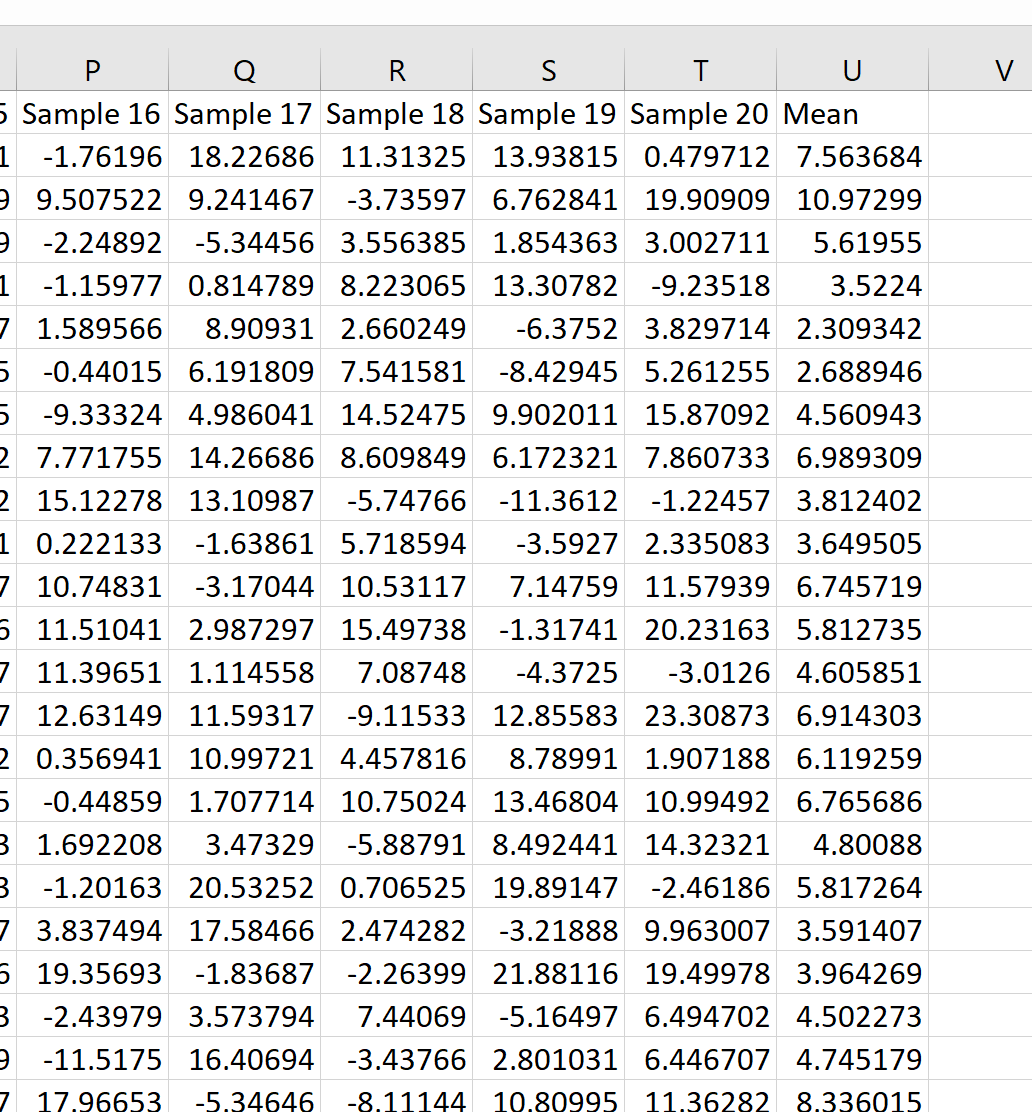
Possiamo vedere che il primo campione aveva una media di 7,563684, il secondo campione aveva una media di 10,97299 e così via.

Possiamo quindi utilizzare le seguenti formule per calcolare la media e la deviazione standard delle medie campionarie:

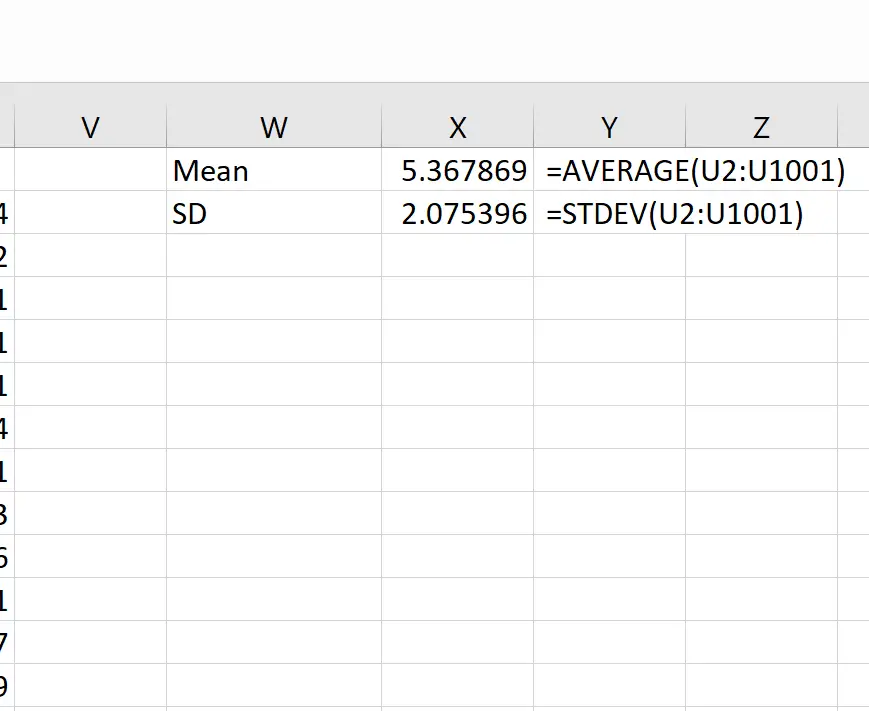
Teoricamente, la media della distribuzione campionaria dovrebbe essere 5,3. Possiamo vedere che la media campionaria effettiva in questo esempio è 5.367869 , che è vicina a 5.3.

E teoricamente, la deviazione standard della distribuzione campionaria dovrebbe essere uguale a s/√n, che sarebbe 9 / √20 = 2,012. Possiamo vedere che la deviazione standard effettiva della distribuzione campionaria è 2.075396 , che è vicina a 2.012.

Visualizzare la distribuzione campionaria

Possiamo anche creare un semplice istogramma per visualizzare la distribuzione campionaria delle medie campionarie.

Per fare ciò, evidenzia semplicemente tutte le medie campione nella colonna U, fai clic sulla scheda Inserisci , quindi fai clic sull’opzione Istogramma nella sezione Grafici .

Ciò fornisce il seguente istogramma:

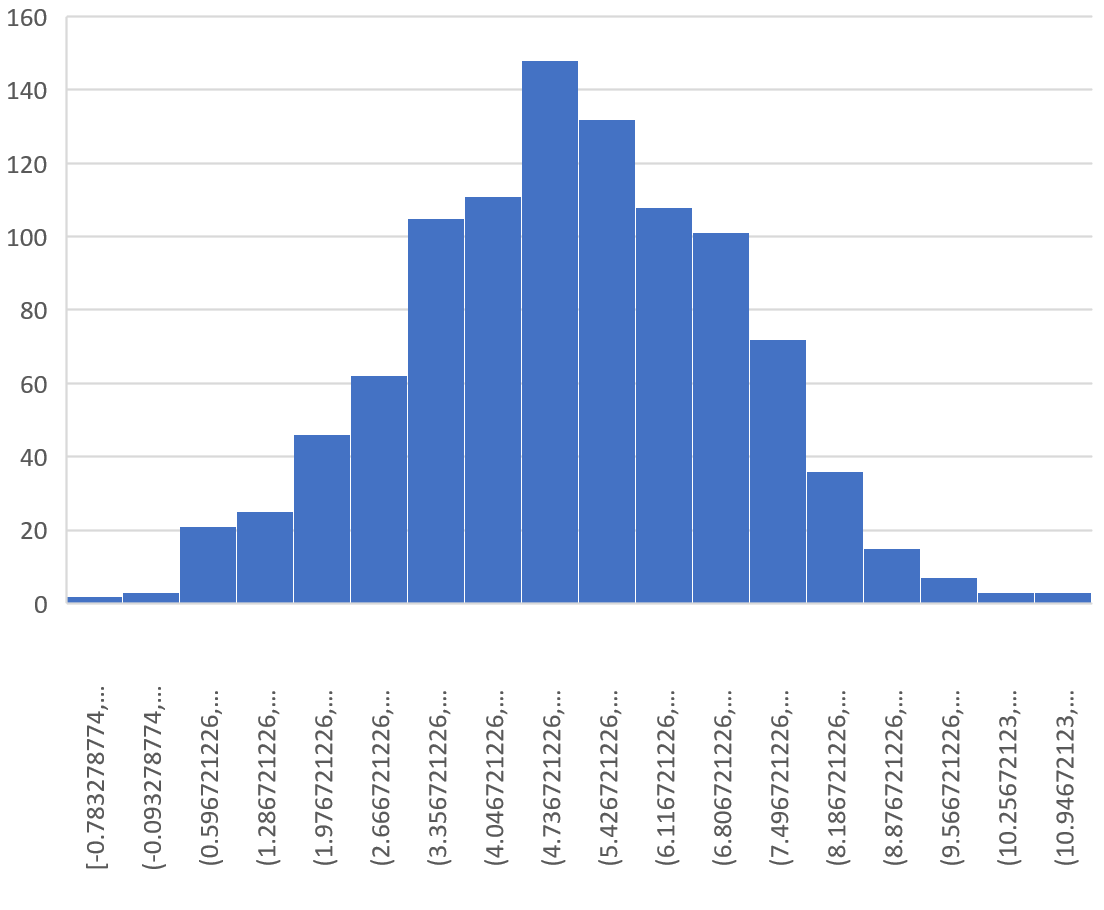
Si può notare che la distribuzione campionaria è a campana con un picco vicino al valore 5.

Tuttavia, dalle code della distribuzione possiamo vedere che alcuni campioni avevano medie maggiori di 10 e altri avevano medie minori di 0.

Calcolare le probabilità

Possiamo anche calcolare la probabilità di ottenere un determinato valore per una media campionaria, in base alla media della popolazione, alla deviazione standard della popolazione e alla dimensione del campione.

Ad esempio, possiamo utilizzare la seguente formula per trovare la probabilità che la media del campione sia inferiore o uguale a 6, dato che la media della popolazione è 5,3, la deviazione standard della popolazione è 9 e la dimensione del campione è:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

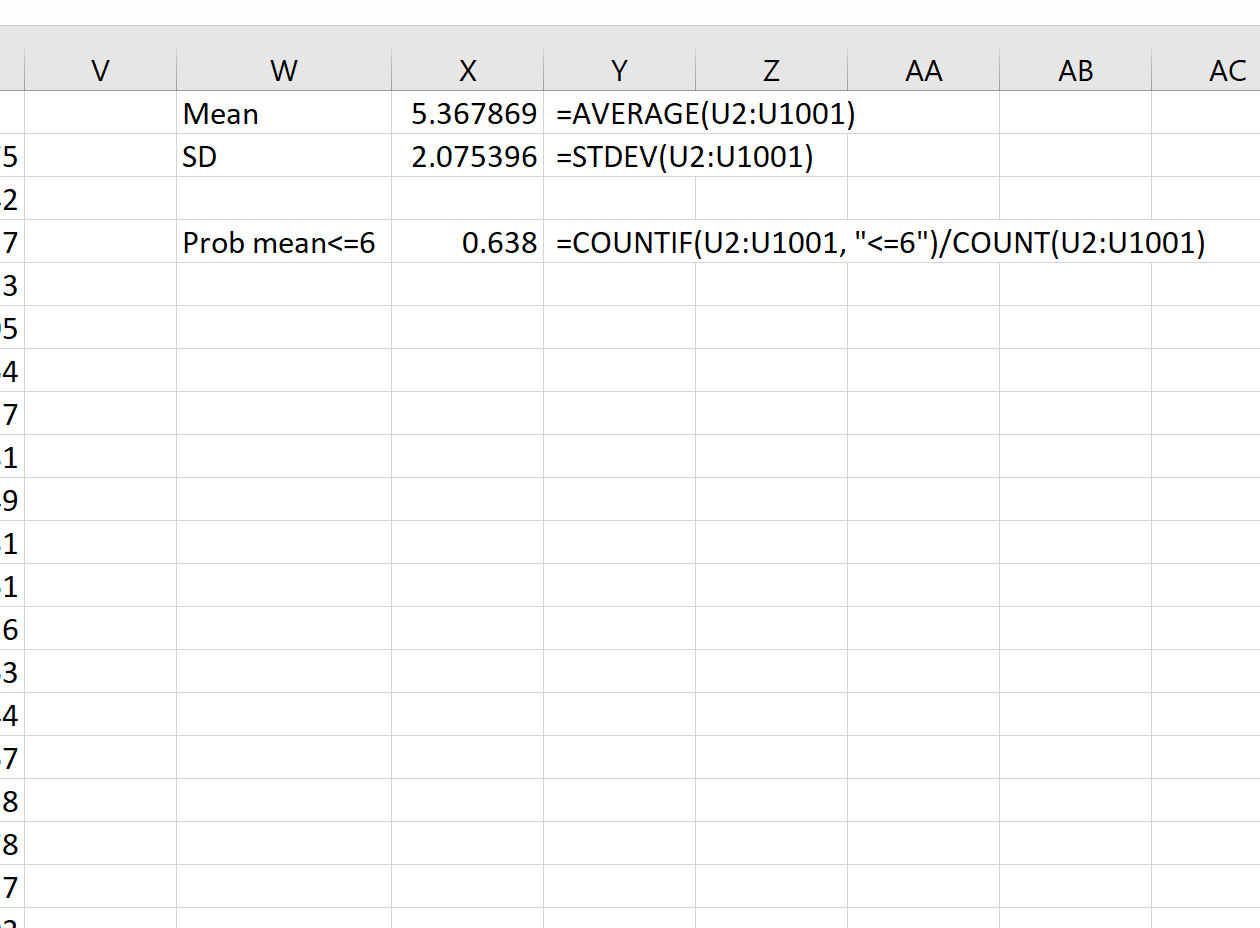
Vediamo che la probabilità che la media campionaria sia inferiore o uguale a 6 è 0,638.

Questo è molto vicino alla probabilità calcolata dal calcolatore della distribuzione campionaria :

Risorse addizionali

Un’introduzione alle distribuzioni campionarie
Calcolatore della distribuzione campionaria
Un’introduzione al teorema del limite centrale