Come calcolare le distribuzioni campionarie in r

Una distribuzione campionaria è una distribuzione di probabilità di una determinata statistica basata su molti campioni casuali di una singola popolazione.

Questo tutorial spiega come eseguire le seguenti operazioni con le distribuzioni di campionamento in R:

• Generare una distribuzione campionaria.
• Visualizzare la distribuzione campionaria.
• Calcolare la media e la deviazione standard della distribuzione campionaria.
• Calcolare le probabilità relative alla distribuzione campionaria.

Generare una distribuzione campionaria in R

Il codice seguente mostra come generare una distribuzione campionaria in R:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

In questo esempio, abbiamo utilizzato la funzione rnorm() per calcolare la media di 10.000 campioni in cui ciascuna dimensione del campione era 20 ed è stata generata da una distribuzione normale con una media di 5,3 e una deviazione standard di 9.

Possiamo vedere che il primo campione aveva una media di 5,283992, il secondo campione aveva una media di 6,304845 e così via.

Visualizzare la distribuzione campionaria

Il codice seguente mostra come creare un semplice istogramma per visualizzare la distribuzione del campionamento:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

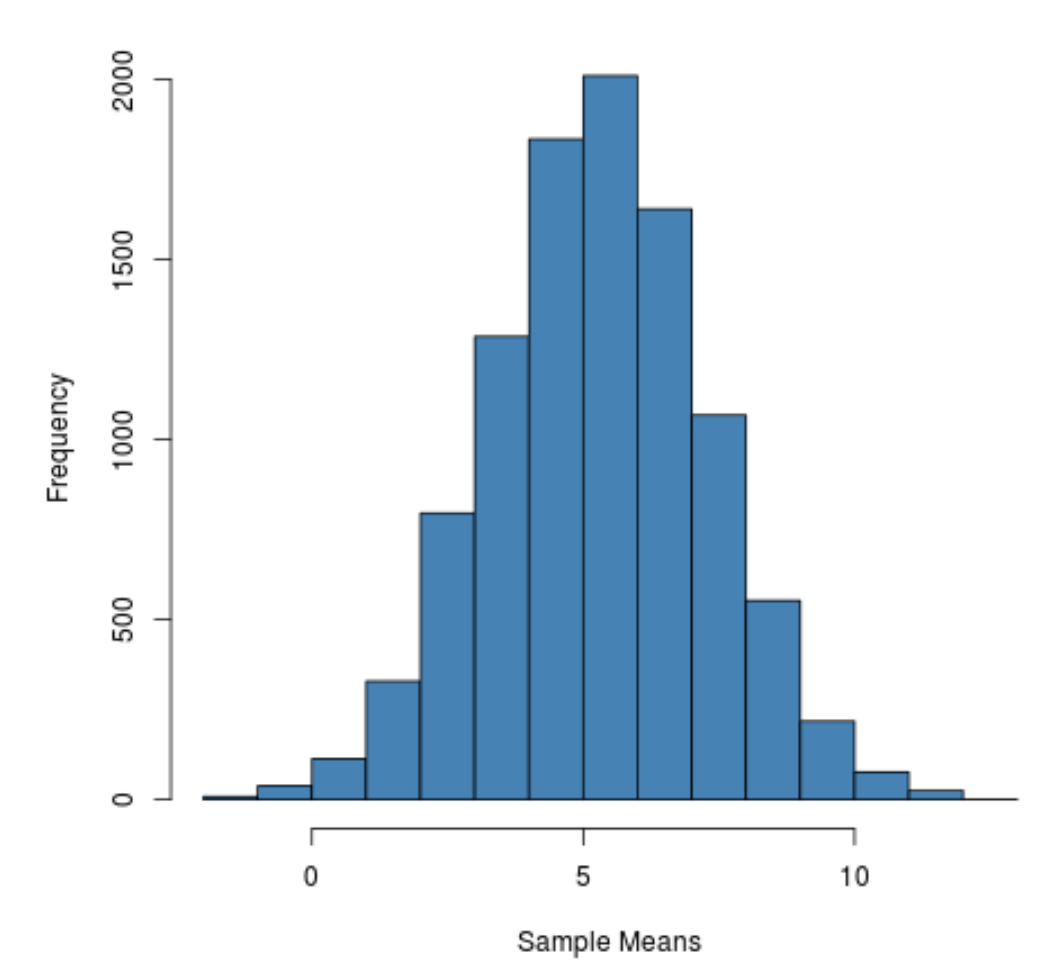
Si può notare che la distribuzione campionaria è a campana con un picco vicino al valore 5.

Tuttavia, dalle code della distribuzione possiamo vedere che alcuni campioni avevano medie maggiori di 10 e altri avevano medie inferiori a 0.

Trova la media e la deviazione standard

Il codice seguente mostra come calcolare la media e la deviazione standard della distribuzione campionaria:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

Teoricamente, la media della distribuzione campionaria dovrebbe essere 5,3. Possiamo vedere che la media campionaria effettiva in questo esempio è 5.287195 , che è vicina a 5.3.

E teoricamente, la deviazione standard della distribuzione campionaria dovrebbe essere uguale a s/√n, che sarebbe 9 / √20 = 2,012. Possiamo vedere che la deviazione standard effettiva della distribuzione campionaria è 2.00224 , che è vicina a 2.012.

Calcolare le probabilità

Il codice seguente mostra come calcolare la probabilità di ottenere un determinato valore per una media campionaria, data la media della popolazione, la deviazione standard della popolazione e la dimensione del campione.

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

In questo esempio particolare, troviamo la probabilità che la media del campione sia inferiore o uguale a 6, dato che la media della popolazione è 5,3, la deviazione standard della popolazione è 9 e la dimensione del campione di 20 è 0,6417 .

Questo è molto vicino alla probabilità calcolata dal calcolatore della distribuzione campionaria :

Il codice completo

Il codice R completo utilizzato in questo esempio è mostrato di seguito:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Risorse addizionali

Un’introduzione alle distribuzioni campionarie
Calcolatore della distribuzione campionaria
Un’introduzione al teorema del limite centrale