Cos'è una distribuzione categorica?

Una distribuzione categoriale è una distribuzione di probabilità discreta che descrive la probabilità che una variabile casuale assuma un valore appartenente a una delle K categorie, dove ciascuna categoria è associata a una probabilità.

Affinché una distribuzione possa essere classificata come distribuzione categoriale, deve soddisfare i seguenti criteri:

• Le categorie sono discrete.
• Esistono due o più categorie potenziali.
• La probabilità che la variabile casuale assuma un valore in ciascuna categoria deve essere compresa tra 0 e 1.
• La somma delle probabilità per tutte le categorie deve essere pari a 1.

L’esempio più ovvio di distribuzione categoriale è la distribuzione dei risultati associati al lancio di un dado. Ci sono K = 6 risultati potenziali e la probabilità di ciascun risultato è 1/6:

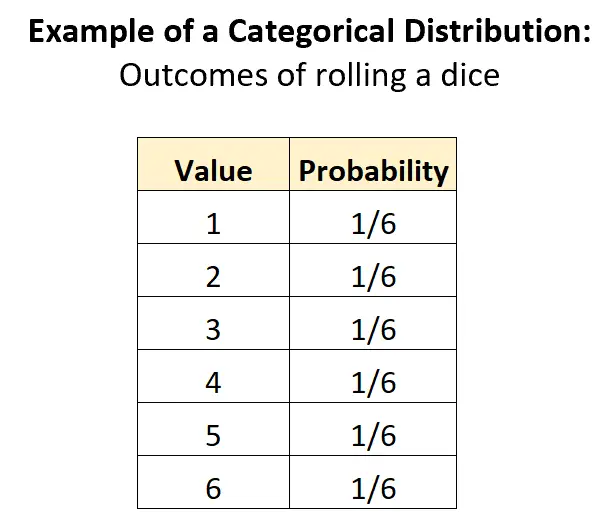
Questa distribuzione soddisfa tutti i criteri per essere classificata come distribuzione categoriale:

• Le categorie sono discrete (ad esempio la variabile casuale può assumere solo valori discreti – 1, 2, 3, 4, 5, 6)
• Esistono due o più categorie potenziali.
• La probabilità di ciascuna categoria è compresa tra 0 e 1.
• La somma delle probabilità è 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Regola generale:

Se riesci a contare il numero di risultati, allora stai lavorando con una variabile casuale discreta, ad esempio contando il numero di volte in cui una moneta esce testa.

Ma se puoi misurare il risultato, stai lavorando con una variabile casuale continua, ad esempio misurando altezza, peso, tempo, ecc.

Altri esempi di distribuzioni categoriali

Esistono molte distribuzioni categoriche nel mondo reale, tra cui:

Esempio 1: lancia una moneta.

Quando lanciamo una moneta, ci sono 2 potenziali risultati discreti, la probabilità di ciascun risultato è compresa tra 0 e 1 e la somma delle probabilità è uguale a 1:

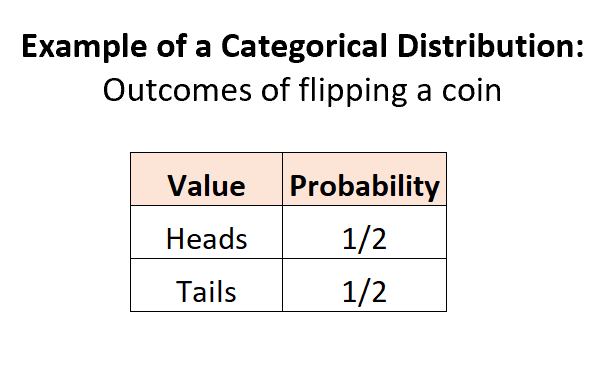
Esempio 2: Selezione delle biglie in un’urna.

Supponiamo che un’urna contenga 5 biglie rosse, 3 biglie verdi e 2 biglie viola. Se selezioniamo casualmente una pallina dall’urna, ci sono 3 potenziali risultati discreti, la probabilità di ciascun risultato è compresa tra 0 e 1 e la somma delle probabilità è uguale a 1:

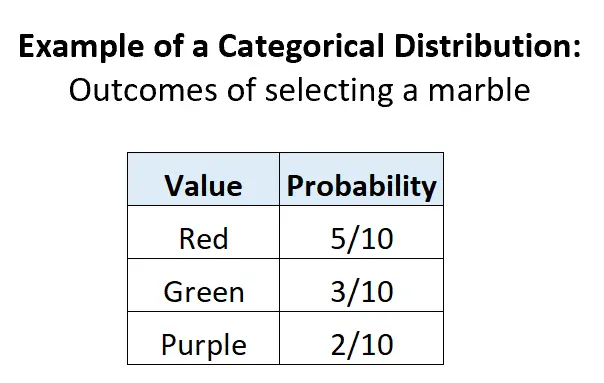
Esempio 3: Selezionare una carta da un mazzo.

Se selezioniamo casualmente una carta da un mazzo standard di 52 carte, ci sono 13 potenziali risultati discreti, la probabilità di ciascun risultato è compresa tra 0 e 1 e la somma delle probabilità è uguale a 1:

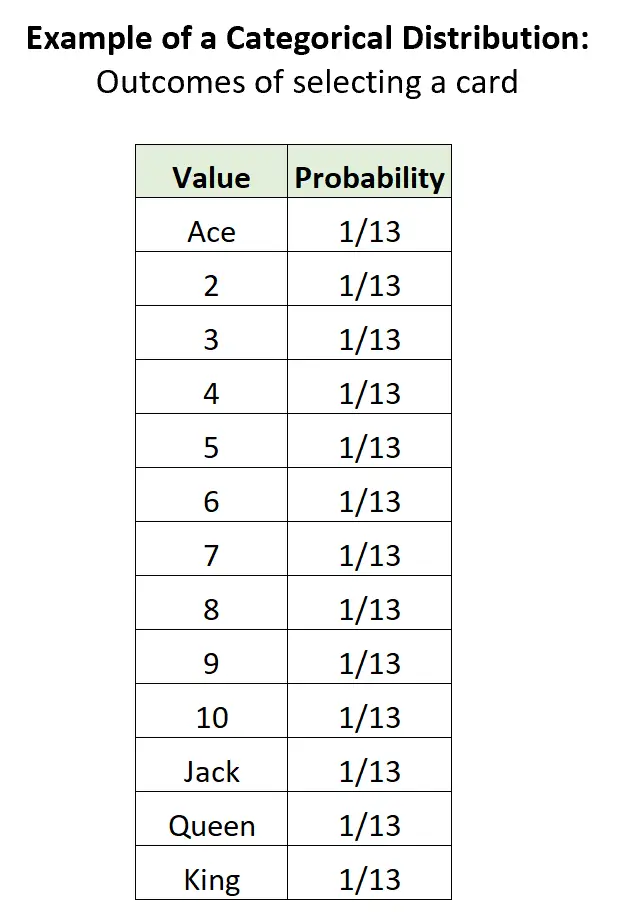
Rapporti con altre distribuzioni

Affinché una distribuzione sia classificata come distribuzione categoriale , deve avere K ≥ 2 risultati potenziali e n = 1 prova.

Utilizzando questa terminologia, una distribuzione categorica è simile alle seguenti distribuzioni:

Distribuzione di Bernoulli: K = 2 risultati, n = 1 test

Distribuzione binomiale: K = 2 endpoint, n ≥ 1 studio

Distribuzione multinomiale: K ≥ 2 risultati, n ≥ prove

Risorse addizionali

Cosa sono le variabili casuali?
Un’introduzione alla distribuzione binomiale
Un’introduzione alla distribuzione multinomiale