Distribuzione chi-quadrato

Di Benjamin anderson Agosto 4, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è la distribuzione chi quadrato e a cosa serve. Inoltre, troverai il grafico della distribuzione chi-quadrato e le sue proprietà.

Qual è la distribuzione chi quadrato?

La distribuzione Chi-quadrato è una distribuzione di probabilità il cui simbolo è χ². Più precisamente, la distribuzione Chi-quadrato è la somma dei quadrati di k variabili casuali indipendenti con distribuzione normale.

Pertanto, la distribuzione Chi-quadrato ha k gradi di libertà. Pertanto, una distribuzione Chi-quadrato ha tanti gradi di libertà quanti sono la somma dei quadrati delle variabili normalmente distribuite che rappresenta.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

La distribuzione Chi-quadrato è anche conosciuta come distribuzione Pearson .

Va notato che la distribuzione Chi-quadrato è un caso speciale della distribuzione gamma.

La distribuzione chi-quadrato è ampiamente utilizzata nell’inferenza statistica, ad esempio nei test di ipotesi e negli intervalli di confidenza. Vedremo di seguito quali sono le applicazioni di questo tipo di distribuzione di probabilità.

Grafico della distribuzione chi-quadrato

Una volta vista la definizione della distribuzione Chi-quadrato, vedremo rappresentati graficamente diversi esempi di questo tipo di distribuzione. Quindi di seguito puoi vedere come il grafico delle probabilità della distribuzione chi-quadrato varia a seconda dei gradi di libertà.

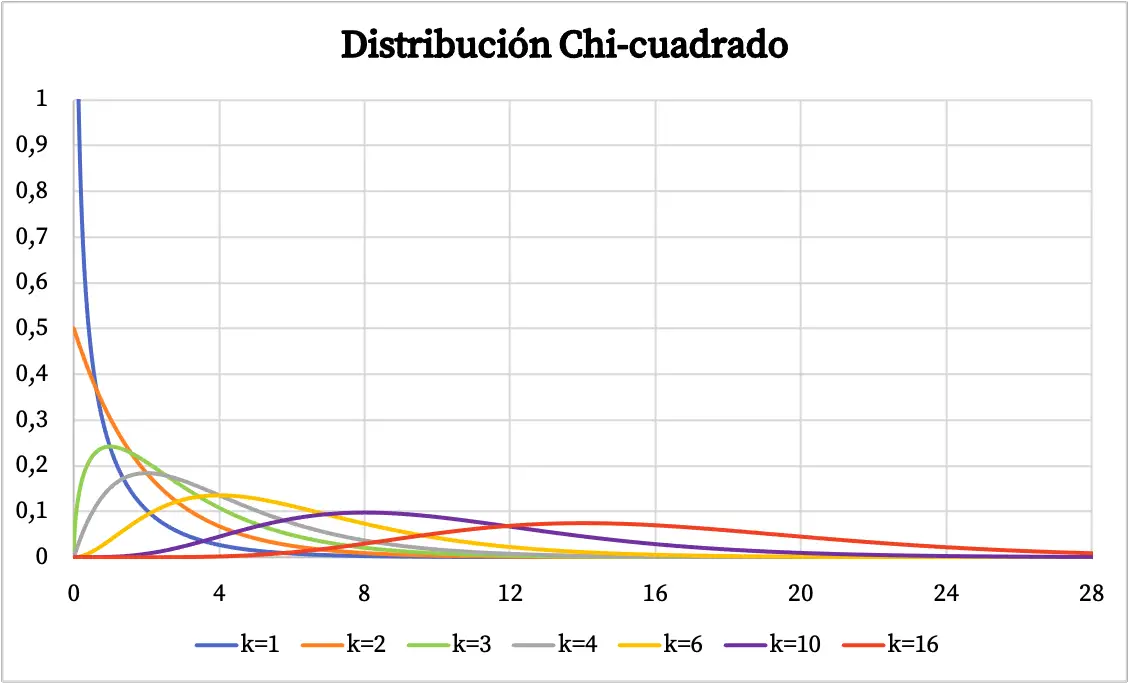
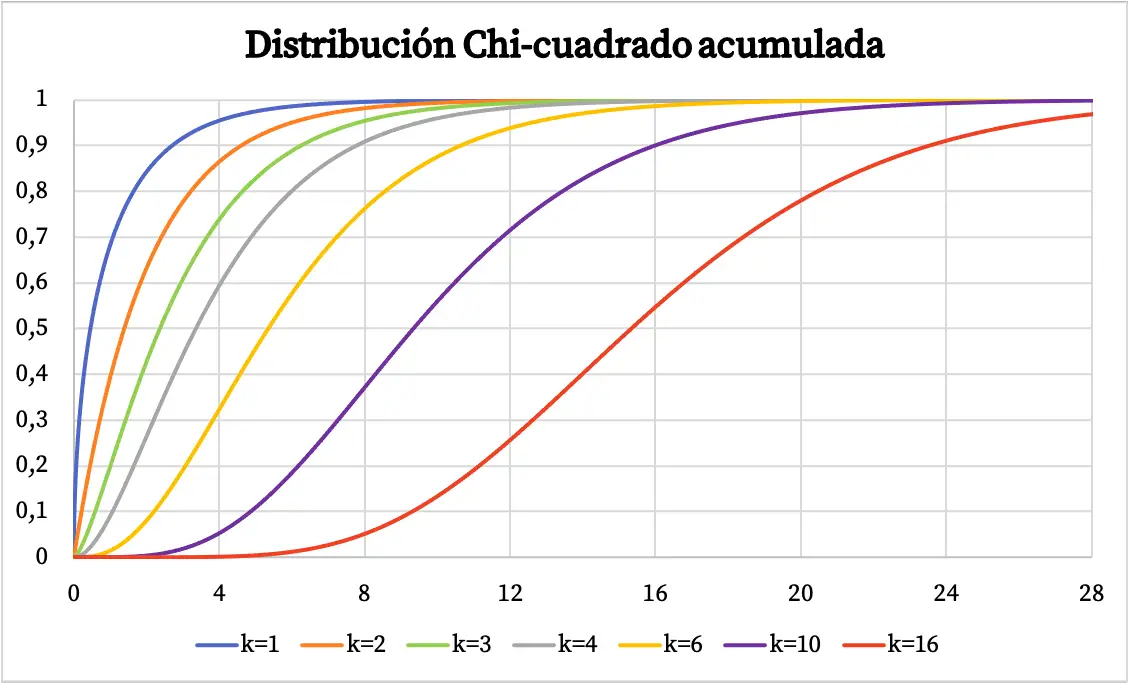
La funzione di densità della distribuzione Chi-quadrato è stata rappresentata nel grafico sopra. D’altra parte, il grafico della funzione di distribuzione della probabilità cumulativa chi-quadrato è il seguente:

grafico della distribuzione cumulativa chi-quadrato

➤ Vedi: tabella della distribuzione del chi-quadrato

Caratteristiche della distribuzione chi-quadrato

In questa sezione vedremo le proprietà più importanti della distribuzione Chi-quadrato legate alla teoria e alla statistica della probabilità.

La media di una distribuzione chi-quadrato è uguale ai suoi gradi di libertà.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

La varianza di una distribuzione Chi-quadrato è pari al doppio dei gradi di libertà della distribuzione.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

La modalità di una distribuzione chi-quadrato è due unità in meno dei suoi gradi di libertà, purché la distribuzione abbia più di un grado di libertà.

$Mo=k-2 \qquad \text{si } k\geq 2$

La funzione di densità della distribuzione Chi-quadrato è zero se x=0. Tuttavia, per valori di x maggiori di 0, la funzione di densità di una distribuzione Chi-quadrato è definita dalla seguente formula:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

La funzione di distribuzione cumulativa della distribuzione Chi-quadrato è governata dalla seguente formula:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

Il coefficiente di asimmetria della distribuzione Chi-quadrato è la radice quadrata del quoziente di otto divisa per il numero di gradi di libertà della distribuzione.

$\displaystyle A=\sqrt{\frac{8}{k}}$

La curtosi della distribuzione Chi-quadrato viene calcolata utilizzando la seguente espressione:

$C=3+\cfrac{12}{k}$

A causa del teorema del limite centrale, la distribuzione chi quadrato può essere approssimata da una distribuzione normale se k è sufficientemente grande.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

Applicazioni della distribuzione chi-quadrato

La distribuzione chi-quadrato ha molte applicazioni diverse in statistica. Esiste infatti anche il test del chi quadrato che viene utilizzato per verificare l’indipendenza tra le variabili e la bontà di adattamento ad una distribuzione teorica. Ad esempio, il test Chi-quadrato può essere utilizzato per determinare se i dati di un campione sono conformi a una distribuzione di Poisson.

Nell’analisi di regressione lineare, la distribuzione chi-quadrato viene utilizzata anche per stimare la media di una popolazione distribuita normalmente e per stimare la pendenza della linea di studio della regressione lineare.

Infine, anche la distribuzione Chi quadrato partecipa all’analisi della varianza, attraverso la sua relazione con la distribuzione F di Snedecor.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più