Distribuzione t di student
Questo articolo spiega cos’è la distribuzione t di Student e a cosa serve. Inoltre, viene mostrato il grafico della distribuzione t di Student e quali sono le caratteristiche di questo tipo di distribuzione di probabilità.
Qual è la distribuzione di Student?
La distribuzione t di Student è una distribuzione di probabilità ampiamente utilizzata in statistica. Nello specifico, la distribuzione t di Student viene utilizzata nel test t di Student per determinare la differenza tra le medie di due campioni e per stabilire intervalli di confidenza.
La distribuzione t di Student fu sviluppata dallo statistico William Sealy Gosset nel 1908 con lo pseudonimo di “Student”.
La distribuzione t di Student è definita dal numero di gradi di libertà, ottenuti sottraendo un’unità dal numero totale di osservazioni. Pertanto, la formula per determinare i gradi di libertà della distribuzione t di Student è ν=n-1 .
![\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png "Rendered by QuickLaTeX.com")
Grafico della distribuzione t di Student
Ora che conosciamo la definizione della distribuzione t di Student, vediamo qual è il suo grafico. Quindi, di seguito puoi vedere graficamente diversi esempi di distribuzioni t di Student con diversi gradi di libertà.
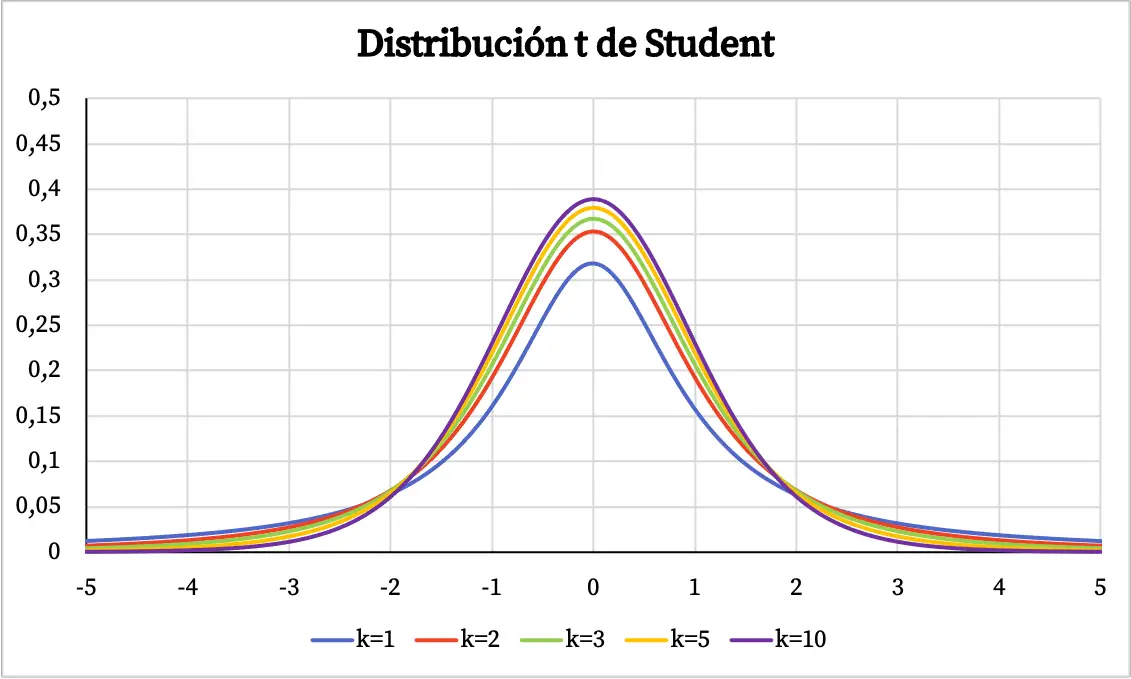
Dal grafico della distribuzione t di Student si possono dedurre le seguenti proprietà:
- La distribuzione t di Student è simmetrica centrata su 0 e ha una forma a campana.
- La distribuzione t di Student è più dispersa rispetto alla distribuzione normale, ovvero la curva della distribuzione t di Student è più ampia.
- Maggiori sono i gradi di libertà della distribuzione t di Student, minore è la sua dispersione.
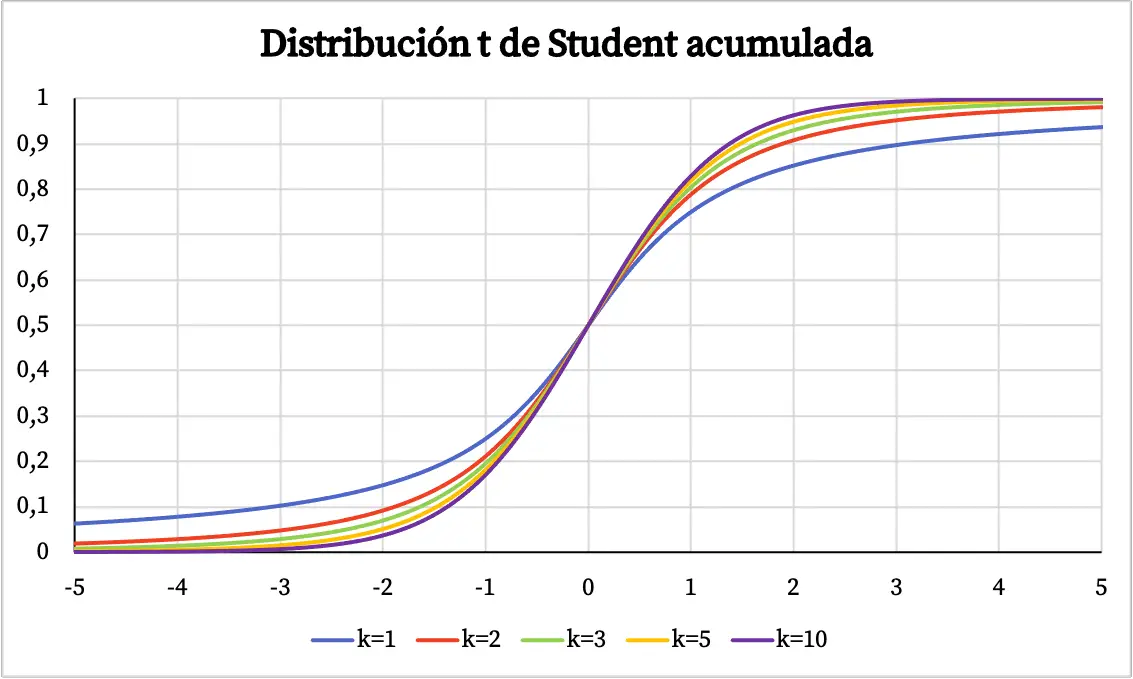
Nel grafico sopra, la funzione di densità della distribuzione t di Student è stata tracciata rispetto ai suoi gradi di libertà. Tuttavia, puoi vedere di seguito come varia la funzione di probabilità cumulativa della distribuzione t di Student:
Caratteristiche della distribuzione t di Student
Le caratteristiche più importanti della distribuzione t di Student sono mostrate di seguito.
- Il dominio della distribuzione t di Student è costituito da numeri reali.
- Per le distribuzioni t di Student con più di un grado di libertà, la media della distribuzione è uguale a 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> La varianza della distribuzione t di Student può essere calcolata utilizzando la seguente espressione:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> La mediana e la moda della distribuzione t di Student, indipendentemente dal numero di gradi di libertà, sono sempre 0.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png "Rendered by QuickLaTeX.com")
- La funzione di densità della distribuzione t di Student è definita dalla seguente formula:
![\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8c0f1e97a8e407e8b9e2b00ba93aee0e_l3.png "Rendered by QuickLaTeX.com")
- La funzione di distribuzione di probabilità cumulativa della distribuzione t di Student è definita dalla seguente formula:
![\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png "Rendered by QuickLaTeX.com")
- Per le distribuzioni t di Student con gradi di libertà maggiori di 3, il coefficiente di asimmetria è zero perché è una distribuzione simmetrica.
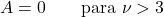
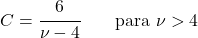Applicazioni della distribuzione t di Student
La distribuzione t di Student è una distribuzione di probabilità ampiamente utilizzata in statistica. Esiste infatti anche il test t di Student, che viene utilizzato per verificare ipotesi e intervalli di confidenza.
Pertanto, la distribuzione t di Student permette di analizzare la differenza tra le medie di due campioni, più precisamente, viene utilizzata per determinare se due campioni hanno medie significativamente diverse. Allo stesso modo, il test t di Student viene utilizzato per scoprire se la retta ottenuta da un’analisi di regressione lineare ha una pendenza o meno.
In breve, le applicazioni della distribuzione t di Student si basano sull’analisi di insiemi di dati che teoricamente seguono una distribuzione normale ma il numero totale di osservazioni è troppo piccolo per utilizzare questo tipo di distribuzione.
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più