Mle per una distribuzione di poisson (passo dopo passo)
La stima di massima verosimiglianza (MLE) è un metodo che può essere utilizzato per stimare i parametri di una determinata distribuzione.
Questo tutorial spiega come calcolare l’MLE per il parametro λ di una distribuzione di Poisson .
Passaggio 1: scrivere il PDF.
Innanzitutto, scrivi la funzione di densità di probabilità della distribuzione di Poisson:
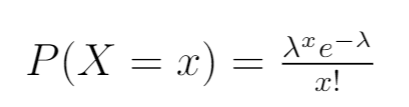
Passaggio 2: Scrivi la funzione di verosimiglianza.
Successivamente, scrivi la funzione di verosimiglianza. Questo è semplicemente il prodotto della PDF per i valori osservati x 1 , …, x n .
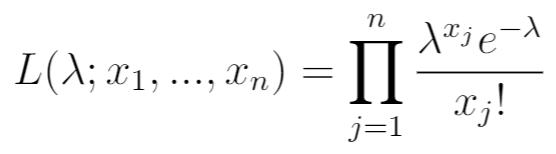
Passaggio 3: Scrivi la funzione di verosimiglianza del logaritmo naturale.
Per semplificare i calcoli possiamo scrivere la funzione di verosimiglianza naturale:
Passo 4: Calcola la derivata della funzione di verosimiglianza naturale rispetto a λ.
Possiamo quindi calcolare la derivata della funzione di verosimiglianza rispetto al parametro λ:
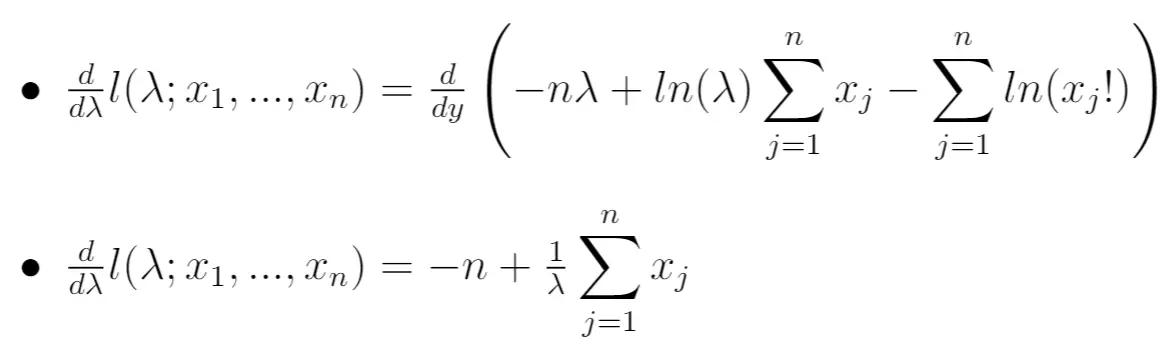
Passaggio 5: imposta la derivata uguale a zero e risolvi rispetto a λ.
Infine, impostiamo la derivata del passaggio precedente uguale a zero e risolviamo semplicemente rispetto a λ:
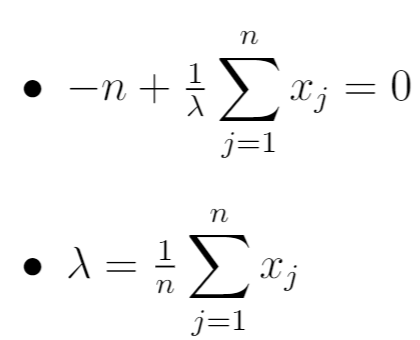
Pertanto la MLE risulta essere:
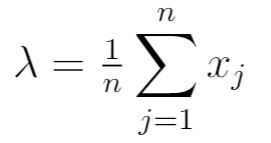
Ciò equivale alla media campionaria delle n osservazioni nel campione.
Risorse addizionali
Un’introduzione alla distribuzione di Poisson
Calcolatore della distribuzione dei pesci
Come utilizzare la distribuzione di Poisson in Excel
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più