Cos'è una distribuzione campionaria?

Immagina che ci sia una popolazione di 10.000 delfini e che il peso medio di un delfino in quella popolazione sia di 300 libbre.

Se prendiamo un semplice campione casuale di 50 delfini da questa popolazione, potremmo scoprire che il peso medio dei delfini in questo campione è di 305 libbre.

Quindi, se prendiamo un altro semplice campione casuale di 50 delfini, potremmo scoprire che il peso medio dei delfini in questo campione è di 295 libbre.

Ogni volta che prendiamo un semplice campione casuale di 50 delfini, è probabile che il peso medio dei delfini nel campione sia vicino alla media della popolazione di 300 libbre, ma non esattamente 300 libbre.

Immaginiamo di prendere 200 semplici campioni casuali di 50 delfini da questa popolazione e di creare un istogramma del peso medio di ciascun campione:

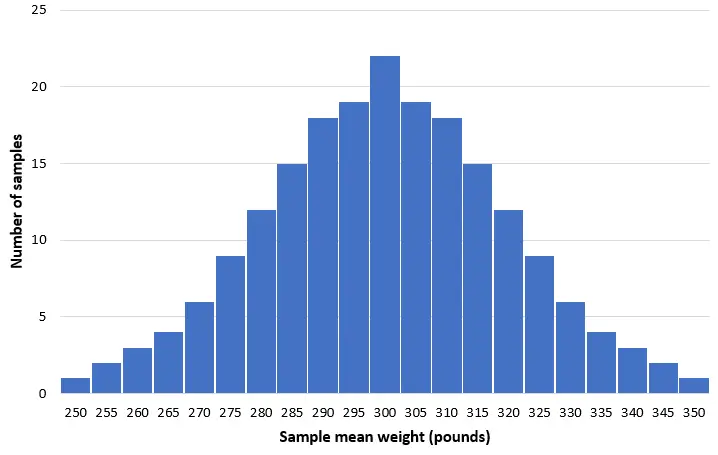
Nella maggior parte dei campioni, il peso medio sarà vicino a 300 libbre. In rari casi, potremmo prelevare un campione pieno di piccoli delfini il cui peso medio è di soli 250 libbre. Oppure potremmo prendere un campione pieno di delfini tursiopi che pesano in media 350 libbre. In generale, la distribuzione delle medie campionarie sarà approssimativamente normale, con il centro della distribuzione situato nel vero centro della popolazione.

Questa distribuzione delle medie campionarie è nota come distribuzione campionaria della media e ha le seguenti proprietà:

_µx = µ

dove _μx è la media campionaria e μ è la media della popolazione.

_σx = σ/√n

dove σ _x è la deviazione standard del campione, σ è la deviazione standard della popolazione e n è la dimensione del campione.

Ad esempio, in questa popolazione di delfini, sappiamo che il peso medio è μ = 300. Quindi la media della distribuzione campionaria è μ _x = 300 .

Supponiamo di sapere anche che la deviazione standard della popolazione è di 18 libbre. La deviazione standard del campione è quindi σ _x = 18/ √50 = 2.546 .

Distribuzione campionaria della proporzione

Considera la stessa popolazione di 10.000 delfini. Supponiamo che il 10% dei delfini sia nero e il resto sia grigio. Supponiamo di prendere un semplice campione casuale di 50 delfini e di scoprire che il 14% dei delfini in quel campione sono neri. Successivamente, prendiamo un altro semplice campione casuale di 50 delfini e scopriamo che l’8% dei delfini in questo campione sono neri.

Immaginiamo di prendere 200 campioni casuali semplici di 50 delfini da questa popolazione e di creare un istogramma della proporzione di delfini neri in ciascun campione:

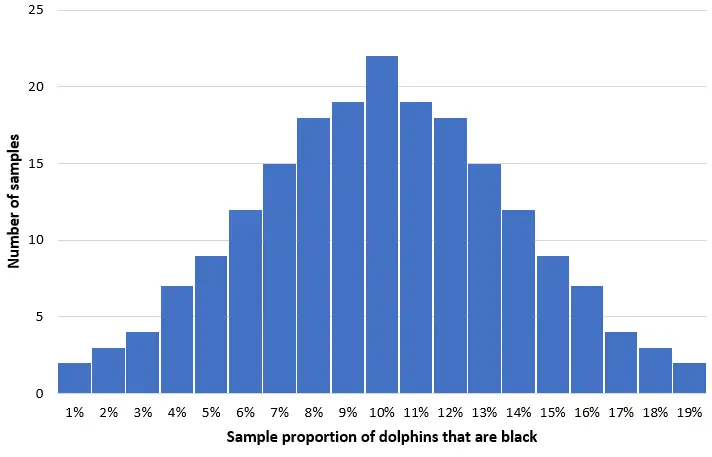
Nella maggior parte dei campioni la percentuale di delfini neri sarà vicina alla popolazione effettiva del 10%. La distribuzione della proporzione del campione di delfini neri sarà approssimativamente normale, con il centro della distribuzione situato nel vero centro della popolazione.

Questa distribuzione delle proporzioni campionarie è nota come distribuzione campionaria delle proporzioni e ha le seguenti proprietà:

_µp = P

dove p è la proporzione campionaria e P è la proporzione della popolazione.

σ _p = √ (P)(1-P) / n

dove P è la proporzione della popolazione e n è la dimensione del campione.

Ad esempio, in questa popolazione di delfini sappiamo che la percentuale reale di delfini neri è del 10% = 0,1. Pertanto, la media della distribuzione campionaria proporzionale è μ _p = 0,1 .

Supponiamo di sapere anche che la deviazione standard della popolazione è di 18 libbre. Pertanto, la deviazione standard del campione è σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Stabilire la normalità

Per utilizzare le formule di cui sopra, la distribuzione campionaria deve essere normale.

Secondo il teorema del limite centrale , la distribuzione campionaria di una media campionaria è approssimativamente normale se la dimensione del campione è sufficientemente grande, anche se la distribuzione della popolazione non è normale . Nella maggior parte dei casi, riteniamo che una dimensione del campione pari o superiore a 30 sia sufficientemente ampia.

La distribuzione campionaria di una proporzione campionaria è approssimativamente normale se il numero atteso di successi e fallimenti è almeno 10.

Esempi

Possiamo usare le distribuzioni campionarie per calcolare le probabilità.

Esempio 1: una determinata macchina crea cookie. La distribuzione del peso di questi biscotti è sbilanciata verso destra con una media di 10 once e una deviazione standard di 2 once. Se prendiamo un semplice campione casuale di 100 biscotti prodotti da questa macchina, qual è la probabilità che il peso medio dei biscotti in questo campione sia inferiore a 9,8 once?

Passaggio 1: stabilire la normalità.

Dobbiamo garantire che la distribuzione campionaria delle medie campionarie sia normale. Poiché la dimensione del nostro campione è maggiore o uguale a 30, secondo il teorema del limite centrale, possiamo assumere che la distribuzione campionaria delle medie campionarie sia normale.

Passo 2: Trova la media e la deviazione standard della distribuzione campionaria.

_µx = µ

_σx = σ/√n

_μx = 10 once

σ _x = 2/ √100 = 2/10 = 0,2 oncia

Passaggio 3: utilizzare il calcolatore dell’area Z-Score per determinare la probabilità che il peso medio dei biscotti in questo campione sia inferiore a 9,8 once.

Inserisci i seguenti numeri nel calcolatore dell’area del punteggio Z. Puoi lasciare vuoto “Punteggio grezzo 2” poiché in questo esempio troviamo solo un numero.

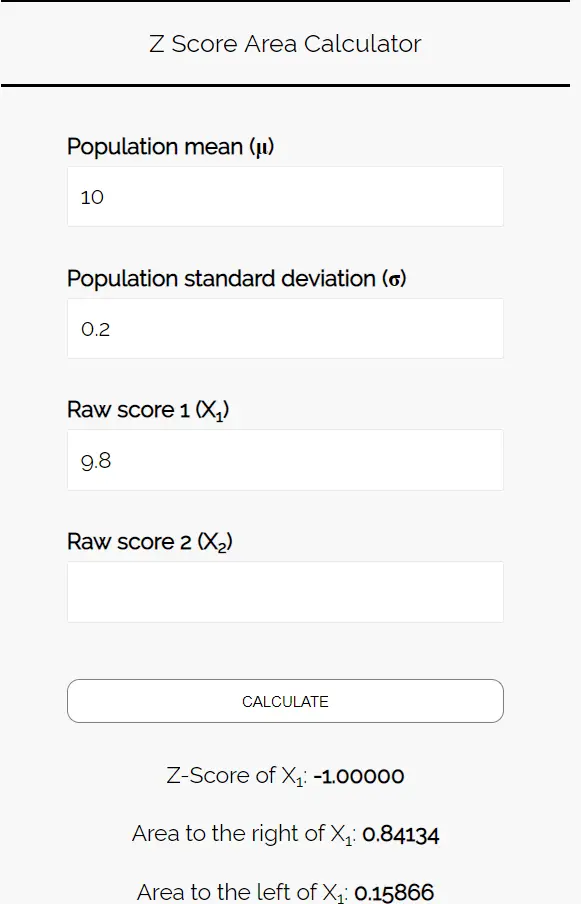
Poiché vogliamo conoscere la probabilità che il peso medio dei biscotti in questo campione sia inferiore a 9,8 once, siamo interessati all’area a sinistra di 9,8. Il calcolatore ci dice che questa probabilità è 0,15866 .

Esempio 2: secondo uno studio condotto a livello scolastico, l’87% degli studenti di una determinata scuola preferisce la pizza al gelato. Supponiamo di prendere un semplice campione casuale di 200 studenti. Qual è la probabilità che la percentuale di studenti che preferiscono la pizza sia inferiore all’85%?

Passaggio 1: stabilire la normalità.

Ricordiamo che la distribuzione campionaria di una proporzione campionaria è approssimativamente normale se il numero atteso di “successi” e “fallimenti” è almeno 10.

In questo caso, il numero previsto di studenti che preferiranno la pizza è 87% * 200 studenti = 174 studenti. Il numero previsto di studenti che non preferiranno la pizza è del 13% * 200 studenti = 26 studenti. Poiché entrambi questi numeri sono almeno 10, possiamo assumere che la distribuzione campionaria della proporzione di studenti che preferiranno la pizza sia approssimativamente normale.

Passo 2: Trova la media e la deviazione standard della distribuzione campionaria.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Passaggio 3: utilizzare il calcolatore dell’area Z-Score per determinare la probabilità che la percentuale di studenti che preferiscono la pizza sia inferiore all’85%.

Inserisci i seguenti numeri nel calcolatore dell’area del punteggio Z. Puoi lasciare vuoto “Punteggio grezzo 2” poiché in questo esempio troviamo solo un numero.

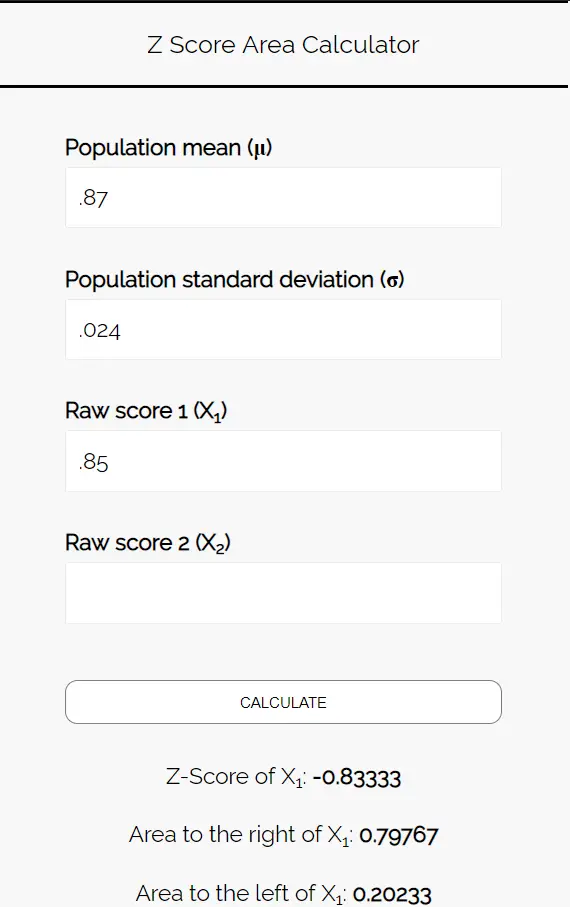
Poiché vogliamo conoscere la probabilità che la percentuale di studenti che preferiscono la pizza sia inferiore all’85%, siamo interessati all’area a sinistra di 0,85. Il calcolatore ci dice che questa probabilità è 0,20233 .