Un'introduzione alla distribuzione di poisson

La distribuzione di Poisson è una delle distribuzioni più popolari in statistica.

Per comprendere la distribuzione di Poisson, è utile prima comprendere gli esperimenti di Poisson.

Esperimenti sui pesci

Un esperimento di Poisson è un esperimento che ha le seguenti proprietà:

• Si può contare il numero dei successi dell’esperimento.
• È noto il numero medio di successi avvenuti durante uno specifico intervallo di tempo (o spazio).
• Ogni risultato è indipendente.
• La probabilità che si verifichi un successo è proporzionale alla dimensione dell’intervallo.

Un esempio di esperimento di Poisson è il numero di nascite all’ora in un dato ospedale. Ad esempio, supponiamo che un particolare ospedale abbia una media di 10 nascite all’ora. Questo è un esperimento di Poisson perché ha le seguenti quattro proprietà:

• Si può contare il numero dei successi dell’esperimento – Possiamo contare il numero delle nascite.
• È noto il numero medio di nascite che si verificano durante un determinato intervallo di tempo – È noto che ci sono in media 10 nascite all’ora.
• Ogni risultato è indipendente – La probabilità che una madre partorisca in una determinata ora è indipendente dalla probabilità che un’altra madre partorisca.
• La probabilità che si verifichi un successo è proporzionale alla dimensione dell’intervallo: più lungo è l’intervallo di tempo, maggiore è la probabilità che si verifichi una nascita.

Possiamo utilizzare la distribuzione di Poisson per rispondere a domande sulle probabilità relative a questo esperimento di Poisson come:

• Qual è la probabilità che avvengano più di 12 nascite in una data ora?
• Qual è la probabilità che avvengano meno di 5 nascite in una data ora?
• Qual è la probabilità che in una data ora avvengano tra 8 e 11 nascite?

La distribuzione dei pesci

La distribuzione di Poisson descrive la probabilità di ottenere k successi durante un dato intervallo di tempo.

Se una variabile casuale X segue una distribuzione di Poisson, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = λ ^k * e ^{– λ} / k!

Oro:

• λ: numero medio di successi che si verificano durante un intervallo specifico
• k: numero di successi
• e: una costante pari a circa 2,71828

Ad esempio, supponiamo che in un particolare ospedale si verifichino in media 2 nascite all’ora. Possiamo usare la formula sopra per determinare la probabilità di sperimentare 0, 1, 2, 3 nascite, ecc. in una determinata ora:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Possiamo calcolare la probabilità di un numero qualsiasi di nascite fino all’infinito. Creiamo quindi un semplice istogramma per visualizzare questa distribuzione di probabilità:

Calcolo delle probabilità di Poisson cumulative

È semplice calcolare una singola probabilità di Poisson (ad esempio la probabilità che in un ospedale si verifichino 3 nascite in una determinata ora) utilizzando la formula precedente, ma per calcolare le probabilità di Poisson cumulative dobbiamo aggiungere le probabilità individuali.

Ad esempio, supponiamo di voler conoscere la probabilità che in ospedale si verifichino 1 o meno parti in una determinata ora. Utilizzeremmo la seguente formula per calcolare questa probabilità:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Questa è chiamata probabilità cumulativa perché implica l’aggiunta di più probabilità. Possiamo calcolare la probabilità cumulativa di avere k nascite o meno in una data ora utilizzando una formula simile:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Possiamo calcolare queste probabilità cumulative per qualsiasi numero di nascite fino all’infinito. Possiamo quindi creare un istogramma per visualizzare questa distribuzione di probabilità cumulativa:

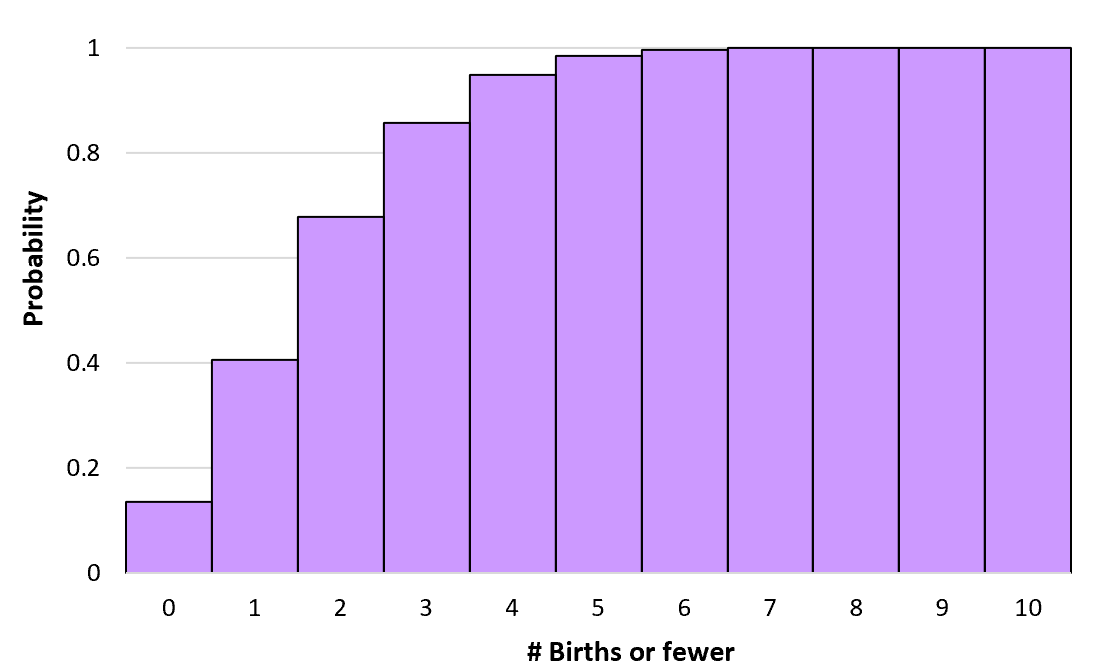
Proprietà della distribuzione di Poisson

La distribuzione di Poisson gode delle seguenti proprietà:

La media della distribuzione è λ .

Anche la varianza della distribuzione è λ .

La deviazione standard della distribuzione è √ λ .

Ad esempio, supponiamo che un ospedale abbia una media di 2 nascite all’ora.

Il numero medio di nascite attese in una data ora è λ = 2 nascite.

La varianza nel numero di nascite che ci aspettiamo è λ = 2 nascite.

Problemi relativi alla pratica della distribuzione del pesce

Utilizza i seguenti problemi pratici per verificare la tua conoscenza della distribuzione di Poisson.

Nota: utilizzeremo il calcolatore della distribuzione di Poisson per calcolare le risposte a queste domande.

Problema 1

Domanda: Sappiamo che un determinato sito web effettua 10 vendite all’ora. In una data ora, qual è la probabilità che il sito realizzi esattamente 8 vendite?

Risposta: Utilizzando il calcolatore della distribuzione di Poisson con λ = 10 e x = 8, troviamo che P(X=8) = 0,1126 .

Problema 2

Domanda: Sappiamo che un certo agente immobiliare effettua in media 5 vendite al mese. In un dato mese, qual è la probabilità che effettui più di 7 vendite?

Risposta: utilizzando il calcolatore della distribuzione di Poisson con λ = 5 e x = 7, troviamo che P(X>7) = 0,13337 .

Problema 3

Domanda: Sappiamo che in un determinato ospedale si effettuano 4 parti all’ora. In una data ora, qual è la probabilità che ci siano 4 nascite o meno?

Risposta: utilizzando il calcolatore della distribuzione di Poisson con λ = 4 e x = 4, troviamo che P(X≤4) = 0,62884 .

Risorse addizionali

I seguenti articoli spiegano come utilizzare la distribuzione di Poisson in diversi software statistici:

Come utilizzare la distribuzione di Poisson in R
Come utilizzare la distribuzione di Poisson in Excel
Come calcolare le probabilità di Poisson su una calcolatrice TI-84
Esempi reali della distribuzione di Poisson
Calcolatore della distribuzione dei pesci