Distribuzione campionaria della proporzione
Questo articolo spiega qual è la distribuzione campionaria della proporzione nelle statistiche. Allo stesso modo, troverai la formula di distribuzione del campionamento proporzionale e, inoltre, un esercizio risolto passo dopo passo.
Qual è la distribuzione campionaria della proporzione?
La distribuzione campionaria delle proporzioni (o distribuzione campionaria delle proporzioni ) è la distribuzione che risulta dal calcolo della proporzione di ciascun possibile campione di una popolazione. Cioè, le proporzioni campionarie di tutti i possibili campioni di una popolazione formano la distribuzione campionaria della proporzione.
In altre parole, la distribuzione della proporzione campionaria si ottiene studiando tutti i campioni che possono essere selezionati da una popolazione e derivando la proporzione campionaria di ciascun campione. Pertanto, l’insieme delle proporzioni campionarie calcolate costituisce la distribuzione campionaria della proporzione.
Nel caso ti stia chiedendo a cosa serve la distribuzione proporzionale della popolazione, in statistica viene utilizzata per calcolare la probabilità di avvicinarsi al valore della proporzione della popolazione quando si analizza un singolo campione.
Formula di distribuzione del campionamento proporzionale
Infatti, quando studiamo una parte di un campione, analizziamo casi di successo. Pertanto, la variabile casuale nello studio segue una distribuzione di probabilità binomiale .
Secondo il teorema del limite centrale, per grandi dimensioni (n>30) possiamo avvicinare una distribuzione binomiale ad una distribuzione normale. Pertanto, la distribuzione campionaria della proporzione approssima una distribuzione normale con i seguenti parametri:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
Oro
![]()
è la probabilità di successo e
![]()
è la probabilità di fallimento
![]()
.
Nota: una distribuzione binomiale può essere approssimata a una distribuzione normale solo se

![]()
E
![]()
.
Pertanto, poiché la distribuzione campionaria della proporzione può essere approssimata ad una distribuzione normale, la formula per calcolare l’eventuale probabilità relativa alla proporzione di un campione è:

Oro:
-

è la proporzione campionaria.
-

è la proporzione della popolazione.
-

è la probabilità di fallimento della popolazione,

.
-

è la dimensione del campione.
-

è una variabile definita dalla distribuzione normale standard N(0,1).
Esempio concreto di distribuzione campionaria proporzionale
Dopo aver visto la definizione di distribuzione campionaria proporzionale e quali sono le formule associate, di seguito viene fornito un esempio risolto passo dopo passo per comprendere appieno il concetto.
- Una società industriale acquista lotti di componenti da una fabbrica che afferma di produrre i componenti con solo il 3% di pezzi difettosi. Per verificarlo, l’azienda decide di analizzare un ordine di 500 pezzi. Qual è la probabilità di trovare più del 5% di parti difettose nel campione?
In questo caso, la proporzione della popolazione che vogliamo studiare è 0,03, quindi il parametro q equivale a 0,97.
![Rendered by QuickLaTeX.com \begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f4354c268853ec7b592bcacd23f3b214_l3.png)
Quindi, per trovare la probabilità che ce lo chiedono, dobbiamo calcolare la statistica corrispondente applicando la formula che abbiamo visto nella sezione precedente:
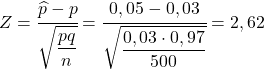
Pertanto la probabilità di ottenere più del 5% di pezzi difettosi equivale alla seguente probabilità:
![P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”></p>
</p>
<p> Cerchiamo infine la probabilità di P[Z≤2.62] nella <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-a5e5cff61f2cc97762df561b3e35a7ba_l3.png) tabella della distribuzione Z e calcoliamo la probabilità che il problema ci chiede:
tabella della distribuzione Z e calcoliamo la probabilità che il problema ci chiede:
![\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”></p>
</p>
<p> In conclusione, la probabilità di trovare più del 5% di parti difettose nel campione analizzato è pari allo 0,44%.</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-812f9b97c53e15da88b0cb7149f254c6_l3.png)
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più