Come creare un intervallo di confidenza utilizzando la distribuzione f
Per determinare se le varianze di due popolazioni sono uguali, possiamo calcolare il rapporto di varianza σ 2 1 / σ 2 2 , dove σ 2 1 è la varianza della popolazione 1 e σ 2 2 è la varianza della popolazione 2.
Per stimare il vero rapporto di varianza della popolazione, generalmente prendiamo un campione casuale semplice da ciascuna popolazione e calcoliamo il rapporto di varianza campionaria, s 1 2 / s 2 2 , dove s 1 2 e s 2 2 sono le varianze campionarie per il campione 1 e il campione . 2, rispettivamente.
Questo test presuppone che s 1 2 e s 2 2 siano calcolati da campioni indipendenti di dimensione n 1 e n 2 , entrambi provenienti da popolazioni distribuite normalmente.
Quanto più questo rapporto è lontano da uno, tanto più forte è l’evidenza di varianze disuguali all’interno della popolazione.
L’intervallo di confidenza (1-α)100% per σ 2 1 / σ 2 2 è definito come:
(s 1 2 / s 2 2 ) * F n 1 -1, n 2 -1, α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n 2 -1, n 1 -1, α/2
dove F n 2 -1, n 1 -1, α/2 e F n 1 -1, n 2 -1, α/2 sono i valori critici della distribuzione F per il livello di significatività α scelto.
I seguenti esempi illustrano come creare un intervallo di confidenza per σ 2 1 / σ 2 2 utilizzando tre metodi diversi:
- Per mano
- Utilizzare Microsoft Excel
- Utilizzo del software statistico R
Per ciascuno dei seguenti esempi, utilizzeremo le seguenti informazioni:
- α = 0,05
- n1 = 16
- n2 = 11
- s12 = 28,2
- s22 = 19,3
Creazione manuale di un intervallo di confidenza
Per calcolare manualmente un intervallo di confidenza per σ 2 1 / σ 2 2 , inseriremo semplicemente i numeri che abbiamo nella formula dell’intervallo di confidenza:
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
Gli unici numeri che ci mancano sono i valori critici. Fortunatamente, possiamo individuare questi valori critici nella tabella di distribuzione F :
F n2-1, n1-1, α/2 = F 10, 15, 0,025 = 3,0602
F n1-1, n2-1, α/2 = 1/ F 15, 10, 0,025 = 1 / 3,5217 = 0,2839
(clicca per ingrandire la tabella)
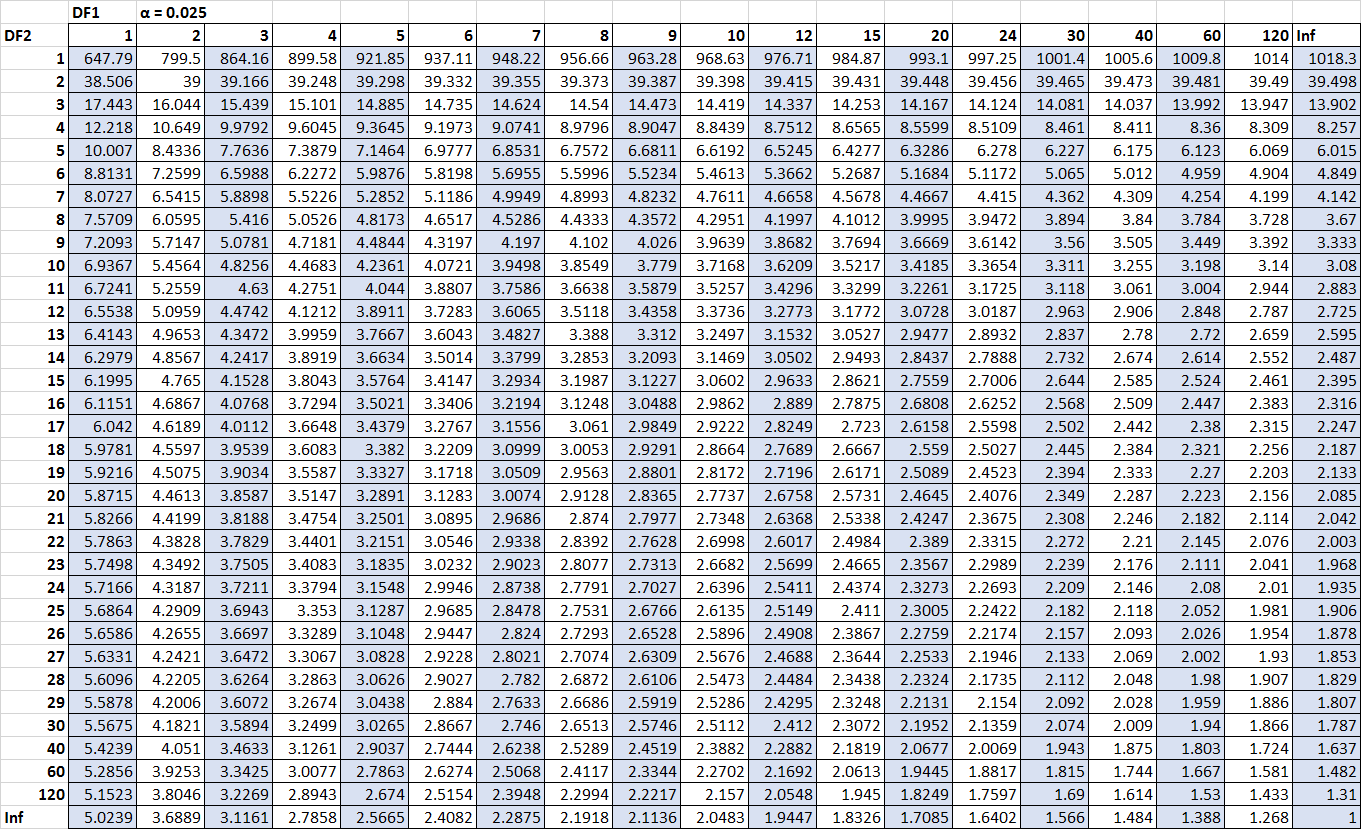
Ora possiamo inserire tutti i numeri nell’intervallo della formula di confidenza:
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
(28,2 / 19,3) * (0,2839) ≤ σ 2 1 / σ 2 2 ≤ (28,2 / 19,3) * (3,0602)
0,4148 ≤ σ 2 1 / σ 2 2 ≤ 4,4714
Pertanto, l’intervallo di confidenza al 95% per il rapporto delle varianze della popolazione è (0,4148, 4,4714) .
Creazione di un intervallo di confidenza utilizzando Excel
L’immagine seguente mostra come calcolare un intervallo di confidenza al 95% per il rapporto di varianza della popolazione in Excel. I limiti inferiore e superiore dell’intervallo di confidenza sono mostrati nella colonna E e la formula utilizzata per trovare i limiti inferiore e superiore è mostrata nella colonna F:
Pertanto, l’intervallo di confidenza al 95% per il rapporto delle varianze della popolazione è (0,4148, 4,4714) . Ciò corrisponde a ciò che abbiamo ottenuto quando abbiamo calcolato manualmente l’intervallo di confidenza.
Creazione di un intervallo di confidenza utilizzando R
Il codice seguente illustra come calcolare un intervallo di confidenza al 95% per il rapporto delle varianze della popolazione in R:
#define significance level, sample sizes, and sample variances alpha <- .05 n1 <- 16 n2 <- 11 var1 <- 28.2 var2 <- 19.3 #define F critical values upper_crit <- 1/qf(alpha/2, n1-1, n2-1) lower_crit <- qf(alpha/2, n2-1, n1-1) #find confidence interval lower_bound <- (var1/var2) * lower_crit upper_bound <- (var1/var2) * upper_crit #output confidence interval paste0("(", lower_bound, ", ", upper_bound, " )") #[1] "(0.414899337980266, 4.47137571035219 )"
Pertanto, l’intervallo di confidenza al 95% per il rapporto delle varianze della popolazione è (0,4148, 4,4714) . Ciò corrisponde a ciò che abbiamo ottenuto quando abbiamo calcolato manualmente l’intervallo di confidenza.
Risorse addizionali
Come leggere il quadro di distribuzione F
Come trovare il valore critico F in Excel