Cos’è una distribuzione di probabilità congiunta?

Una tabella di frequenza bidirezionale è una tabella che visualizza le frequenze (o “conteggi”) per due variabili categoriali.

Ad esempio, la seguente tabella a due vie mostra i risultati di un sondaggio in cui è stato chiesto a 100 persone quale sport preferissero: baseball, basket o football.

Le righe mostrano il sesso dell’intervistato e le colonne indicano lo sport scelto:

In questo esempio, ci sono due variabili: Sport e Sesso.

Una distribuzione di probabilità congiunta descrive semplicemente la probabilità che un dato individuo assuma due valori specifici per le variabili.

La parola “congiunto” deriva dal fatto che siamo interessati alla probabilità che due cose accadano contemporaneamente.

Ad esempio, su un totale di 100 individui, 13 erano maschi e sceglievano il baseball come sport preferito.

Quindi, diremmo che la probabilità congiunta che un dato individuo sia maschio e scelga il baseball come sport preferito è 13/100 = 0,13 o 13% .

Scritto in notazione matematica:

P(Sesso = Maschio, Sport = Baseball) = 13/100 = 0,13 .

Possiamo utilizzare questo processo per calcolare l’intera distribuzione di probabilità congiunta:

• P (Sesso = Maschio, Sport = Baseball) = 13/100 = 0,13
• P(Sesso = Maschio, Sport = Basket) = 15/100 = 0,15
• P(Sesso = Maschio, Sport = Calcio) = 20/100 = 0,20
• P (Sesso = Femmina, Sport = Baseball) = 23/100 = 0,23
• P(Sesso = Femmina, Sport = Basket) = 16/100 = 0,16
• P(Sesso = Femmina, Sport = Calcio) = 13/100 = 0,13

Nota che la somma delle probabilità è uguale a 1 , ovvero 100% .

Perché utilizzare una distribuzione di probabilità congiunta?

Le distribuzioni di probabilità congiunte sono utili perché spesso raccogliamo dati per due variabili (come sport e genere) e vogliamo rispondere a domande relative a entrambe le variabili.

Ad esempio, potremmo voler comprendere la probabilità che un dato individuo in una popolazione sia maschio e preferisca il baseball come sport preferito.

Oppure potremmo essere interessati a comprendere la probabilità che un dato individuo sia di sesso femminile e preferisca il calcio come sport preferito.

Una distribuzione di probabilità congiunta può aiutarci a rispondere a queste domande.

Utilizzare i seguenti esempi come pratica per comprendere meglio le distribuzioni di probabilità congiunte.

Esempio 1

La seguente tabella a due vie presenta i risultati di un sondaggio in cui è stato chiesto a 238 persone quale tipo di film preferissero:

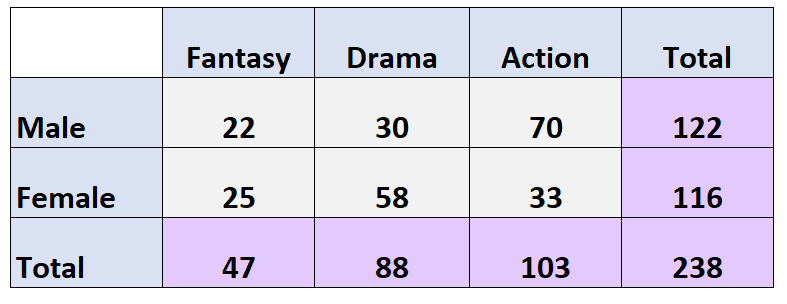
Domanda: Qual è la probabilità che un dato individuo sia donna e preferisca il dramma come genere cinematografico preferito?

Risposta: P (Sesso = Femmina, Genere = Dramma) = 58/238 = 0,244 = 24,4%

Esempio 2

La seguente tabella bidirezionale mostra i punteggi degli esami di 64 studenti in una classe in base al numero di ore trascorse a studiare:

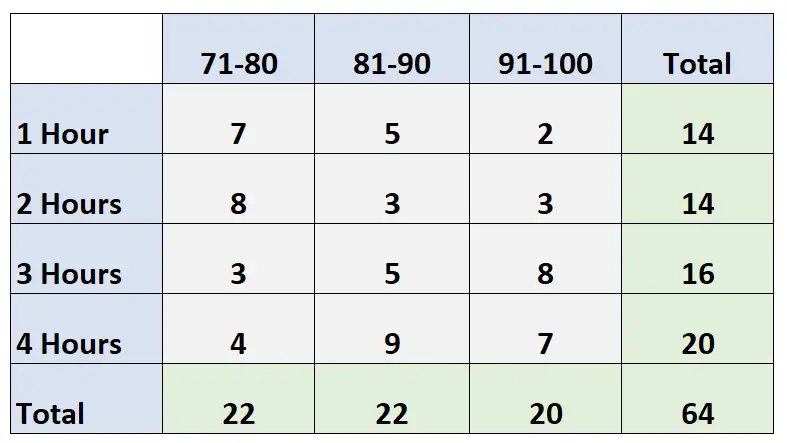
Domanda: Qual è la probabilità che un dato individuo studi per 2 ore e riceva un voto compreso tra 91 e 100?

Risposta: P (Studio = 2 ore, Punteggio = 91-100) = 3/64 = 0,047 = 4,7%

Risorse addizionali

Cos’è una distribuzione marginale?
Come trovare la frequenza relativa condizionale in una tabella a doppia entrata