Un'introduzione alla distribuzione di rayleigh

La distribuzione di Rayleigh è una distribuzione di probabilità continua utilizzata per modellare variabili casuali che possono assumere solo valori uguali o superiori a zero.

Ha la seguente funzione di densità di probabilità:

f(x; σ) = (x/σ ² )e ^{-x 2 /(2σ 2 )}

dove σ è il parametro di scala della distribuzione.

Proprietà della distribuzione di Rayleigh

La distribuzione di Rayleigh ha le seguenti proprietà:

• Media: σ√ π/2
• Deviazione: ((4-π)/2)σ ²
• Modo: σ

Poiché π ha un valore numerico noto, possiamo semplificare le proprietà come segue:

• Media: 1.253σ
• Deviazione: 0,429σ ²
• Modo: σ

Visualizzazione della distribuzione di Rayleigh

Il grafico seguente mostra la forma della distribuzione di Rayleigh poiché assume valori diversi per il parametro di scala:

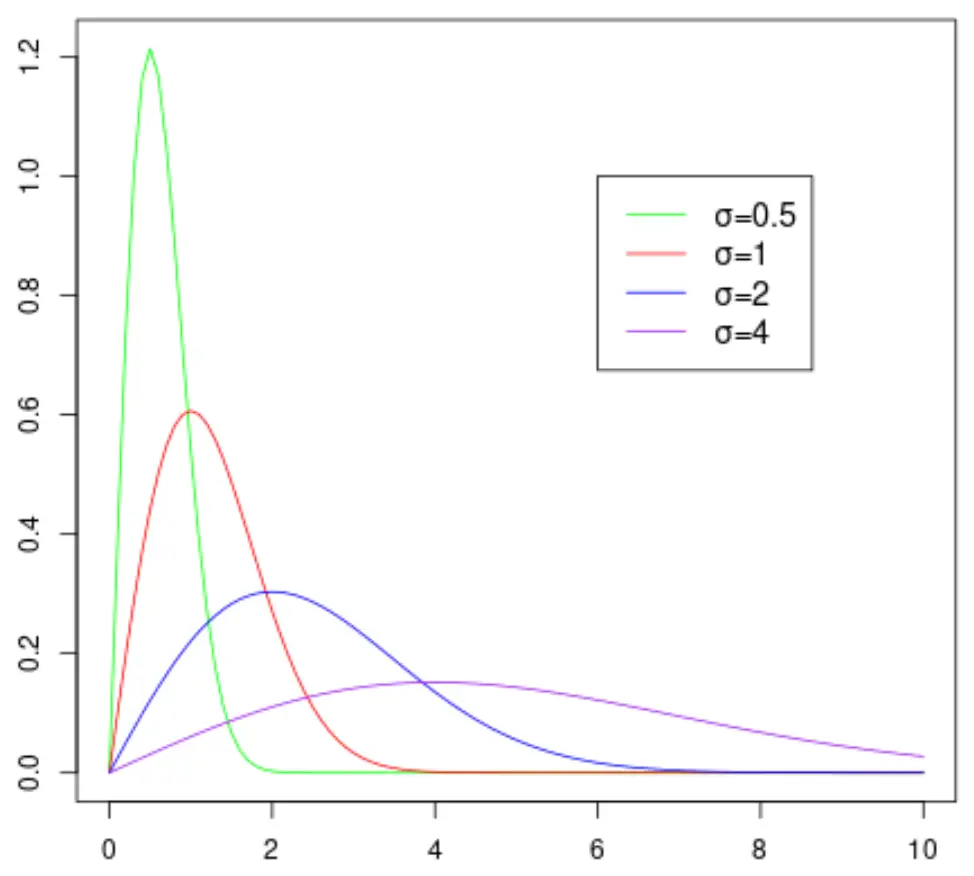
Si noti che maggiore è il valore del parametro di scala σ, più ampia diventa la distribuzione.

Bonus: per coloro che sono curiosi, abbiamo utilizzato il seguente codice R per generare il grafico sopra:

 #load VGAM package
library (VGAM)

#create density plots
curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green')
curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE)
curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE)
curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE)

#add legend
legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"),
       col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)

Rapporti con altre distribuzioni

La distribuzione di Rayleigh ha la seguente relazione con altre distribuzioni di probabilità:

1. Quando il parametro di scala (σ) è uguale a 1, la distribuzione di Rayleigh è uguale a una distribuzione Chi-quadrato con 2 gradi di libertà.

2. La distribuzione di Rayleigh è un caso speciale della distribuzione di Weibull con parametro di forma k = 2.

3. La distribuzione di Rayleigh con parametro di scala σ è uguale alla distribuzione di Rice con Rice(0, σ).

Applicazioni

In pratica la distribuzione di Rayleigh viene utilizzata in varie applicazioni, tra cui:

1. La distribuzione di Rayleigh viene utilizzata per modellare il comportamento delle onde nell’oceano, compreso il tempo impiegato dalle onde per raggiungere la cresta e l’altezza massima raggiunta dalle onde.

2. La distribuzione di Rayleigh viene utilizzata per modellare il comportamento dei dati di fondo nella risonanza magnetica, più comunemente nota come MRI.

3. La distribuzione di Rayleigh viene utilizzata nel campo della nutrizione per modellare la relazione tra i livelli di nutrienti e la risposta nutrizionale negli esseri umani e negli animali.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive su altre distribuzioni nelle statistiche:

Un’introduzione alla distribuzione normale
Un’introduzione alla distribuzione binomiale
Un’introduzione alla distribuzione di Poisson