Distribuzione snedecor f

Di Agosto 4, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è la distribuzione Snedecor F e a cosa serve. Inoltre, potrai vedere il grafico della distribuzione di Snedecor F e quali sono le sue proprietà statistiche.

Qual è la distribuzione Snedecor F?

La distribuzione F di Snedecor , chiamata anche distribuzione F di Fisher-Snedecor o semplicemente distribuzione F , è una distribuzione di probabilità continua utilizzata nell’inferenza statistica, in particolare nell’analisi della varianza.

Una delle proprietà della distribuzione F di Snedecor è che è definita dal valore di due parametri reali, m e n , che ne indicano i gradi di libertà. Pertanto, il simbolo della distribuzione Snedecor F è F m,n , dove m e n sono i parametri che definiscono la distribuzione.

F_{m,n}\qquad m,n>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”139″ style=”vertical-align: -6px;”></p> </p> <p> Matematicamente, la distribuzione F di Snedecor è uguale al quoziente tra una distribuzione chi-quadrato e i suoi gradi di libertà diviso per il quoziente tra un’altra distribuzione chi-quadrato e i suoi gradi di libertà. Pertanto, la formula che definisce la distribuzione Snedecor F è la seguente: </p> </p> <p class=\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}

La distribuzione F Fisher-Snedecor deve il suo nome allo statistico inglese Ronald Fisher e allo statistico americano George Snedecor.

Nelle statistiche, la distribuzione F Fisher-Snedecor ha diverse applicazioni. Ad esempio, la distribuzione F di Fisher-Snedecor viene utilizzata per confrontare diversi modelli di regressione lineare e questa distribuzione di probabilità viene utilizzata nell’analisi della varianza (ANOVA).

Diagramma di distribuzione Snedecor F

Una volta vista la definizione della distribuzione Snedecor F, di seguito vengono mostrati il grafico della sua funzione di densità e il grafico della sua probabilità cumulativa.

Nel grafico sottostante puoi vedere diversi esempi di distribuzioni Snedecor F con diversi gradi di libertà.

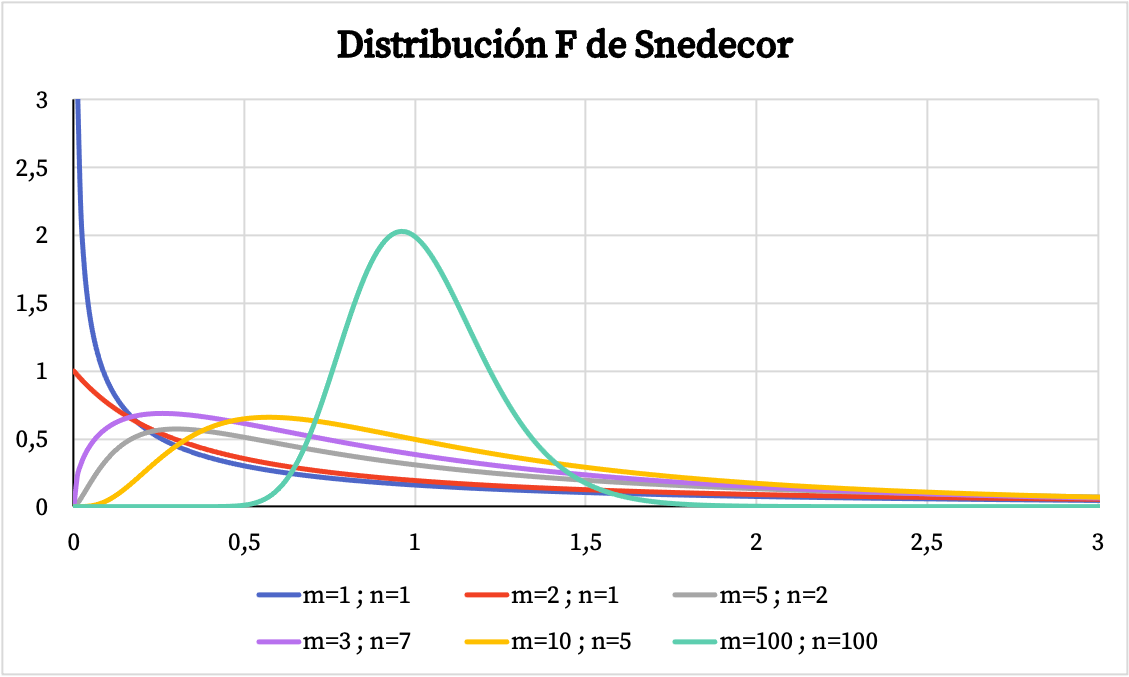
Grafico della distribuzione di Snedecor F

D’altra parte, nel grafico sottostante puoi vedere come varia il grafico della funzione di probabilità cumulativa della distribuzione Snedecor F a seconda dei suoi valori caratteristici.

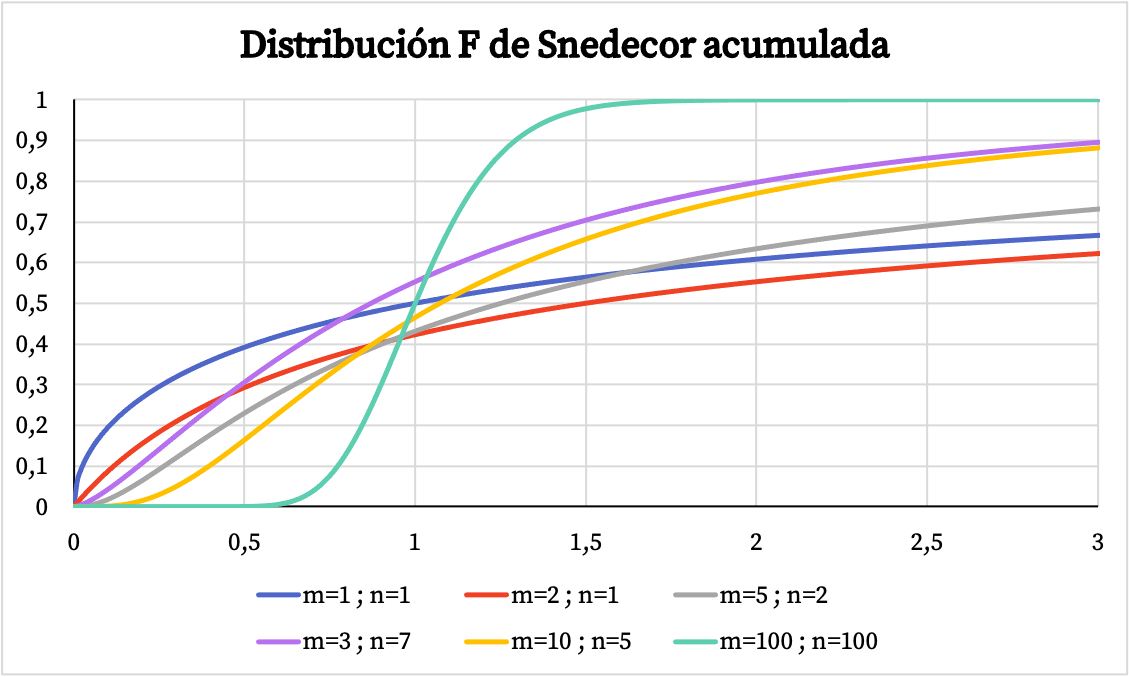
probabilità cumulativa della distribuzione Snedecor F

Caratteristiche della distribuzione Snedecor F

Infine, questa sezione presenta le caratteristiche più importanti della distribuzione Snedecor F.

  • I gradi di libertà della distribuzione Snedecor F, m e n , sono due parametri che definiscono la forma della distribuzione. Questi valori caratteristici della distribuzione Snedecor F sono numeri interi positivi.

\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Il dominio della distribuzione Snedecor F è costituito da tutti i numeri reali maggiori o uguali a zero.</li> </ul> <p class=x\in [0,+\infty)

  • Per valori di n maggiori di 2, la media della distribuzione Snedecor F è pari a n sulla sottrazione di n meno 2.

\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Quando il parametro <em>n</em> è maggiore di 2, la varianza della distribuzione Snedecor F può essere calcolata applicando la seguente formula:</li> </ul> <p class=\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Se il parametro <em>m</em> è maggiore di 2, la moda della distribuzione Snedecor F può essere calcolata con la seguente espressione:</li> </ul> <p class=Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2″ title=”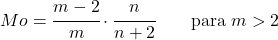Rendered by QuickLaTeX.com” height=”40″ width=”278″ style=”vertical-align: -14px;”></p> </p> <ul> <li> La formula per la funzione di densità della distribuzione Snedecor F è la seguente:</li> </ul> <p class=\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}

  • Se una variabile segue una distribuzione Snedecor F con gradi di libertà m e n , allora l’inverso di detta variabile segue una distribuzione Snedecor F con gli stessi gradi di libertà ma cambiando l’ordine dei suoi valori.

X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}

  • La distribuzione Student ha la seguente relazione con la distribuzione Snedecor F:

X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}

Informazioni sull'autore

Dr. Benjamin Anderson
Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Aggiungi un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *