Un'introduzione alla distribuzione geometrica

La distribuzione geometrica descrive la probabilità di sperimentare un certo numero di fallimenti prima di sperimentare il primo successo in una serie di prove Bernoulliane.

Una prova Bernoulli è un esperimento con solo due possibili esiti – “successo” o “fallimento” – e la probabilità di successo è la stessa ogni volta che l’esperimento viene condotto.

Un esempio di saggio di Bernoulli è il lancio di una moneta. La moneta può atterrare solo su due teste (potremmo chiamare testa un “colpo” e croce un “fallimento”) e la probabilità di successo su ogni lancio è 0,5, presupponendo che la moneta sia giusta.

Se una variabile casuale X segue una distribuzione geometrica, la probabilità di sperimentare k fallimenti prima di sperimentare il primo successo può essere trovata dalla seguente formula:

P(X=k) = (1-p) ^kp

Oro:

• k: numero di fallimenti prima del primo successo
• p: probabilità di successo in ciascuna prova

Ad esempio, supponiamo di voler sapere quante volte dobbiamo lanciare una moneta equilibrata finché non esce testa. Possiamo utilizzare la formula sopra per determinare la probabilità di riscontrare 0, 1, 2, 3 guasti, ecc. prima che la moneta esca testa:

Nota: la moneta può subire 0 “fallimento” se esce testa al primo lancio.

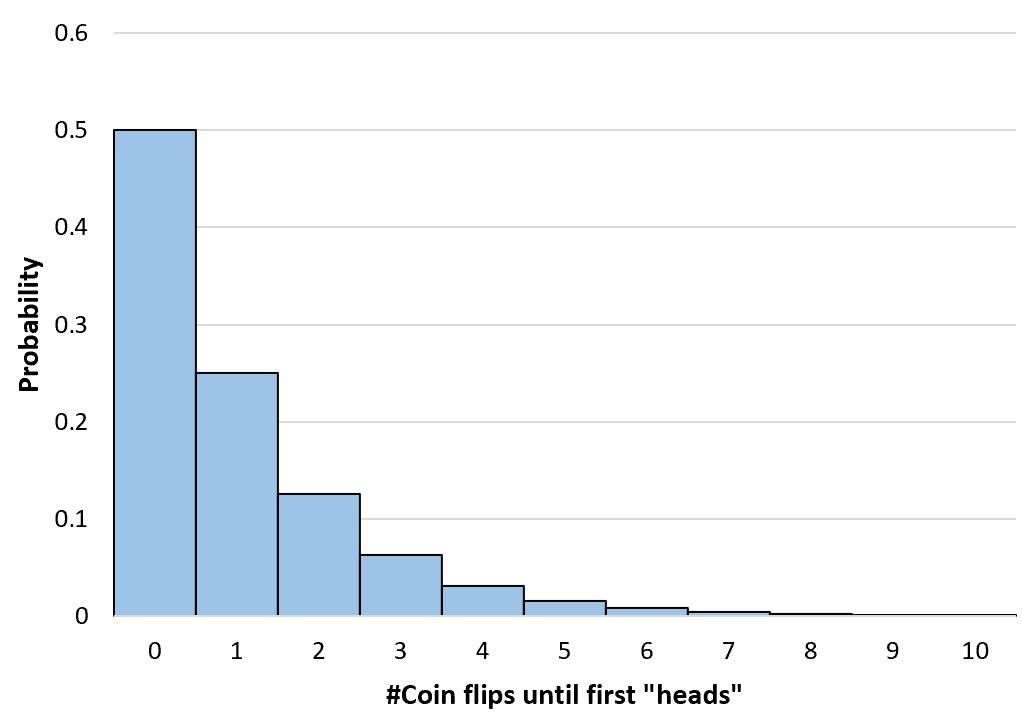
P(X=0) = (1-0,5) ⁰ (0,5) = 0,5

P(X=1) = (1-0,5) ¹ (0,5) = 0,25

P(X=2) = (1-0,5) ² (0,5) = 0,125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Possiamo calcolare la probabilità di un numero qualsiasi di lanci di moneta fino all’infinito. Creiamo quindi un semplice istogramma per visualizzare questa distribuzione di probabilità:

Calcolo delle probabilità geometriche cumulative

La probabilità cumulativa di riscontrare k o meno fallimenti fino al primo successo può essere trovata con la seguente formula:

P(X≤k) = 1 – (1-p) ^k+1

Oro:

• k: numero di fallimenti prima del primo successo
• p: probabilità di successo in ciascuna prova

Ad esempio, supponiamo di voler conoscere la probabilità che siano necessari tre o meno “mancati” prima che la moneta esca testa. Utilizzeremmo la seguente formula per calcolare questa probabilità:

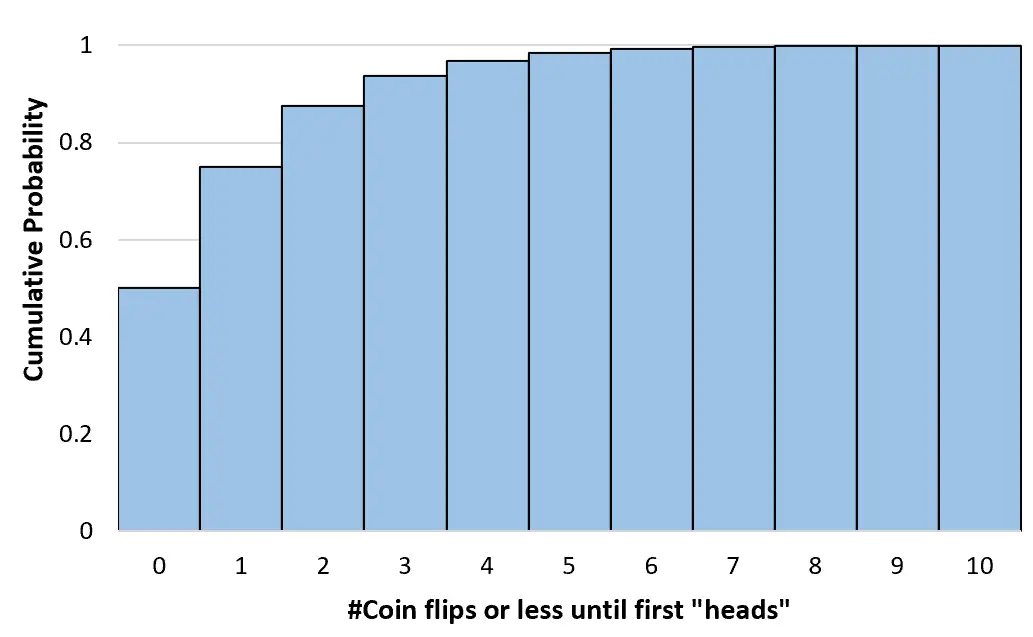
P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Possiamo calcolare ciascuna probabilità cumulativa utilizzando una formula simile:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0,5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Possiamo calcolare queste probabilità cumulative per qualsiasi numero di lanci di moneta fino all’infinito. Possiamo quindi creare un istogramma per visualizzare questa distribuzione di probabilità cumulativa:

Proprietà della distribuzione geometrica

La distribuzione geometrica ha le seguenti proprietà:

La media della distribuzione è (1-p) / p .

La varianza della distribuzione è (1-p) / p ² .

Per esempio:

Il numero medio di volte in cui ci aspettiamo che una moneta esca testa prima che esca croce sarebbe (1-p) / p = (1-.5) / .5 = 1 .

La varianza del numero di lanci fino a quando non esce testa sarebbe (1-p)/ ^p2 =(1-.5)/. ⁵² = 2 .

Problemi pratici di distribuzione geometrica

Utilizza i seguenti problemi pratici per testare la tua conoscenza della distribuzione geometrica.

Nota: utilizzeremo il calcolatore della distribuzione geometrica per calcolare le risposte a queste domande.

Problema 1

Domanda: Un ricercatore aspetta fuori da una biblioteca per chiedere alle persone se sostengono una determinata legge. La probabilità che una determinata persona sostenga la legge è p = 0,2. Qual è la probabilità che la quarta persona con cui parla il ricercatore sia la prima a sostenere la legge?

Risposta: Il numero di “fallimenti” fino al primo successo – ovvero il numero di persone che non sostengono la legge finché la prima persona non la sostiene – è 3. Quindi, utilizzando il calcolatore della distribuzione geometrica con p = 0,2 e x = 3 fallimenti, troviamo che P(X=3) = 0.10240 .

Problema 2

Domanda: Un ricercatore aspetta fuori da una biblioteca per chiedere alle persone se sostengono una determinata legge. La probabilità che una determinata persona sostenga la legge è p = 0,2. Qual è la probabilità che il ricercatore debba parlare con più di quattro persone per trovare qualcuno che sostenga la legge?

Risposta: Utilizzando il calcolatore della distribuzione geometrica con p = 0,2 ex = 4 guasti, troviamo che P(X>4) = 0,32768 .

Problema 3

Domanda: Un ricercatore aspetta fuori da una biblioteca per chiedere alle persone se sostengono una determinata legge. La probabilità che una determinata persona sostenga la legge è p = 0,2. Qual è il numero previsto di persone con cui il ricercatore dovrà parlare finché non troverà qualcuno che sostiene la legge?

Risposta: ricorda che la media della distribuzione geometrica è (1-p) / p . In questa situazione, la media sarebbe (1-.2) / .2 = 4 .