Come utilizzare la distribuzione geometrica in excel

La distribuzione geometrica descrive la probabilità di sperimentare un certo numero di fallimenti prima di sperimentare il primo successo in una serie di prove Bernoulliane.

Una prova Bernoulli è un esperimento con solo due possibili esiti – “successo” o “fallimento” – e la probabilità di successo è la stessa ogni volta che l’esperimento viene condotto.

Un esempio di saggio di Bernoulli è il lancio di una moneta. La moneta può atterrare solo su due teste (potremmo chiamare testa un “colpo” e croce un “fallimento”) e la probabilità di successo su ogni lancio è 0,5, presupponendo che la moneta sia giusta.

Se una variabile casuale X segue una distribuzione geometrica, la probabilità di sperimentare k fallimenti prima di sperimentare il primo successo può essere trovata dalla seguente formula:

P(X=k) = (1-p) ^kp

Oro:

• k: numero di fallimenti prima del primo successo
• p: probabilità di successo in ciascuna prova

Gli esempi seguenti mostrano come calcolare le probabilità relative alla distribuzione geometrica in Excel.

Esempio 1: lancia una moneta

Supponiamo di lanciare una moneta e di voler conoscere la probabilità che siano necessari esattamente tre “mancati” prima che una moneta esca testa.

Utilizzeremmo la seguente formula per calcolare questa probabilità:

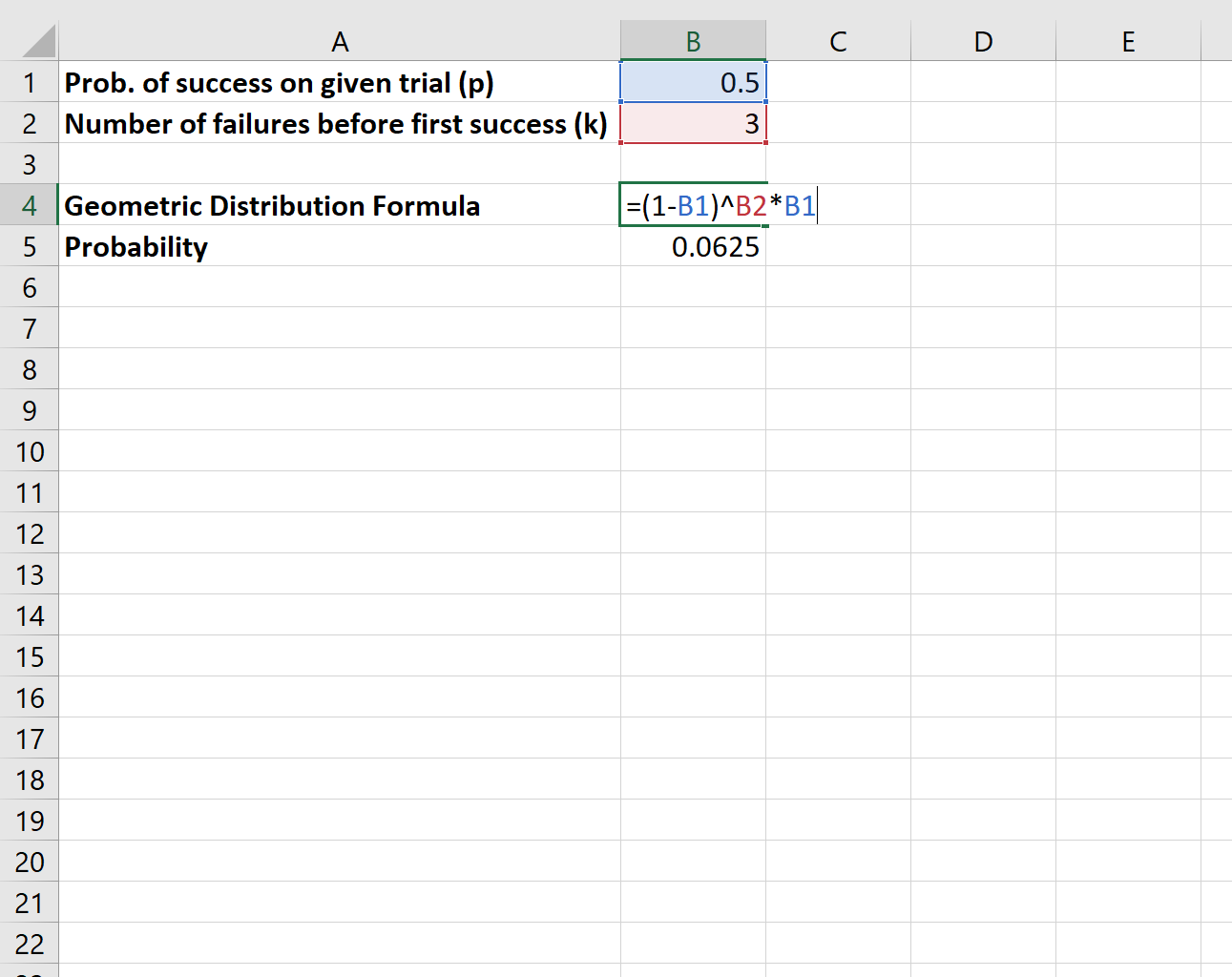
La probabilità che si verifichino tre “mancate” finché una moneta non esce testa è 0,0625 .

Esempio 2: Tiro libero

Supponiamo che un certo giocatore di basket effettui il 60% dei suoi tiri liberi. Qual è la probabilità che il giocatore sbagli quattro tiri liberi finché non ne effettua uno?

Utilizzeremmo la seguente formula per calcolare questa probabilità:

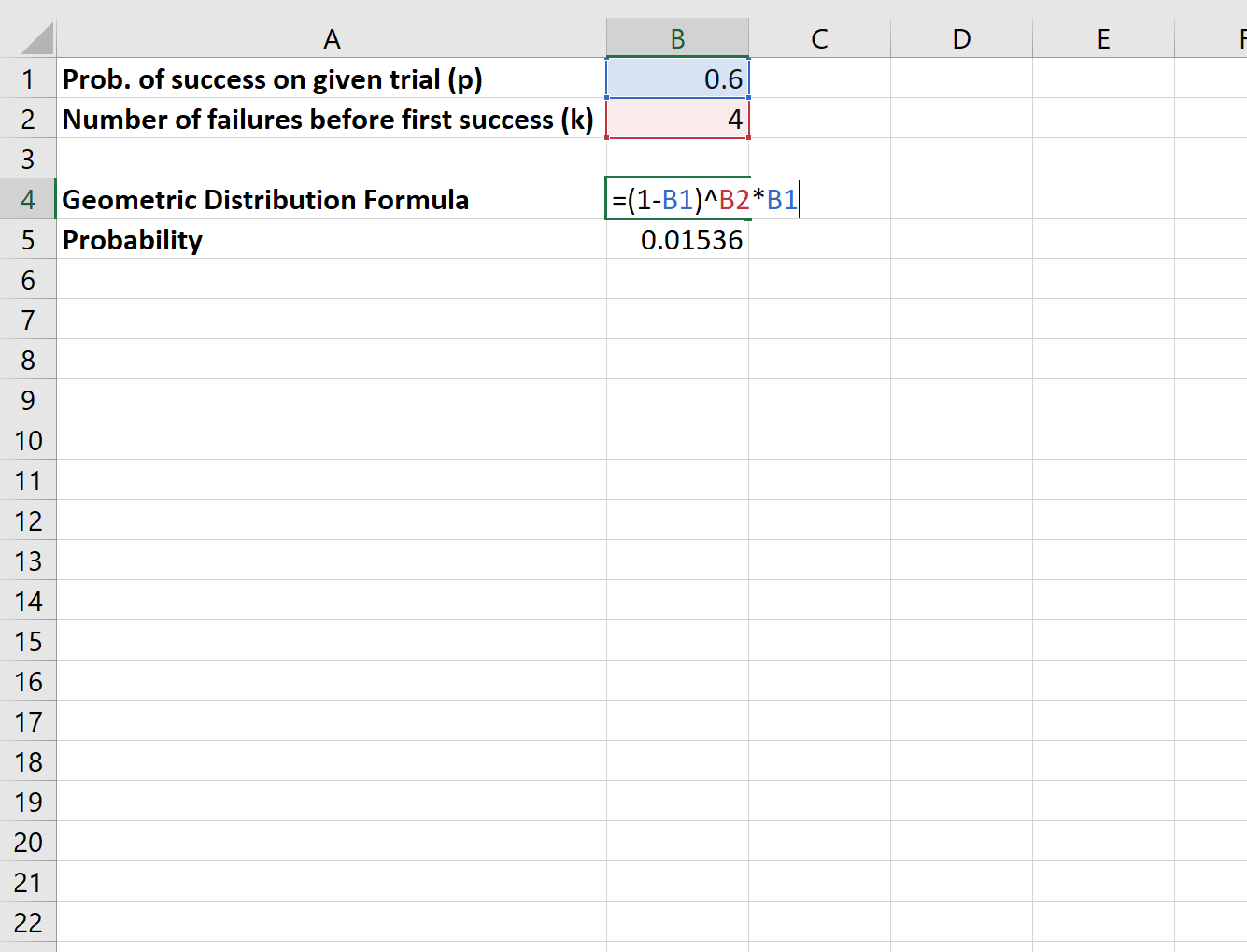
La probabilità che il giocatore sbagli quattro tiri liberi finché non ne effettua uno è 0,01536 .

Esempio 3: Sostenere una legge

Supponiamo che un ricercatore aspetti fuori da una biblioteca per chiedere alle persone se sostengono una determinata legge. La probabilità che una determinata persona sostenga la legge è p = 0,2. Qual è la probabilità che la quarta persona con cui parla il ricercatore sia la prima a sostenere la legge?

Utilizzeremmo la seguente formula per calcolare questa probabilità:

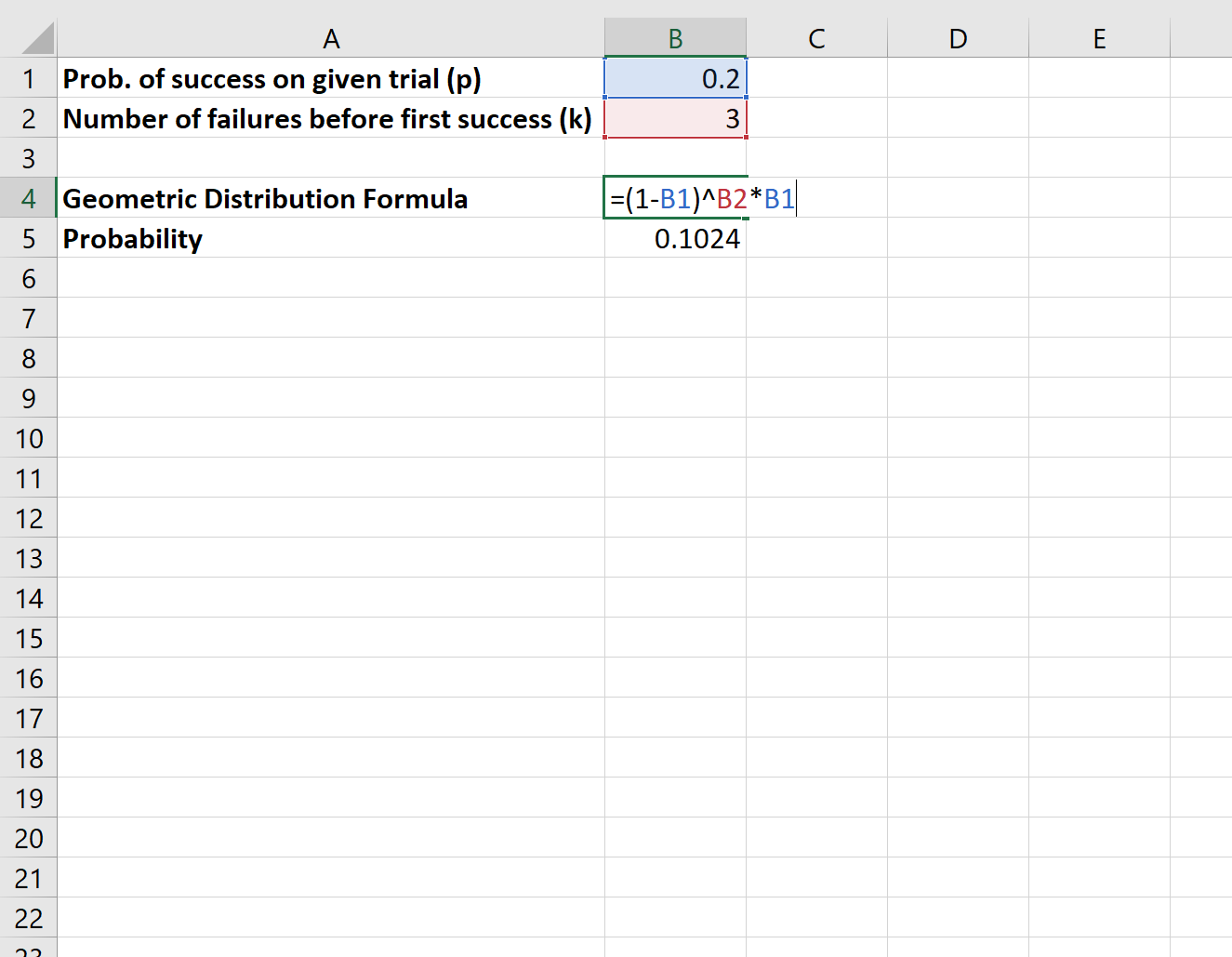
La probabilità che la quarta persona con cui parla il ricercatore sia la prima a sostenere la legge è 0,1024 .

Risorse addizionali

Un’introduzione alla distribuzione geometrica
Calcolatore della distribuzione geometrica
5 esempi concreti di distribuzione geometrica