Cos'è la distribuzione erlang?
La distribuzione di Erlang è una distribuzione di probabilità originariamente creata da AK Erlang per modellare il numero di chiamate telefoniche che un operatore di stazione di commutazione può ricevere simultaneamente.
La distribuzione viene utilizzata nell’ingegneria del traffico telefonico, nei sistemi di coda, nella biologia matematica e in altri campi per modellare una varietà di fenomeni del mondo reale.
Proprietà della distribuzione di Erlang
La distribuzione di Erlang ha la seguente funzione di densità di probabilità:
f(x; k, μ) = x k-1 e -x/μ / μ k (k-1)!
Oro:
- k: il parametro della forma. Deve essere un numero intero positivo.
- μ: il parametro di scala. Deve essere un numero reale positivo.
Si scopre che la distribuzione Erlang è un caso speciale della distribuzione Gamma quando il parametro di forma k è limitato solo a numeri interi reali positivi.
Si noti che il parametro di scala è il reciproco del parametro di velocità, λ, ovvero μ = 1/λ.
La distribuzione Erlang ha le seguenti proprietà:
- Media: k/λ
- Modalità: (k-1)/λ
- Differenza: k/λ 2
- Asimmetria: 2/√k
- Appiattimento: 6/k
La distribuzione Erlang ha le seguenti relazioni con altre distribuzioni:
- Quando il parametro di forma k è uguale a 1, la distribuzione Erlang è uguale alla distribuzione esponenziale .
- Quando il parametro di scala μ è uguale a 2, la distribuzione Erlang è uguale a una distribuzione Chi-quadrato con 2 gradi di libertà.
Visualizza la distribuzione Erlang
Il grafico seguente mostra la forma della distribuzione Erlang quando accetta parametri diversi:
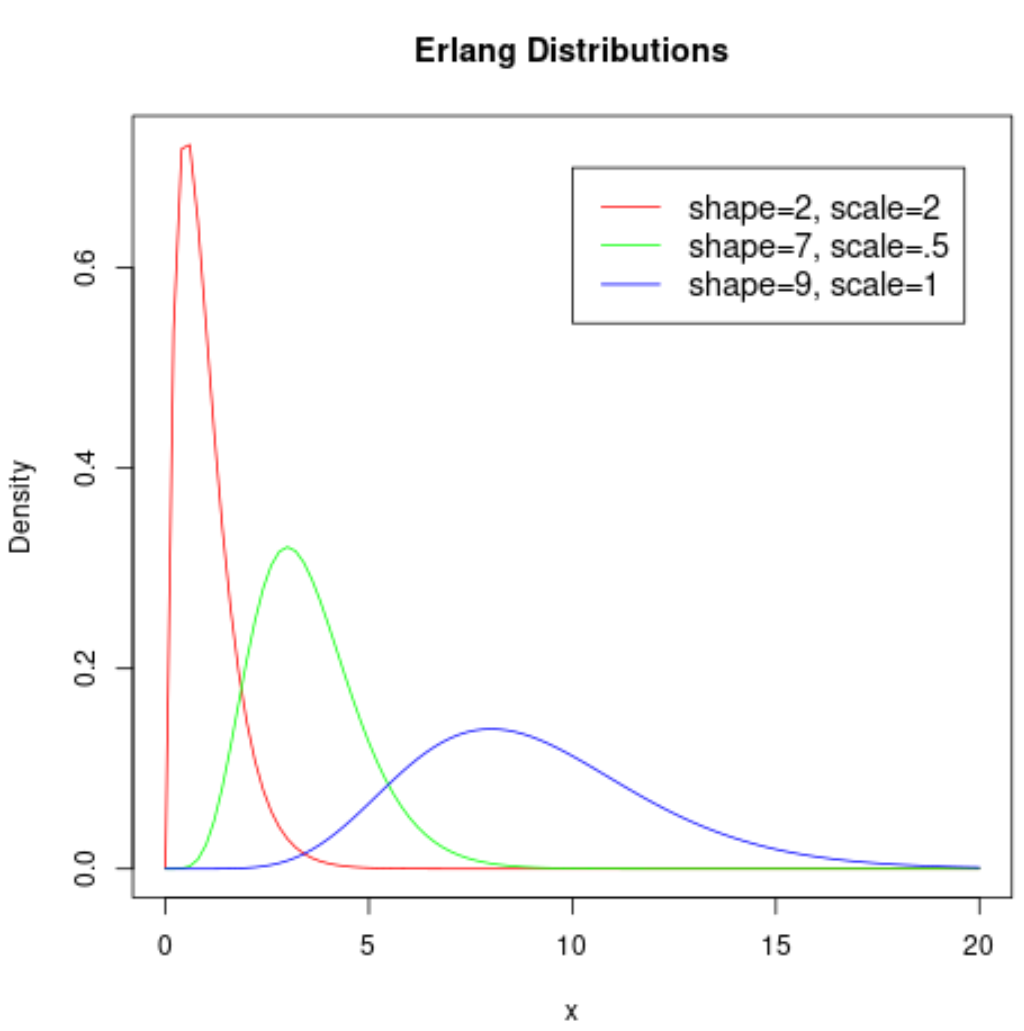
È interessante vedere quanto cambia la forma della distribuzione a seconda dei valori utilizzati per i parametri di forma e scala.
Nota: puoi trovare il codice R utilizzato per generare il grafico delle distribuzioni Erlang qui .
Caso d’uso
La distribuzione Erlang viene utilizzata in vari contesti del mondo reale, tra cui:
1. Call center
La distribuzione Erlang viene utilizzata per modellare il tempo che intercorre tra le chiamate in entrata in un call center e il numero previsto di chiamate.
Ciò consente ai call center di sapere quale dovrebbe essere la loro capacità di personale nei diversi orari della giornata in modo da poter gestire le chiamate in arrivo in modo tempestivo senza perdere denaro assumendo troppi dipendenti durante un turno. dato lavoro.
2.Parametri medici
La distribuzione di Erlang è ampiamente utilizzata per modellare la distribuzione della durata del ciclo cellulare, che ha molte applicazioni diverse in ambito medico.
3. Impostazioni di vendita al dettaglio
La distribuzione Erlang viene utilizzata dai rivenditori per modellare la frequenza dei ritardi nell’acquisto dei consumatori.
Ciò fornisce ai rivenditori e ad altre aziende un’idea della frequenza con cui un determinato consumatore dovrebbe acquistare un prodotto o un servizio da loro. Ciò aiuta le aziende a controllare l’inventario e ad assumere personale.
Risorse addizionali
Un’introduzione alla distribuzione normale
Un’introduzione alla distribuzione binomiale
Un’introduzione alla distribuzione di Poisson
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più