Distribuzione ipergeometrica

Di Benjamin anderson Agosto 6, 2023 Probabilità 0 commenti

In questo articolo spieghiamo cos’è la distribuzione ipergeometrica e come si calcola una probabilità con questo tipo di distribuzione. Troverai online la formula per la distribuzione ipergeometrica, quali sono le sue caratteristiche, nonché un calcolatore per calcolare la probabilità della distribuzione ipergeometrica.

Qual è la distribuzione ipergeometrica?

La distribuzione ipergeometrica è una distribuzione di probabilità che descrive il numero di casi di successo in un’estrazione casuale senza sostituzione di n elementi da una popolazione.

Cioè, la distribuzione ipergeometrica viene utilizzata per calcolare la probabilità di ottenere x successi estraendo n elementi da una popolazione senza sostituirne nessuno.

La distribuzione ipergeometrica ha tre parametri:

N : è il numero di elementi della popolazione (N = 0, 1, 2,…).
K : è il numero massimo di casi di successo (K = 0, 1, 2,…,N). Poiché in una distribuzione ipergeometrica un elemento può essere considerato solo un “successo” o un “fallimento”, NK è il numero massimo di casi di fallimento.
n : è il numero di recuperi senza sostituzione eseguiti.

$X \sim HG(N,K,n)$

Ad esempio, una variabile casuale discreta X che ha una distribuzione ipergeometrica con parametri N=8, K=5 e n=3 è definita come segue:

$X \sim HG(8,5,3)$

Formula di distribuzione ipergeometrica

La formula per la distribuzione ipergeometrica è il prodotto del numero combinatorio di K su x per il numero combinatorio di NK su nx diviso per il numero combinatorio di N su n .

Dove N è la dimensione della popolazione, K è il numero totale di casi favorevoli, n è il numero di estrazioni senza sostituzione e x è il numero di casi favorevoli per i quali deve essere calcolata la probabilità di accadimento.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la probabilità di un evento di una variabile che segue la distribuzione ipergeometrica.

Esempio di distribuzione ipergeometrica

Dopo aver visto la definizione e la formula della distribuzione ipergeometrica, ora risolveremo un esempio passo dopo passo in modo che tu sappia come calcolare la probabilità di una distribuzione ipergeometrica.

In un sacchetto mettiamo 20 palline blu e 30 palline rosse, cioè ci sono 50 palline in totale all’interno del sacchetto. Se estraiamo 12 palline senza sostituirne nessuna, calcola la probabilità di estrarre 4 palline blu.

La prima cosa da fare per risolvere l’esercizio è individuare i parametri della distribuzione ipergeometrica. In questo caso, il numero totale di elementi della popolazione è 50 ( N =50), il numero massimo di casi favorevoli è 20 ( K =20) e vengono estratte 12 palline ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Vogliamo calcolare la probabilità di estrarre 4 palline blu ( x =4), quindi applichiamo la formula della distribuzione ipergeometrica, sostituiamo le variabili con i loro valori corrispondenti ed eseguiamo il calcolo:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Calcolatore della distribuzione ipergeometrica

Inserisci i parametri della distribuzione ipergeometrica nel seguente calcolatore online per calcolare la probabilità che si verifichi l’evento desiderato.

Ricorda che N è la dimensione della popolazione, K è il numero totale di casi favorevoli, n è la dimensione del campione e x è il valore per il quale vogliamo trovare la probabilità che ciò accada.

Caratteristiche della distribuzione ipergeometrica

La distribuzione ipergeometrica ha le seguenti proprietà:

Il valore atteso di una distribuzione ipergeometrica è pari al numero di elementi del campione moltiplicato per il numero totale di casi favorevoli diviso per il numero di elementi della popolazione.

$E[X]=\cfrac{n\cdot K}{N}$

La modalità di una distribuzione ipergeometrica è il valore arrotondato per difetto dal prodotto di n+1 per K+1 diviso per N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

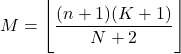
La varianza di una distribuzione ipergeometrica può essere ottenuta utilizzando la seguente espressione:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

La funzione generatrice dei momenti di una distribuzione ipergeometrica è la seguente:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

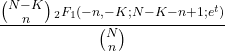
La funzione caratteristica della distribuzione ipergeometrica è la seguente:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

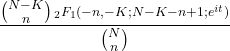
La probabilità che si verifichi un dato numero di eventi può essere calcolata dalla probabilità del numero precedente utilizzando la ricorsiva per la distribuzione ipergeometrica:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Distribuzione ipergeometrica e distribuzione binomiale

La differenza tra la distribuzione ipergeometrica e la distribuzione binomiale è la sostituzione. La distribuzione ipergeometrica viene utilizzata quando i recuperi non vengono sostituiti, tuttavia, nella distribuzione binomiale i recuperi vengono sostituiti.

Ad esempio, se peschiamo cinque carte a caso in un mazzo e vogliamo calcolare la probabilità di ottenere una determinata carta, se non sostituiamo ogni carta che peschiamo, dobbiamo utilizzare la distribuzione ipergeometrica per fare il calcolo. Ma se quando si rimuove una carta la si rimette a posto prima di eseguire l’estrazione successiva, allora bisogna utilizzare la distribuzione binomiale per calcolare la probabilità.

Quando il numero N è grande, il rapporto n/N è piccolo e il numero di casi favorevoli desiderati è molto piccolo, possiamo usare la distribuzione ipergeometrica come approssimazione della distribuzione binomiale. Lo sconsiglio però perché il risultato non sarà altrettanto attendibile e, inoltre, è più semplice calcolare le probabilità con la legge binomiale che con quella ipergeometrica.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più