Un'introduzione alla distribuzione multinomiale

La distribuzione multinomiale descrive la probabilità di ottenere un numero specifico di conteggi per k risultati diversi, quando ciascun risultato ha una probabilità fissa di verificarsi.

_{Se una} variabile casuale _{_} può essere trovata con la seguente formula:

Probabilità = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

Oro:

• n: numero totale di eventi
• x ₁ : numero di volte in cui si verifica il risultato 1
• p ₁ : probabilità che si verifichi il risultato 1 in una data prova

Ad esempio, supponiamo che in un’urna ci siano 5 biglie rosse, 3 biglie verdi e 2 biglie blu. Se estraiamo a caso 5 biglie dall’urna, con reinserimento, qual è la probabilità di ottenere esattamente 2 biglie rosse, 2 biglie verdi e 1 biglia blu?

Per rispondere a questa domanda possiamo utilizzare la distribuzione multinomiale con i seguenti parametri:

• n : 5
• x ₁ (# biglie rosse) = 2, x ₂ (# biglie verdi) = 2, x ₃ (# biglie blu) = 1
• p ₁ (probabilità rossa) = 0,5, p ₂ (probabilità verde) = 0,3, p ₃ (probabilità blu) = 0,2

Inserendo questi numeri nella formula, troviamo che la probabilità è:

Probabilità = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Problemi pratici di distribuzione multinomiale

Utilizza i seguenti problemi pratici per verificare la tua conoscenza della distribuzione multinomiale.

Nota: utilizzeremo il calcolatore della distribuzione multinomiale per calcolare le risposte a queste domande.

Problema 1

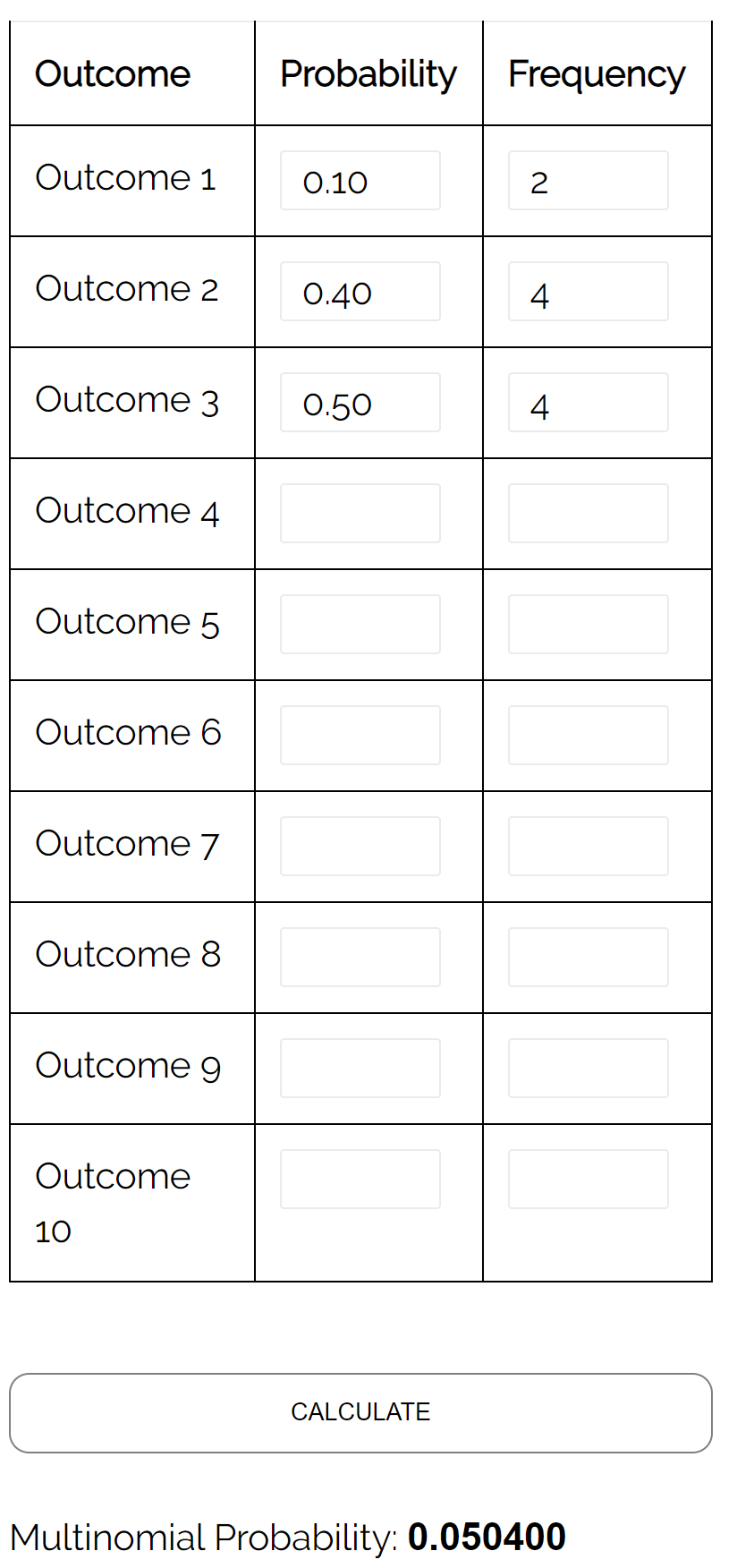
Domanda: In un’elezione a sindaco a tre, il candidato A riceve il 10% dei voti, il candidato B riceve il 40% dei voti e il candidato C riceve il 50% dei voti. Se selezioniamo un campione casuale di 10 elettori, qual è la probabilità che 2 abbiano votato per il candidato A, 4 abbiano votato per il candidato B e 4 abbiano votato per il candidato C?

Risposta: Utilizzando il calcolatore della distribuzione multinomiale con i seguenti input, troviamo che la probabilità è 0,0504:

Problema 2

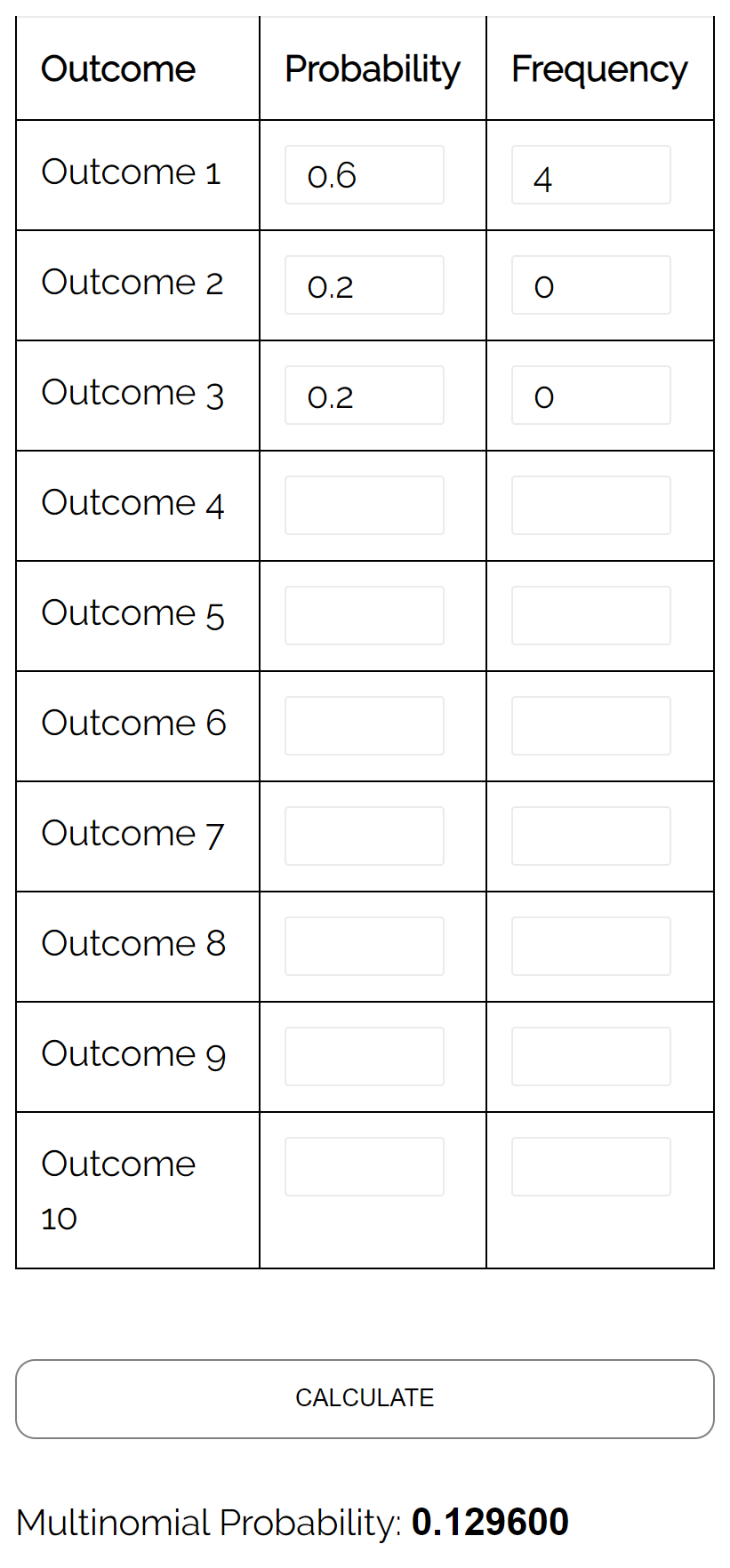
Domanda: Supponiamo che un’urna contenga 6 biglie gialle, 2 biglie rosse e 2 biglie rosa. Se estraiamo a caso 4 palline dall’urna, con reinserimento, qual è la probabilità che tutte e 4 le palline siano gialle?

Risposta: Utilizzando il calcolatore della distribuzione multinomiale con i seguenti input, troviamo che la probabilità è 0,1296:

Problema 3

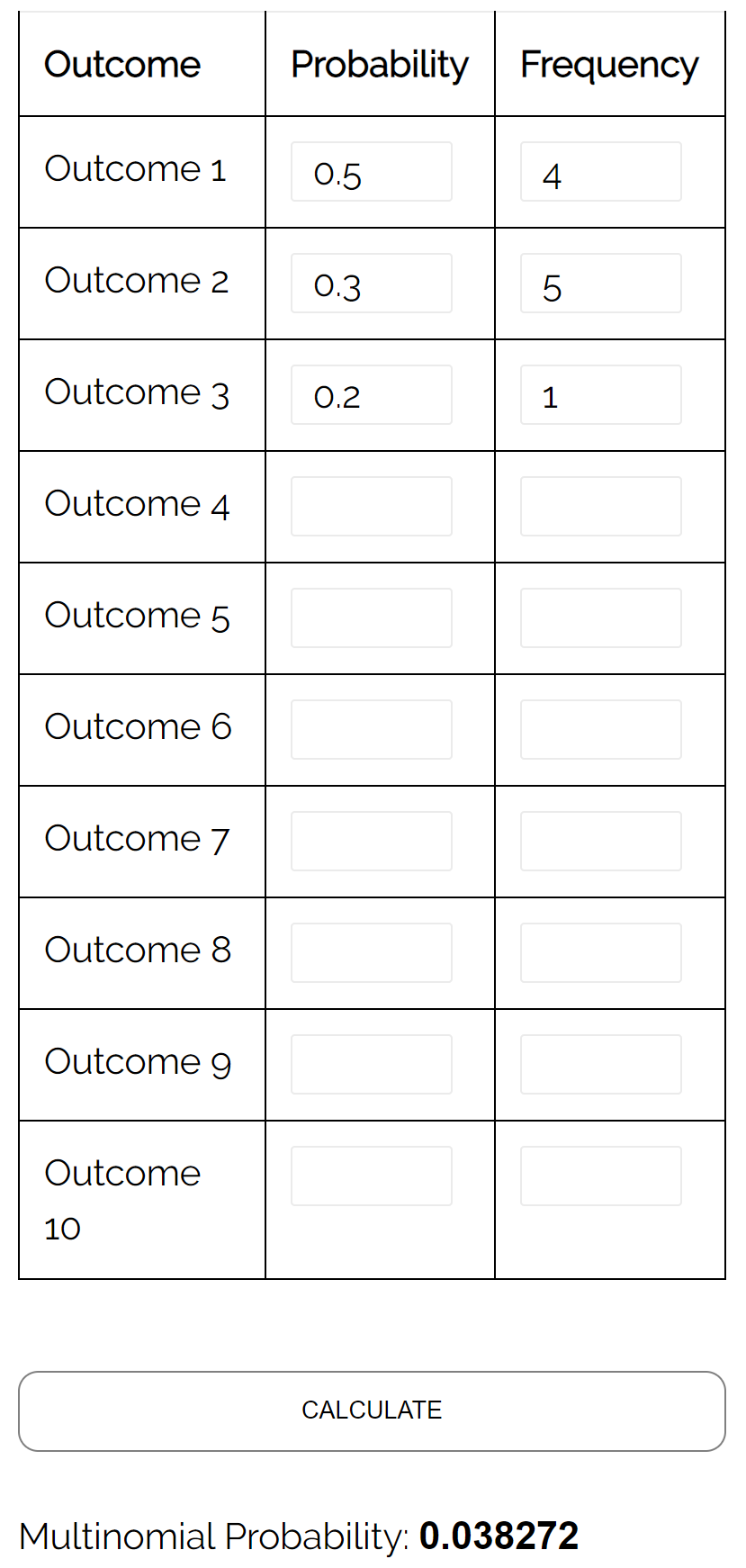
Domanda: Supponiamo che due studenti stiano giocando a scacchi l’uno contro l’altro. La probabilità che lo studente A vinca un dato gioco è 0,5, la probabilità che lo studente B vinca un dato gioco è 0,3 e la probabilità che ci sia un pareggio in un dato gioco è 0,2. Se giocano 10 giochi, qual è la probabilità? probabilità che il giocatore A vinca 4 volte, il giocatore B vinca 5 volte e che pareggiano 1 volta?

Risposta: utilizzando il calcolatore della distribuzione multinomiale con i seguenti input, troviamo che la probabilità è 0,038272:

Risorse addizionali

I seguenti tutorial forniscono un’introduzione ad altre distribuzioni comuni nelle statistiche:

Un’introduzione alla distribuzione normale
Un’introduzione alla distribuzione binomiale
Un’introduzione alla distribuzione di Poisson
Un’introduzione alla distribuzione geometrica