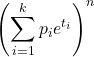Distribuzione multinomiale

Di Benjamin anderson Agosto 4, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è una distribuzione multinomiale nelle statistiche. Troverai quindi la definizione di distribuzione multinomiale, qual è la sua formula, un esercizio risolto e quali sono le proprietà di questo tipo di distribuzione di probabilità. Inoltre, potrai calcolare la probabilità di una distribuzione multinomiale con un calcolatore online.

Cos’è una distribuzione multinomiale?

La distribuzione multinomiale (o distribuzione multinomiale ) è una distribuzione di probabilità che descrive la probabilità che più eventi mutuamente esclusivi si verifichino un dato numero di volte dopo diverse prove.

Cioè, se un esperimento casuale può dare come risultato tre o più eventi esclusivi ed è nota la probabilità che ciascun evento si verifichi separatamente, la distribuzione multinomiale viene utilizzata per calcolare la probabilità che quando vengono eseguiti più esperimenti si verifichi un certo numero di eventi. volta ogni volta.

La distribuzione multinomiale è quindi una generalizzazione della distribuzione binomiale.

Formula di distribuzione multinomiale

Per calcolare una probabilità di distribuzione multinomiale, è necessario innanzitutto determinare il quoziente tra il fattoriale del numero totale di dati e i fattoriali del numero di occorrenze di ciascun evento, e il risultato viene moltiplicato per il prodotto della probabilità di ciascun evento. portato al numero di occorrenze di detto evento.

In altre parole, la formula per la distribuzione multinomiale è la seguente:

Oro:

$P$

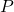
è la probabilità della distribuzione multinomiale calcolata.
$n$

è il numero totale di test eseguiti.
$x_i$

è il numero di volte in cui si verifica l’evento

$i$

.
$p_i$

è la probabilità che l’evento si verifichi

$i$

.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la probabilità di una variabile che segue la distribuzione multinomiale.

Esempio di distribuzione multinomiale

Per finire di comprendere il concetto di distribuzione multinomiale, di seguito hai risolto un esempio di calcolo della probabilità di una distribuzione multinomiale.

Un negozio vende tre prodotti diversi. Quando un cliente effettua un acquisto, la probabilità che si tratti del prodotto A, del prodotto B o del prodotto C è rispettivamente del 30%, 15% e 55%. Trovare la probabilità che quando il negozio ha venduto 8 unità, 2 siano del prodotto A, 1 del prodotto B e 5 del prodotto C.

Il problema definito è governato da una distribuzione multinomiale, è quindi necessario applicare la formula per questo tipo di distribuzione di probabilità:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

Quindi sostituiamo i dati del problema nella formula ed eseguiamo il calcolo della probabilità:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

Quindi la probabilità che ciò che viene affermato nella dichiarazione del problema accada è dell’11,4%.

Calcolatore della distribuzione multinomiale

Scrivi il numero di occorrenze di ciascun evento nella prima casella e, nello stesso ordine, la probabilità che si verifichi ogni evento nella seconda casella. Quindi inserisci il numero totale di tentativi effettuati nell’ultimo spazio vuoto.

I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Proprietà della distribuzione multinomiale

La distribuzione multinomiale ha le seguenti caratteristiche:

In una distribuzione multinomiale, il valore atteso del numero di volte in cui si verifica l’evento i quando si eseguono n prove è uguale al numero totale di prove eseguite moltiplicato per la probabilità che si verifichi l’evento.

$E[x_i]=n\cdot p_i$

In una distribuzione multinomiale, la varianza dell’evento i viene calcolata utilizzando la seguente espressione:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

Allo stesso modo, la covarianza tra due eventi è equivalente al prodotto del numero totale di prove moltiplicato per la probabilità di ciascun evento moltiplicata per -1:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

La funzione generatrice dei momenti per una distribuzione multinomiale è:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più