Distribuzione normale

Questo articolo spiega qual è la distribuzione normale nelle statistiche. Quindi troverai la definizione di distribuzione normale, esempi di distribuzioni normali e quali sono le proprietà della distribuzione normale.

Qual è la distribuzione normale?

La distribuzione normale è una distribuzione di probabilità continua il cui grafico è a campana e simmetrico rispetto alla sua media. In statistica, la distribuzione normale viene utilizzata per modellare fenomeni con caratteristiche molto diverse, motivo per cui questa distribuzione è così importante.

Infatti, in statistica, la distribuzione normale è considerata di gran lunga la più importante tra tutte le distribuzioni di probabilità, perché non solo può modellare un gran numero di fenomeni del mondo reale, ma può anche essere utilizzata per approssimare altri tipi di fenomeni. distribuzioni. a determinate condizioni.

Il simbolo della distribuzione normale è la lettera maiuscola N. Quindi, per indicare che una variabile segue una distribuzione normale, si indica con la lettera N e si aggiungono tra parentesi i valori della sua media aritmetica e della deviazione standard.

La distribuzione normale ha molti nomi diversi, tra cui distribuzione gaussiana , distribuzione gaussiana e distribuzione di Laplace-Gauss .

Esempi di distribuzioni normali

In genere, i set di dati che seguono una distribuzione normale contengono un gran numero di osservazioni e coprono argomenti molto generali. Di seguito sono riportati alcuni esempi di campioni statistici che generalmente possono essere modellati con una distribuzione normale.

Esempi di distribuzione normale:

1. La dimensione degli studenti in un corso.
2. Il QI dei lavoratori di un’azienda.
3. Il numero di parti difettose prodotte in una fabbrica in un giorno.
4. I voti ottenuti in un esame dagli studenti di un corso.
5. La redditività delle azioni delle società quotate in borsa.

Grafico della distribuzione normale

Dopo aver visto cos’è la distribuzione normale e alcuni esempi di questo tipo di distribuzione di probabilità, vediamo come si presenta il suo grafico per comprendere meglio il concetto.

Nel grafico seguente puoi vedere come varia la funzione di densità della distribuzione normale a seconda dei valori della sua media aritmetica e della deviazione standard.

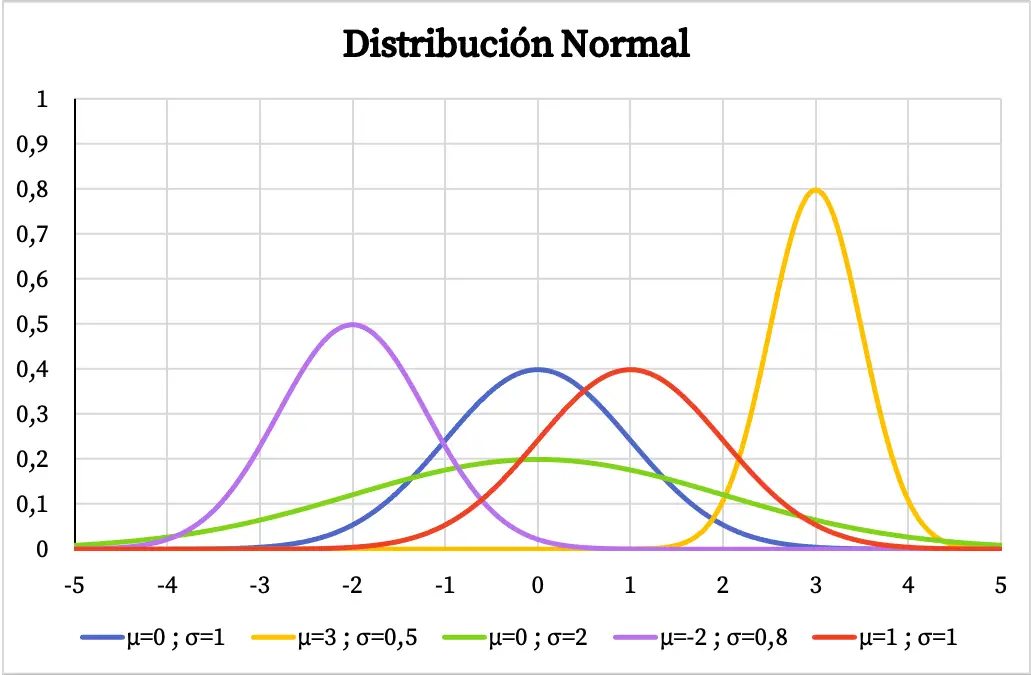
Avendo una forma a campana centrata sulla media aritmetica, se una variabile ha una distribuzione normale significa che il valore più ripetuto è la media e che i valori attorno alla media si ripetono più frequentemente rispetto ai valori estremi. Allo stesso modo, maggiore è la deviazione standard della distribuzione normale, più piatta è la forma della sua rappresentazione grafica.

D’altra parte, il grafico della funzione di probabilità cumulativa della distribuzione normale dipende anche dai valori della sua media aritmetica e della deviazione standard, come puoi vedere nell’immagine seguente:

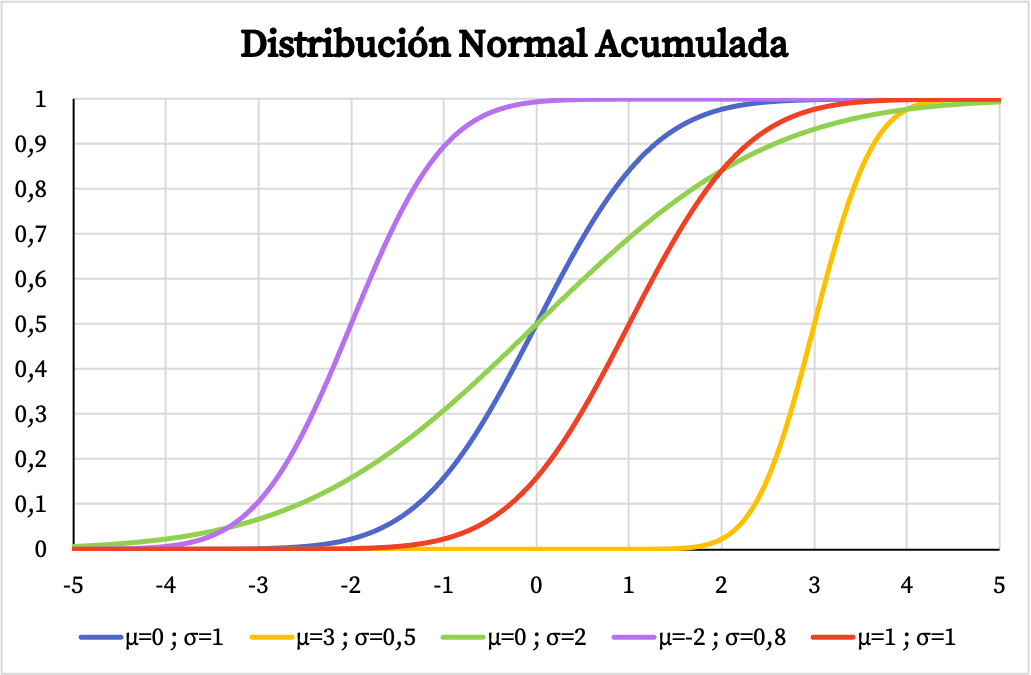
La funzione di densità e la funzione di distribuzione della distribuzione normale permettono di calcolare le probabilità legate a questa distribuzione. Tuttavia, invece di utilizzare le loro formule, puoi utilizzare direttamente le normali tabelle di distribuzione perché è più veloce. È possibile consultare tali tabelle al seguente link:

Caratteristiche della distribuzione normale

La distribuzione normale ha le seguenti caratteristiche:

• La distribuzione normale dipende da due parametri caratteristici, che sono la media aritmetica (μ) e la deviazione standard (σ).

• La distribuzione normale può assumere valori positivi e negativi, quindi il dominio della distribuzione normale è costituito da numeri reali.

• La mediana e la moda della distribuzione normale sono uguali alla media aritmetica della distribuzione.

• Il coefficiente di asimmetria e il coefficiente di curtosi della distribuzione normale sono zero.

• La formula per la funzione di densità della distribuzione normale è:

• Allo stesso modo, la formula per la funzione di probabilità cumulativa della distribuzione normale è:

• Un’applicazione del teorema del limite centrale è che una distribuzione di Poisson può approssimare una distribuzione normale quando il valore di λ è sufficientemente grande.

• Un’altra applicazione del teorema del limite centrale è che una distribuzione binomiale può essere approssimata da una distribuzione normale per insiemi di dati con un gran numero di osservazioni.

Distribuzione normale standardizzata

La distribuzione normale standard , detta anche distribuzione normale unitaria , è il caso più semplice di distribuzione normale. Più precisamente, la distribuzione normale standard è una distribuzione normale con valori di media e deviazione standard pari rispettivamente a 0 e 1.

Si noti che qualsiasi distribuzione normale può essere trasformata in una distribuzione normale standard applicando un processo chiamato tipizzazione, che prevede la sottrazione della media aritmetica da ciascun valore e la divisione per la deviazione standard.

Inoltre, la distribuzione normale standard viene utilizzata per determinare qualsiasi probabilità di una distribuzione normale utilizzando la sua tabella di probabilità. Quindi, per trovare la probabilità di una distribuzione normale, viene prima inserita la variabile per convertirla in una distribuzione normale standard e, quindi, si guarda nella tabella per vedere qual è il valore di probabilità corrispondente. Per saperne di più clicca sul seguente link:

La distribuzione normale e la regola empirica

In statistica, la regola pratica , chiamata anche regola 68-95-99.7 , è una regola che definisce la percentuale di valori in una distribuzione normale che rientrano in tre deviazioni standard della media.

Più nello specifico, la regola pratica prevede quanto segue:

• Il 68% dei valori in una distribuzione normale si trova entro una deviazione standard dalla media.
• Il 95% dei valori in una distribuzione normale si trovano entro due deviazioni standard dalla media.
• Il 99,7% dei valori in una distribuzione normale rientrano nelle tre deviazioni standard della media.