Come simulare e tracciare una distribuzione normale bivariata in r

In statistica, due variabili seguono una distribuzione normale bivariata se hanno una distribuzione normale quando vengono sommate.

Questo tutorial spiega come eseguire le seguenti attività in R:

• Simulare una distribuzione normale bivariata
• Tracciare una distribuzione normale bivariata utilizzando un diagramma di contorno (diagramma 2D)
• Tracciare una distribuzione normale bivariata utilizzando un grafico di superficie (grafico 3D)

Andiamo!

Esempio 1: simulare una distribuzione normale bivariata in R

Il modo più semplice per simulare una distribuzione normale bivariata in R è utilizzare la funzione mvrnorm() del pacchetto MASS .

Il codice seguente mostra come utilizzare questa funzione per simulare nella pratica una distribuzione normale bivariata:

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

Ecco cosa fa ogni argomento della funzione mvrnorm() :

• n : definisce la dimensione del campione
• mu : Definisce la media di ciascuna variabile
• Sigma : Definisce la matrice di covarianza delle due variabili

Il risultato finale è un frame di dati con due variabili che seguono una distribuzione normale quando sommate.

Esempio 2: tracciare una distribuzione normale bivariata

Il modo più semplice per tracciare una distribuzione normale bivariata in R è utilizzare le funzioni nel pacchetto mnormt() .

Ad esempio, possiamo utilizzare la funzione contour() di questo pacchetto per creare un diagramma di contorno, che fornisce una visualizzazione 2D della distribuzione normale bivariata:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

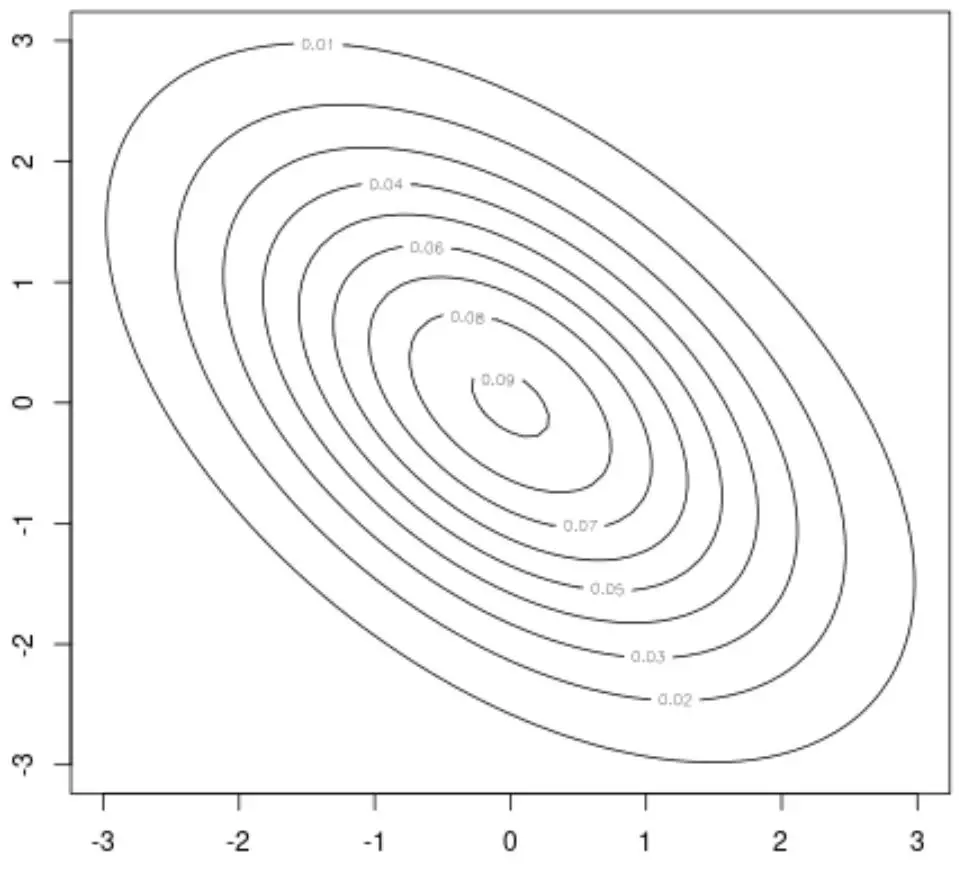
Possiamo anche utilizzare la funzione persp() per creare un grafico di superficie, che fornisce una visualizzazione 3D della distribuzione normale bivariata:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

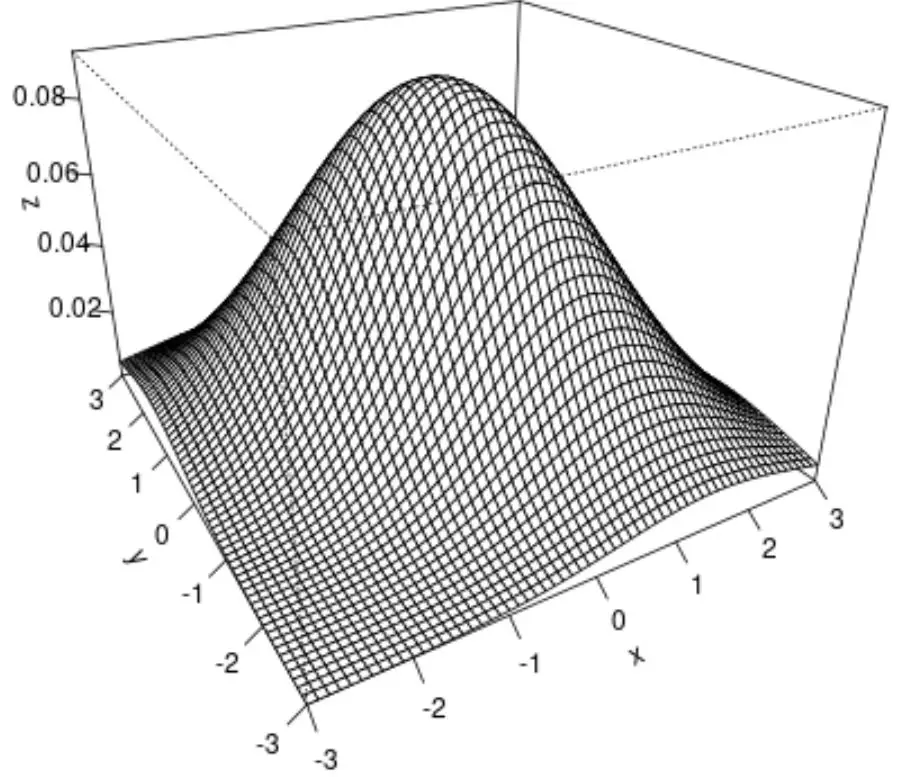
Ecco cosa fa ogni argomento della funzione persp() :

• theta, phi : imposta gli angoli di direzione della visualizzazione.
• espandere : controlla la dimensione dell’asse z.
• ticktype : controlla l’aspetto dei segni di spunta sugli assi.

Il risultato finale è un grafico di superficie 3D della distribuzione normale bivariata.

Risorse addizionali

I seguenti tutorial spiegano come utilizzare altre distribuzioni di probabilità in R:

Come utilizzare la distribuzione normale in R
Come utilizzare la distribuzione binomiale in R
Come utilizzare la distribuzione di Poisson in R
Come utilizzare la distribuzione multinomiale in R