Distribuzione normale inversa: definizione ed esempio

Il termine distribuzione normale inversa si riferisce al metodo di utilizzo di una probabilità nota per trovare il corrispondente valore z-critico in una distribuzione normale .

Questa non deve essere confusa con la distribuzione gaussiana inversa , che è una distribuzione di probabilità continua.

Questo tutorial fornisce diversi esempi di utilizzo della distribuzione normale inversa in diversi software statistici.

Distribuzione normale inversa abbiamo la calcolatrice TI-83 o TI-84

È molto probabile che incontrerai il termine “distribuzione normale inversa” su una calcolatrice TI-83 o TI-84, che utilizza la seguente funzione per trovare il valore z critico che corrisponde a una certa probabilità:

invNorm(probabilità, μ, σ)

Oro:

• probabilità: il livello di significatività
• μ: media della popolazione
• σ: deviazione standard della popolazione

È possibile accedere a questa funzione su una calcolatrice TI-84 premendo 2nd quindi premendo vars . Questo ti porterà a una schermata DISTR dove potrai quindi utilizzare invNorm() :

Ad esempio, possiamo utilizzare questa funzione per trovare il valore z-critico che corrisponde a un valore di probabilità di 0,05:

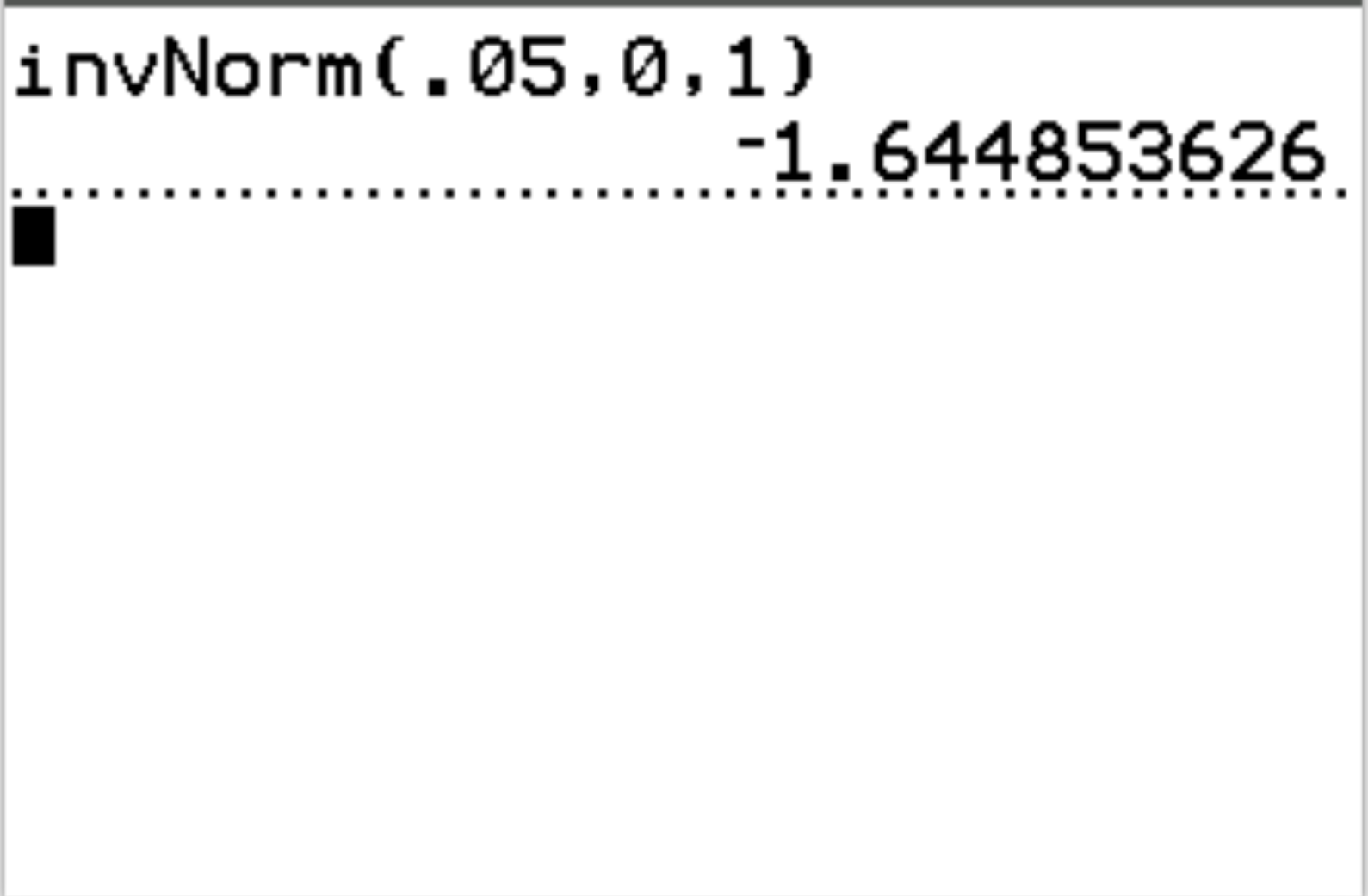
Il valore z critico che corrisponde a un valore di probabilità di 0,05 è -1,64485 .

Correlato: Come utilizzare invNorm su una calcolatrice TI-84 (con esempi)

Distribuzione normale inversa in Excel

Per trovare il valore z-critico associato a un determinato valore di probabilità in Excel, possiamo utilizzare la funzione INVNORM() , che utilizza la seguente sintassi:

INVNORM(p, media, sd)

Oro:

• p: il livello di significatività
• media: media della popolazione
• ds: deviazione standard della popolazione

Ad esempio, possiamo utilizzare questa funzione per trovare il valore z-critico che corrisponde a un valore di probabilità di 0,05:

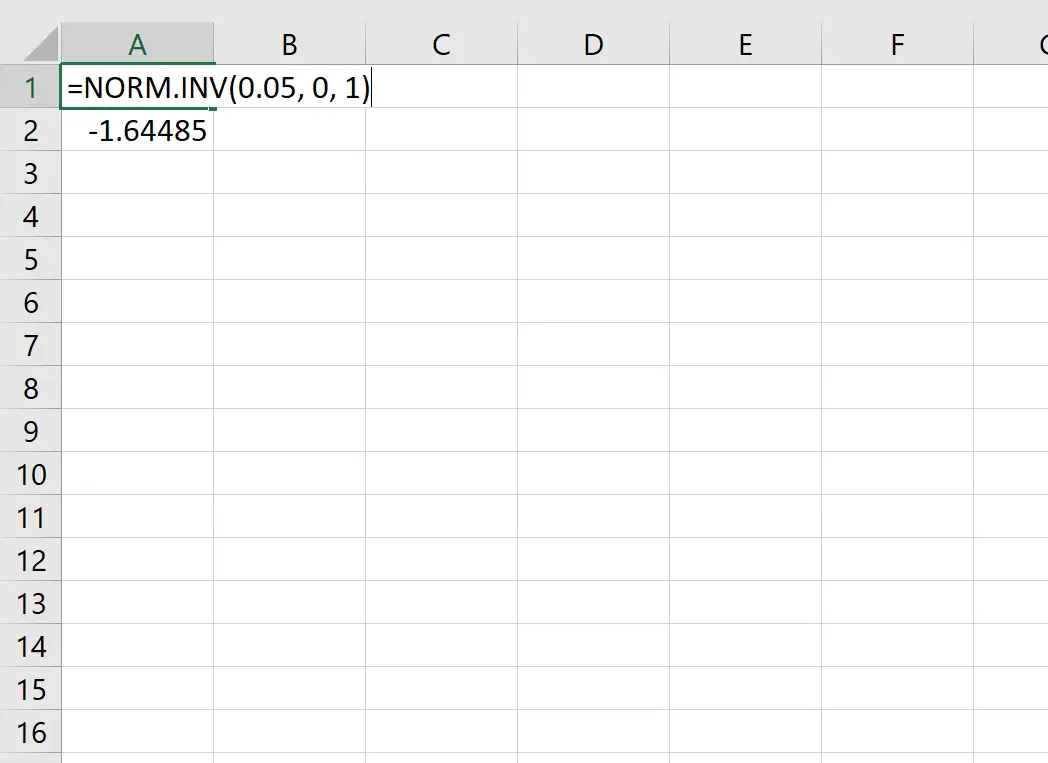
Il valore z critico che corrisponde a un valore di probabilità di 0,05 è -1,64485 .

Distribuzione normale inversa in R

Per trovare il valore z-critico associato ad un certo valore di probabilità in R, possiamo utilizzare la funzioneqnorm() , che utilizza la seguente sintassi:

qnorm (p, media, sd)

Oro:

• p: il livello di significatività
• media: media della popolazione
• ds: deviazione standard della popolazione

Ad esempio, possiamo utilizzare questa funzione per trovare il valore z-critico che corrisponde a un valore di probabilità di 0,05:

 qnorm (p= .05 , mean= 0 , sd= 1 )

[1] -1.644854

Ancora una volta, il valore z critico che corrisponde a un valore di probabilità di 0,05 è -1,64485 .