Distribuzione normale e distribuzione normale standardizzata: la differenza

La distribuzione normale è la distribuzione di probabilità più comunemente utilizzata in statistica.

Ha le seguenti proprietà:

• Simmetrico
• A forma di campana
• La media e la mediana sono uguali; entrambi situati al centro della distribuzione

La media della distribuzione normale determina la sua posizione e la deviazione standard ne determina la diffusione.

Ad esempio, il grafico seguente mostra tre distribuzioni normali con medie e deviazioni standard diverse:

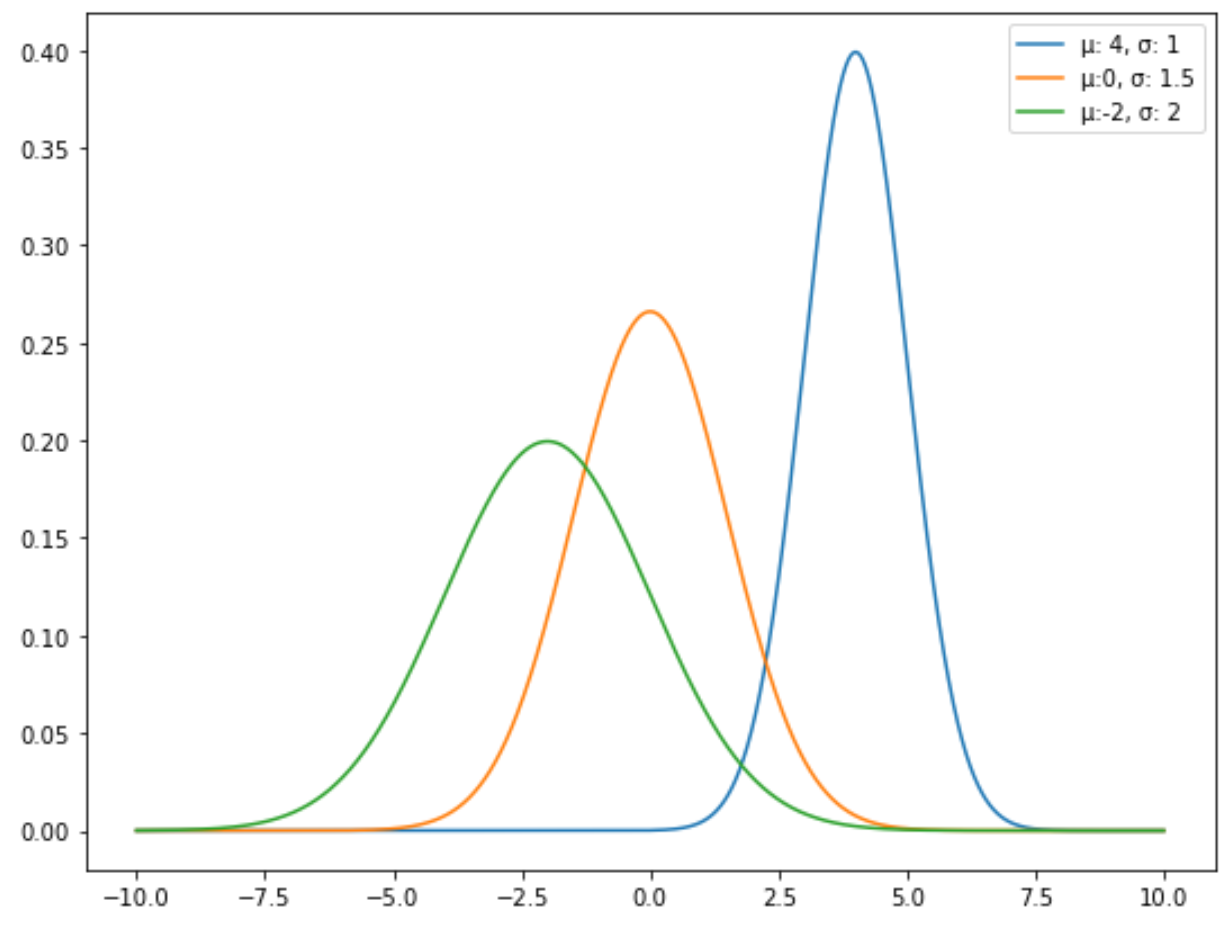
La distribuzione normale standard è un tipo specifico di distribuzione normale in cui la media è 0 e la deviazione standard è 1.

Il grafico seguente mostra una distribuzione normale standard:

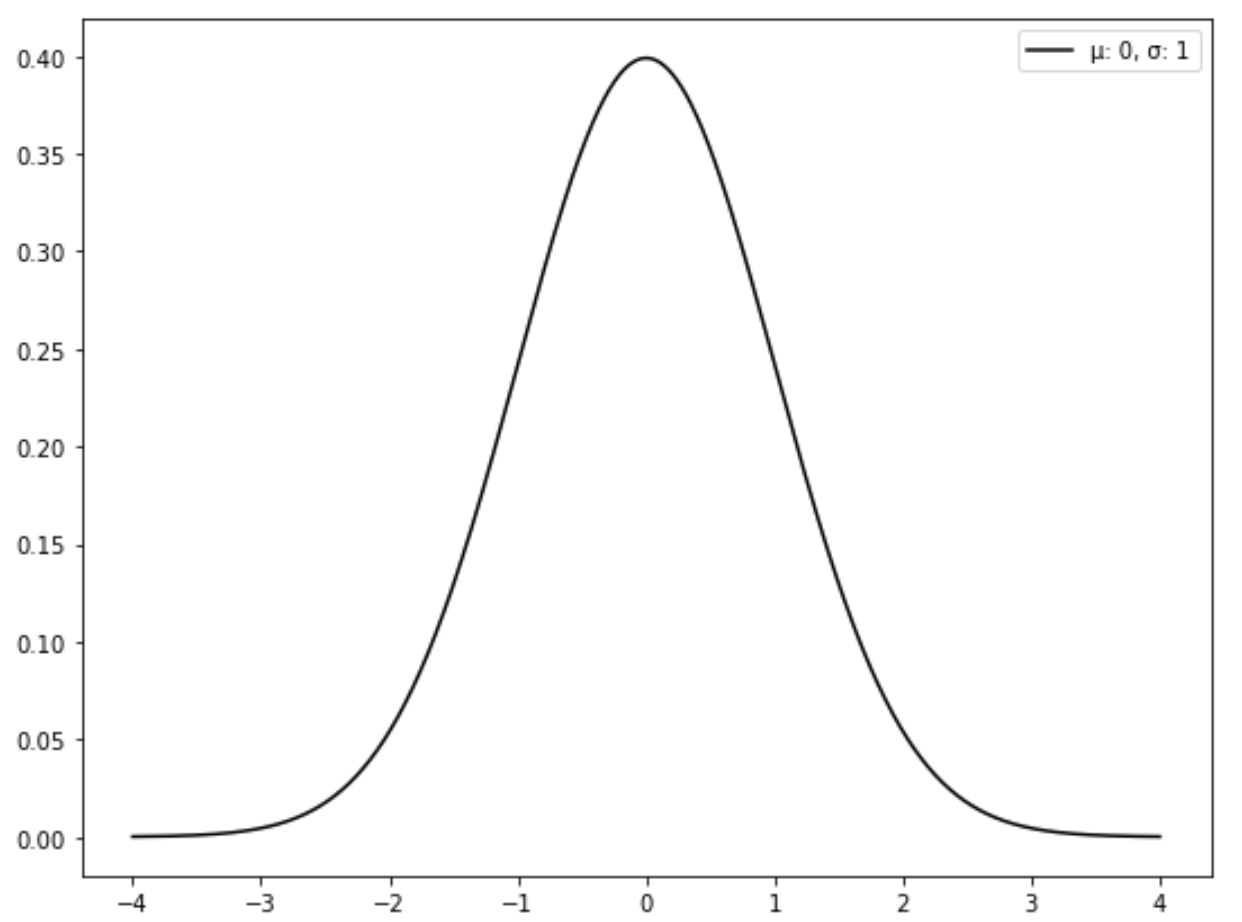
Come convertire una distribuzione normale in una distribuzione normale standard

Qualsiasi distribuzione normale può essere convertita in una distribuzione normale standard convertendo i valori dei dati in punteggi z, utilizzando la seguente formula:

z = (x – μ) / σ

Oro:

• x: valore del singolo dato
• μ: Media della distribuzione
• σ: deviazione standard della distribuzione

Ad esempio, supponiamo di avere il seguente set di dati con una media di 6 e una deviazione standard di 2.152:

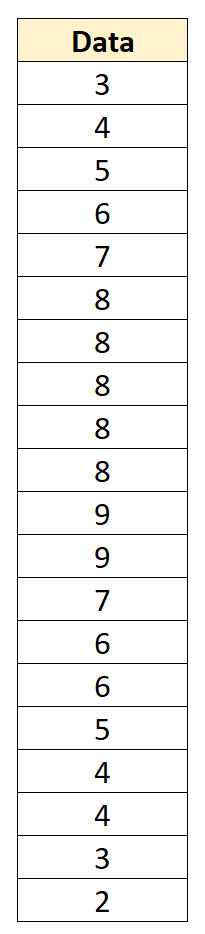
Possiamo convertire ogni singolo valore di dati in un punteggio z sottraendo 6 da ciascun valore e dividendo per 2,152:

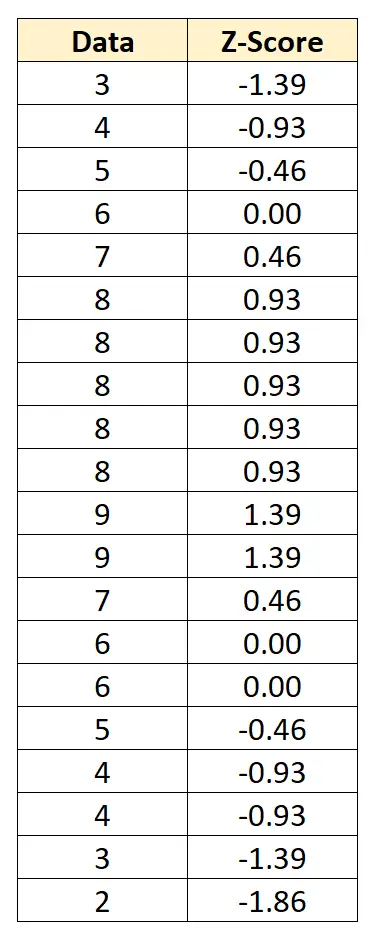
Il punteggio z ci dice quante deviazioni standard ha ogni punto dati dalla media. Ad esempio, il primo valore dei dati “3” è 1,39 deviazioni standard sotto la media.

La media di questa distribuzione dei punteggi ha una media pari a zero e una deviazione standard pari a uno.

Come utilizzare la distribuzione normale standardizzata

Una distribuzione normale standard ha le seguenti proprietà:

• Circa il 68% dei dati rientra in una deviazione standard della media
• Circa il 95% dei dati rientra nelle due deviazioni standard della media.
• Circa il 99,7% dei dati rientra nelle tre deviazioni standard della media.

Questa è nota come regola pratica e viene utilizzata per comprendere la distribuzione dei valori in un set di dati.

Ad esempio, supponiamo che l’altezza delle piante in un determinato giardino sia distribuita normalmente con una media di 47,4 pollici e una deviazione standard di 2,4 pollici.

Utilizzando la regola pratica, quale percentuale di piante è alta meno di 54,6 pollici?

La regola pratica afferma che per un dato set di dati con una distribuzione normale, il 99,7% dei valori dei dati rientra in tre deviazioni standard della media. Ciò significa che il 49,85% dei valori rientra tra la media e tre deviazioni standard sopra la media.

In questo esempio, 54,6 corrisponde a tre deviazioni standard sopra la media. Poiché sappiamo che il 50% dei valori dei dati è inferiore alla media in una distribuzione normale, un totale di 50% + 49,85% = 99,85% dei valori è inferiore a 54,6.

Quindi il 99,85% delle piante sono alte meno di 54,6 pollici.

Risorse addizionali

Problemi nel mettere in pratica le regole pratiche
Calcolatore delle regole del pollice
Come applicare la regola pratica in Excel