Distribuzione normale e distribuzione t: qual è la differenza?

La distribuzione normale è la distribuzione più comunemente utilizzata in tutte le statistiche ed è nota per essere simmetrica e a forma di campana.

Una distribuzione strettamente correlata è la distribuzione t , anch’essa simmetrica e a forma di campana ma con “code” più pesanti della distribuzione normale.

In altre parole, nella distribuzione si trovano più valori alle estremità che al centro rispetto alla distribuzione normale:

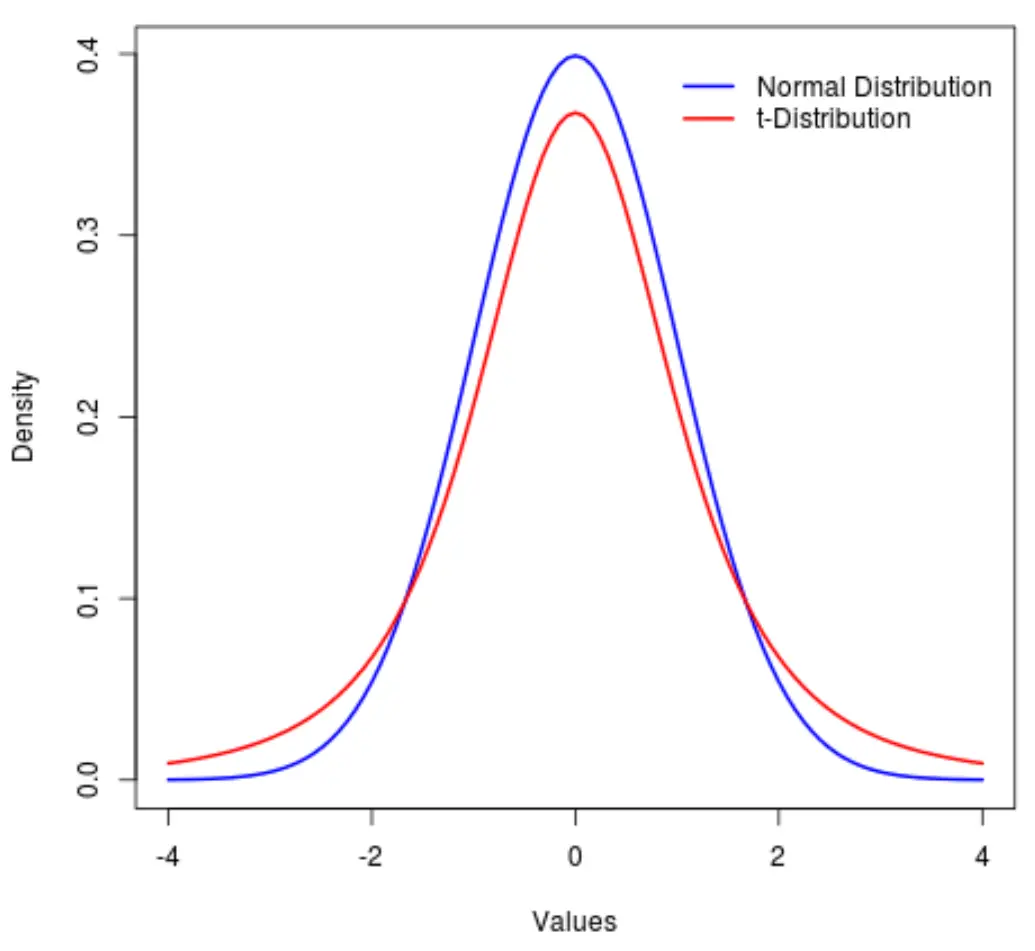
Nel gergo statistico, utilizziamo una metrica chiamata curtosi per misurare quanto sia “pesante” una distribuzione. Quindi, diremmo che la curtosi di una distribuzione t è maggiore di quella di una distribuzione normale.

In pratica, utilizziamo molto spesso la distribuzione t quando eseguiamo test di ipotesi o costruiamo intervalli di confidenza .

Ad esempio, la formula per calcolare un intervallo di confidenza per la media della popolazione è:

Intervallo di confidenza = x +/- t _{1-α/2, n-1} *(s/√ n )

Oro:

• x : mezzi campione
• t: il valore t critico, basato sul livello di significatività α e sulla dimensione del campione n
• s: deviazione standard campionaria
• n: dimensione del campione

In questa formula utilizziamo il valore critico della tabella t invece del valore critico della tabella z quando è vera una delle seguenti condizioni:

• Non conosciamo la deviazione standard della popolazione.
• La dimensione del campione è inferiore o uguale a 30.

Il seguente diagramma di flusso fornisce un modo utile per sapere se è necessario utilizzare il valore critico della tabella t o della tabella z:

La differenza principale tra l’utilizzo della distribuzione t e l’utilizzo della distribuzione normale quando si costruiscono intervalli di confidenza è che i valori critici della distribuzione t saranno maggiori, portando a intervalli di confidenza più ampi .

Ad esempio, supponiamo di voler costruire un intervallo di confidenza al 95% per il peso medio di una popolazione di tartarughe, al fine di raccogliere un campione casuale di tartarughe con le seguenti informazioni:

• Dimensione del campione n = 25
• Peso medio del campione x = 300
• Deviazione standard del campione s = 18,5

Il valore z critico per un livello di confidenza del 95% è 1,96 mentre un valore t critico per un intervallo di confidenza del 95% con df = 25-1 = 24 gradi di libertà è 2,0639 .

Pertanto, un intervallo di confidenza al 95% per la media della popolazione utilizzando un valore z-critico è:

IC al 95% = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

Mentre un intervallo di confidenza del 95% per la media della popolazione utilizzando un valore t-critico è:

IC al 95% = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Si noti che l’intervallo di confidenza con il valore t-critico è più ampio.

L’idea qui è che quando abbiamo campioni di piccole dimensioni siamo meno sicuri della media reale della popolazione, quindi è utile utilizzare la distribuzione t per produrre intervalli di confidenza più ampi che abbiano maggiori possibilità di contenere la media reale della popolazione.

Visualizzazione dei gradi di libertà della distribuzione t

È opportuno notare che all’aumentare dei gradi di libertà la distribuzione t si avvicina alla distribuzione normale.

Per illustrare ciò, si consideri il grafico seguente che mostra la forma della distribuzione t con i seguenti gradi di libertà:

• df = 3
• df = 10
• df = 30

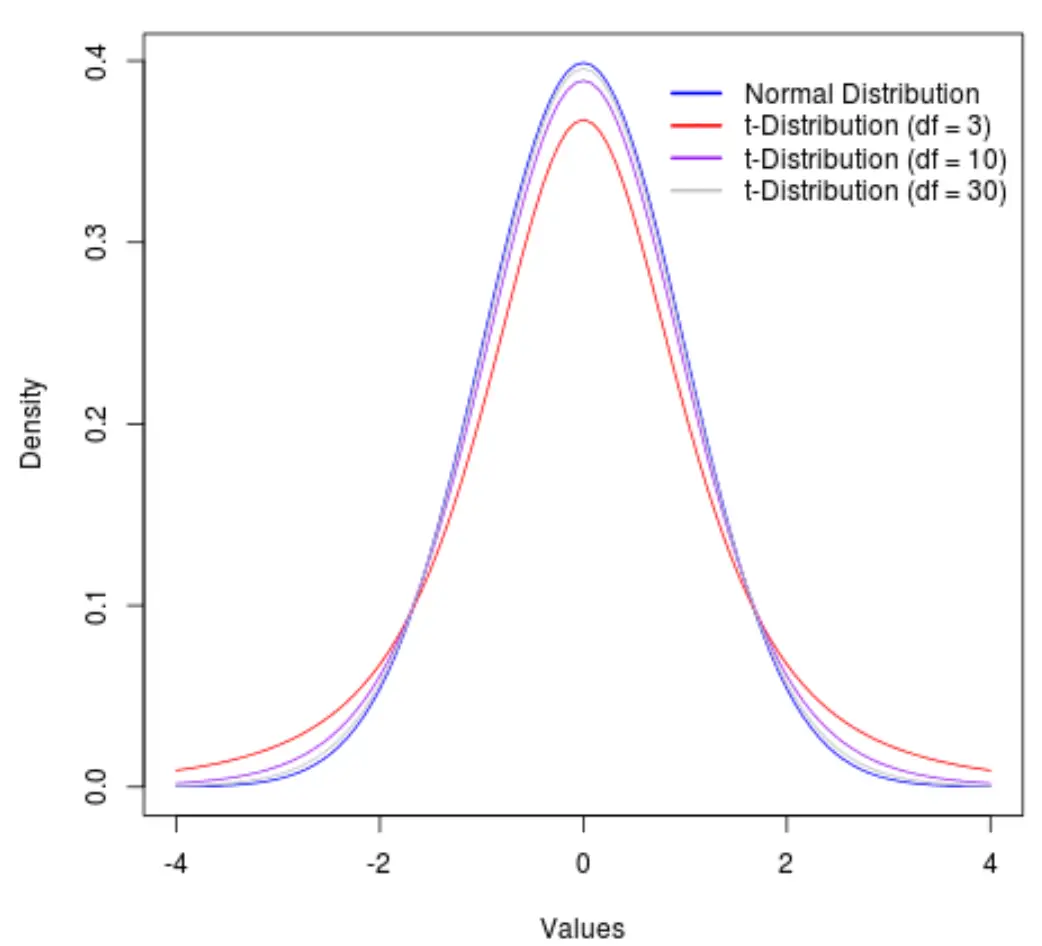
Oltre i 30 gradi di libertà, la distribuzione t e la distribuzione normale diventano così simili che le differenze tra l’utilizzo di un valore critico t e un valore critico z nelle formule diventano trascurabili.